Carnot syklus stadier, applikasjoner, eksempler, øvelser

De Carnot syklus det er sekvensen av termodynamiske prosesser som finner sted i en Carnot-motor, en ideell enhet som bare består av reversible typeprosesser; det vil si de som har funnet sted, kan gå tilbake til opprinnelig tilstand.

Denne typen motor anses som ideell, siden den mangler spredning, friksjon eller viskositet som oppstår i virkelige maskiner, og omdanner termisk energi til brukbart arbeid, selv om konverteringen ikke utføres 100%.

En motor er bygget med utgangspunkt i et stoff som er i stand til å utføre arbeid, for eksempel gass, bensin eller damp. Dette stoffet blir utsatt for forskjellige temperaturendringer og opplever i sin tur variasjoner i trykk og volum. På denne måten er det mulig å flytte et stempel inne i en sylinder.

Artikkelindeks

• 1 Hva er carnot-syklusen?
• 2 trinn i Carnot-syklusen
  • 2.1 Utgangspunkt
  • 2.2 Første trinn: isoterm ekspansjon
  • 2.3 Andre trinn: adiabatisk utvidelse
  • 2.4 Tredje trinn: isoterm kompresjon
  • 2.5 Fjerde trinn: adiabatisk kompresjon
• 3 Carnots teorem
  • 3.1 Bevis på Carnots teorem
  • 3.2 Resultat av teorem og begrensninger
• 4 Eksempler
  • 4.1 Et stempel inne i en sylinder
  • 4.2 Ulike reversible prosesser
  • 4.3 Et atomkraftverk
• 5 Øvelser løst
  • 5.1-Eksempel 1: effektivitet til en varmemotor
  • 5.2-Eksempel 2: absorbert varme og varmeoverført
• 6 Referanser

Hva er carnot-syklusen?

Carnot-syklusen foregår i et system kalt Carnot-motoren eller C, som er en ideell gass innesluttet i en sylinder og utstyrt med et stempel som er i kontakt med to kilder ved forskjellige temperaturer T₁ og T_to som den som er vist i figuren nedenfor til venstre.

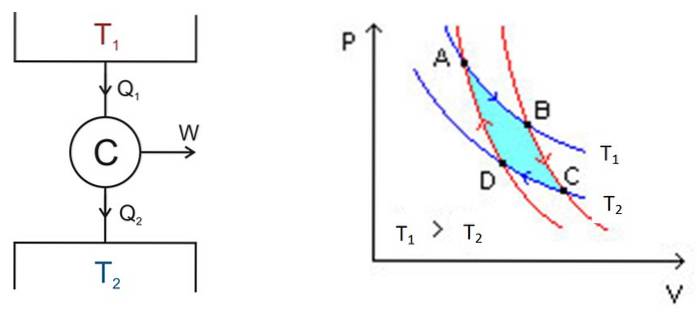
Der foregår følgende grove prosesser:

1. En viss mengde varme tilføres enheten Q_inngang = Q₁ fra termotanken ved høy temperatur T₁.
2. Carnots motor C utfører arbeid W takket være denne tilførte varmen.
3. En del av varmen som brukes: avfallet Q_exit, overføres til den termiske tanken som har en lavere temperatur T_to.

Stadier av Carnot-syklusen

Analysen utføres ved hjelp av et PV-diagram (Pressure -Volume), som vist i figur 2 (høyre figur). Hensikten med motoren kan være å holde det termiske reservoaret 2 kjølig og trekke ut varme fra det. I dette tilfellet er det en kjøling maskin. Hvis du derimot vil overføre varme til termisk tank 1, er det en varmepumpe.

P-V-diagrammet viser endringene i motorens trykk - temperatur under to forhold:

- Holde temperaturen konstant (isotermisk prosess).

- Ingen varmeoverføring (varmeisolasjon).

De to isotermiske prosessene må kobles sammen, noe som oppnås ved termisk isolasjon.

Punkt

Du kan starte når som helst i syklusen, der gassen har visse forhold for trykk, volum og temperatur. Gassen gjennomgår en rekke prosesser og kan gå tilbake til startforholdene for å starte en ny syklus, og den endelige interne energien er alltid den samme som den første. Siden energi er bevart:

Arbeid utført av C = Heat input - Heat output

ΔW = Q_inngang - Spørsmål_exit

Området i denne sløyfen eller sløyfen, i turkis på figuren, tilsvarer nøyaktig arbeidet med Carnot-motoren.

I figur 2 er punkt A, B, C og D. Vi markerer punkt A etter den blå pilen..

Første trinn: isoterm ekspansjon

Temperaturen mellom punktene A og B er T₁. Systemet absorberer varme fra det termiske reservoaret 1 og gjennomgår en isoterm ekspansjon. Da øker volumet og trykket avtar.

Imidlertid forblir temperaturen på T₁, siden når gassen utvides, avkjøles den. Derfor forblir den indre energien konstant.

Andre trinn: adiabatisk utvidelse

På punkt B begynner systemet en ny utvidelse der systemet verken får eller mister varme. Dette oppnås ved å plassere den i varmeisolasjon som angitt ovenfor. Derfor er det en adiabatisk utvidelse som fortsetter å peke C etter den røde pilen. Volumet øker og trykket synker til den laveste verdien.

Tredje trinn: isoterm kompresjon

Den begynner ved punkt C og slutter ved D. Isolasjonen fjernes og systemet kommer i kontakt med termisk tank 2, hvis temperatur T_to er mindre. Systemet overfører spillvarme til det termiske reservoaret, trykket begynner å øke og volumet å synke.

Fjerde trinn: adiabatisk kompresjon

Ved punkt D går systemet tilbake til varmeisolasjon, trykket øker og volumet synker til det når de opprinnelige forholdene i punkt A. Deretter gjentas syklusen igjen..

Carnots teorem

Carnots teorem ble først postulert tidlig på 1800-tallet av den franske fysikeren Sadi Carnot. I 1824 utgav Carnot, som var en del av den franske hæren, en bok der han foreslo svaret på følgende spørsmål: under hvilke forhold har en varmemotor maksimal effektivitet? Carnot etablerte deretter følgende:

Ingen varmemotor som går mellom to varmemagasiner er mer effektiv enn Carnot-motoren.

Effektiviteten η til en varmemotor er gitt av kvotienten mellom arbeidet W og den absorberte varmen Q:

ytelse = utført arbeid / varme absorbert

På denne måten er effektiviteten til enhver varmemotor I: η = W / Q. Mens effektiviteten til en Carnot-motor R er η '= W / Q', forutsatt at begge motorene er i stand til å gjøre det samme arbeidet.

Carnots teorem sier at η aldri er større enn η '. Ellers faller det i strid med termodynamikkens andre lov, ifølge hvilken en prosess der resultatet er at varme kommer ut av en kropp med lavere temperatur for å gå til en høyere temperatur uten å motta ekstern hjelp er umulig. Derfor:

η _< η^'

Bevis på Carnots teorem

For å vise at dette er slik, bør du vurdere Carnot-motoren som fungerer som en kjølemaskin som drives av en I. Dette er mulig siden Carnot-motoren fungerer ved reversible prosesser, som spesifisert i begynnelsen..

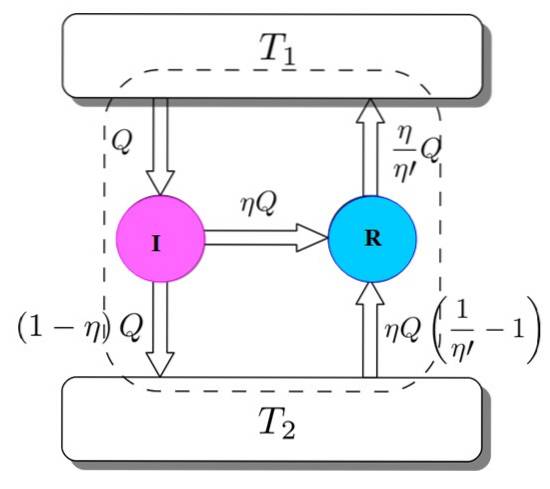
Vi har begge: I og R arbeider med de samme termiske reservoarene, og det antas at η _> η^'. Hvis det underveis oppnås en motsetning med termodynamikkens andre lov, bevises Carnos teorem ved reduksjon til absurditet.

Figur 3 hjelper deg med å følge prosessen. Motoren I tar inn en mengde varme Q, som den deler på denne måten: gjør arbeid på R tilsvarende W = ηQ, og resten er varmen som overføres (1-η) Q til det termiske reservoaret T_to.

Siden energi er bevart, er alt av følgende sant:

OG_inngang = Q = Arbeid W + varme gitt til T_to = ηQ + (1-η) Q = E_exit

Nå tar Carnot kjølemaskin R fra varmebeholderen 2 en mengde varme gitt av:

(η / η ') (1-η') Q =

Energi må også spares i dette tilfellet:

OG_inngang = ηQ + (η / η ') (1-η') Q = (η / η ') Q = Q' = E_exit

Resultatet er overføringen til termotanken T_to av en mengde varme gitt av (η / η ') Q = Q'.

Hvis η er større enn η ', betyr det at mer varme har nådd termisk avleiring av høyere temperatur enn jeg opprinnelig tok. Siden ingen eksterne stoffer, som en annen varmekilde, har deltatt, er den eneste måten å skje på at det kaldeste termiske reservoaret gir opp varmen..

Dette er uenig med termodynamikkens andre lov. Det ble da konkludert med at det ikke er mulig at η^' er mindre enn η, derfor kan motoren I ikke ha mer effektivitet enn Carnot-maskinen R.

Resultat av teorem og begrensninger

Resultatet av Carnots teorem sier at to Carnot-maskiner har samme effektivitet hvis de begge opererer med de samme termiske reservoarene..

Det betyr at uansett stoff, ytelsen er uavhengig og kan ikke løftes ved å endre den..

Konklusjonen fra analysen ovenfor er at Carnot-syklusen er den ideelt oppnåelige toppen av den termodynamiske prosessen. I praksis er det mange faktorer som reduserer effektiviteten, for eksempel det faktum at isolasjonen aldri er perfekt, og i adiabatiske stadier er det faktisk varmeutveksling med utsiden.

I tilfelle en bil blir motorblokken varm. På den annen side oppfører blandingen av bensin og luft seg ikke akkurat som en ideell gass, som er utgangspunktet for Carnot-syklusen. Dette for å nevne noen få faktorer som vil føre til en drastisk reduksjon i ytelsen.

Eksempler

Et stempel inne i en sylinder

Hvis systemet er et stempel innesluttet i en sylinder som i figur 4, stiger stempelet under isotermisk ekspansjon, som man kan se i det første diagrammet ytterst til venstre, og stiger også under adiabatisk ekspansjon.

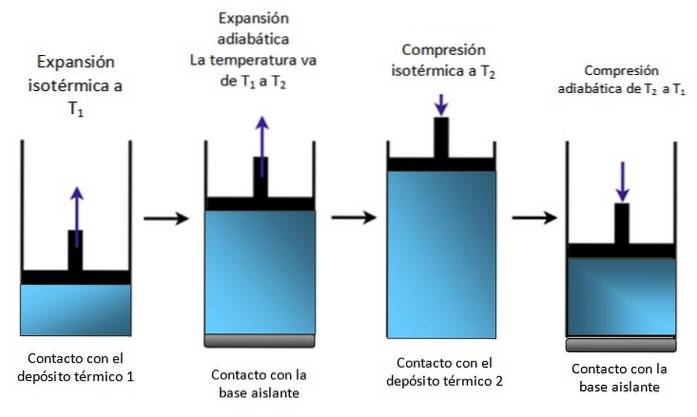
Den komprimeres deretter isotermisk, gir opp varmen og fortsetter å komprimere adiabatisk. Resultatet er en bevegelse der stemplet går opp og ned inne i sylinderen og som kan overføres til andre deler av en bestemt enhet, for eksempel en bilmotor som produserer dreiemoment eller en dampmotor.

Ulike reversible prosesser

I tillegg til utvidelse og kompresjon av en ideell gass inne i en sylinder, er det andre ideelle reversible prosesser som en Carnot-syklus kan konfigureres med, for eksempel:

- Frem og tilbake bevegelser i fravær av friksjon.

- En ideell fjær som komprimerer og dekomprimerer og aldri deformeres.

- Elektriske kretser der det ikke er motstander for å spre energi.

- Magnetiserings- og demagnetiseringssykluser der det ikke er tap.

- Lade og tømme et batteri.

Et atomkraftverk

Selv om det er et veldig komplekst system, er en første tilnærming av det som kreves for å produsere energi i en atomreaktor som følger:

- En termisk kilde, bestående av et radioaktivt råtnende materiale som uran.

- Den kalde varmeavlederen eller reservoaret som ville være atmosfæren.

- "Carnot-motoren" som bruker væske, nesten alltid vann fra springen, som det tilføres varme fra den termiske kilden for å konvertere den til damp.

Når syklusen utføres, oppnås elektrisk energi som nettoarbeid. Når det blir transformert til damp ved høy temperatur, får vannet til å nå en turbin, der energien blir transformert til bevegelse eller kinetisk energi.

Turbinen driver i sin tur en elektrisk generator som forvandler energien til bevegelsen til elektrisk energi. I tillegg til spaltbart materiale som uran, kan selvfølgelig fossile brensler brukes som varmekilde..

Løst øvelser

-Eksempel 1: effektivitet til en varmemotor

Effektiviteten til en varmemotor er definert som kvotienten mellom utgangsarbeidet og inngangsarbeidet, og det er derfor en dimensjonsløs mengde:

Maksimal effektivitet = (Q_inngang - Spørsmål _exit) / Q_inngang

Betegner maksimal effektivitet som e_maks, det er mulig å demonstrere sin avhengighet av temperatur, som er den enkleste variabelen å måle, for eksempel:

og_maks = 1 - (T_to/ T₁)

Hvor T_to er sumptemperaturen og T₁ er temperaturen på varmekilden. Siden sistnevnte er større, viser effektiviteten seg alltid å være mindre enn 1.

Anta at du har en varmemotor som kan fungere på følgende måter: a) Mellom 200 K og 400 K, b) Mellom 600 K og 400 K. Hva er effektiviteten i hvert tilfelle?

Løsning

a) I det første tilfellet er effektiviteten:

og_maks1 = 1 - (200/400) = 0,50

b) For den andre modusen vil effektiviteten være:

og_maks2 = 1- (400/600) = 0,33

Selv om temperaturforskjellen er den samme mellom begge modusene, er effektiviteten ikke. Og enda mer bemerkelsesverdig er at den mest effektive modusen fungerer ved en lavere temperatur..

-Eksempel 2: absorbert varme og frigitt varme

En 22% effektiv varmemotor produserer 1.530 J arbeid. Finn: a) Mengden varme som absorberes fra termisk tank 1, b) Mengden varme som slippes ut til termisk tank 2.

a) I dette tilfellet brukes definisjonen av effektivitet, siden arbeidet som er utført er tilgjengelig, ikke temperaturene til termotankene. En effektivitet på 22% betyr at e _maks = 0,22, derfor:

Maksimal effektivitet = Arbeid / Q_inngang

Mengden absorbert varme er nøyaktig Spørsmål_inngang, så klarering har vi:

Spørsmål_inngang = Arbeid / effektivitet = 1530 J / 0,22 = 6954,5 J

b) Mengden varme som overføres til den kaldeste tanken, blir funnet fra ΔW = Q_inngang - Spørsmål_exit

Spørsmål_exit = Q_inngang - ΔW = 6954,5 -1530 J = 5424,5 J.

En annen måte er fra og_maks = 1 - (T_to/ T₁). Siden temperaturene ikke er kjent, men de er relatert til varme, kan effektiviteten også uttrykkes som:

og_maks = 1 - (Q_{ga etter}/ Q_absorbert)

Referanser

1. Bauer, W. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill. 654-657
2. Kjernekraft. Drift av et atomkraftverk. Gjenopprettet fra: energia-nuclear.net
3. Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning. 618-622.
4. Tippens, P. 2011. Fysikk: Konsepter og applikasjoner. 7. utgave. MacGraw Hill. 414-416.
5. Walker, J. 2008. Fysikk. 4. utgave Addison Wesley. 610-630