
Viktige tall regler, eksempler, løste øvelser
Heter Betydelige tall til antall sifre som finnes i mantissa av et tall. Jo flere tall du har, desto mer presist er antallet kjent. Som en påminnelse er mantissen figuren som følger kraften på 10 når tallet er skrevet i vitenskapelig notasjon..
La oss for eksempel ta tallet 0,00376, som er skrevet som 3,76 x 10 -3. Mantissaen er 3,76 og antallet har totalt 3 betydelige tall. Tallet 0,129 har også 3 signifikante tall, mens 4,5 bare har 2.

Og hva skjer når tallet er et helt tall? Det betyr at den er kjent med så mye presisjon som mulig, med andre ord, den har uendelig presisjon. Når du for eksempel teller mennesker, dyr eller gjenstander som bøker og telefoner, er resultatet et presist heltall.
Hvis vi sier at i en kino er det 110 personer som ser på en film, er dette det nøyaktige antallet, verken mer eller mindre, og det har 3 betydelige tall.
Viktige tall håndteres av noen enkle regler som blir husket med litt øvelse, som vi vil se nedenfor..
Artikkelindeks
- 1 Regler for å bestemme viktige tall for et tall
- 1.1 Regel 1
- 1.2 Regel 3
- 1.3 Regel 4
- 1.4 Regel 5
- 2 Eksempler
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 2.3 Eksempel 3
- 3 Regler for avrunding av tall
- 4 Referanser
Regler for å bestemme viktige tall for et tall
Regel 1
De ledende nullene teller ikke som en signifikant figur, så 0,045 og 4,5 har begge to signifikante tall, siden disse begynner å telles fra venstre og starter fra det første tallet som ikke er null.
Regel 2
Nullene etter (til høyre) det første signifikante tallet teller som en betydelig figur (så lenge det er berettiget av måleinstrumentets presisjon).
Til slutt regnes også nullene i midten som et betydelig siffer..
Regel 3
For tall skrevet med vitenskapelig notasjon er alle figurer i mantissaen betydningsfulle, og eksponenten påvirker ikke presisjonen..
Regel 4
Når du utfører operasjoner med desimaler, for eksempel når du beregner arealer eller andre lignende operasjoner, må resultatet ha samme antall signifikante tall som mengden med færrest antall signifikante figurer som deltok i operasjonen. Denne regelen er gyldig for alle aritmetiske operasjoner.
Regel 5
Tegn på nummeret påvirker ikke antall vesentlige tall.
Vi vil umiddelbart se noen eksempler på dette og alle de andre reglene.
Eksempler
Eksempel 1
Finn hvor mange viktige tall som er i hvert av disse tallene.
a) 876
b) 1000,68
c) 0.00005026
d) 4.8
e) -6,99
Svar
a) 876 har 3 signifikante tall.
b) 1000.68 har 6 signifikante tall, siden nullene i mellom teller som sådan.
c) I stedet har 0.00005026 4 signifikante tall. Merk at 5 nuller til venstre for 5 ikke telles som en betydelig figur, i stedet er 0 som er mellom 5 og 2..
d) 4.8 har 2 signifikante tall.
e) -6.99 har 3 betydelige tall.
Eksempel 2
Det er vanlig å ta målinger med måleinstrumenter, for eksempel målebånd, klokker, termometre, vekter og så videre. Med hvor mange viktige tall skal vi rapportere mengdene vi måler på denne måten??
Svar
Det avhenger av forståelsen av instrumentet som det måles med. La oss ta et eksempel: måle den ytre diameteren på et rør, med en gradert linjal og med en vernier eller tykkelse.
Vernier er et instrument som måler lengder veldig nøyaktig fordi det har en ekstra liten skala, kalt vernier, noe som gir større finhet, så å si, når du måler.
Det er mer presist enn en gradert hersker fordi vi med den kan kjenne til mer betydningsfulle figurer av en viss lengde.
Det er derfor det ikke gir mening å rapportere en omkrets på for eksempel 35,88 cm hvis vi måler det med et målebånd, siden dette instrumentet ikke er nøyaktig nok til å rapportere så mange signifikante sifre..
Takknemligheten A for målebåndet er gitt av:
Eksempel 3
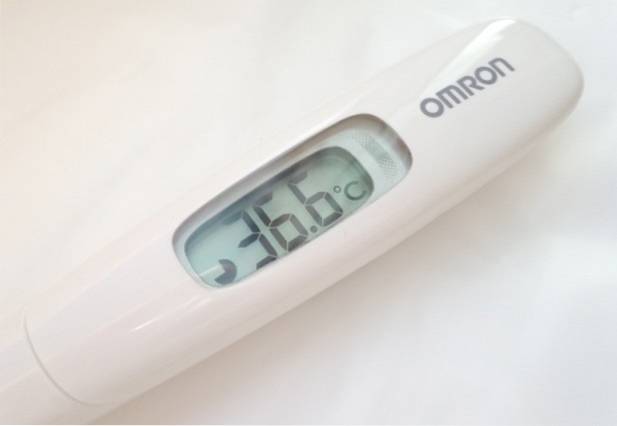
Hvor mange viktige tall har avlesningen med det digitale termometeret?
Svar
Termometeret i figuren gir tresifrede temperaturavlesninger. Imidlertid er målingen, 36,6 ºC, bare de to første sifrene fra venstre til høyre nøyaktige, siden desimalen påvirkes av instrumentets takknemlighet, som vanligvis er angitt på baksiden av instrumentet eller i bruksanvisningen..
Det vanlige for den viste typen digitale instrumenter er en feilvurdering på 0,1 ºC. Dette er nok til å være sikker på at du ikke har feber..

Regler for avrunding av tall
Når du bruker en kalkulator til å utføre beregninger med oppnådde målinger, er det ikke riktig å gi resultatet ved å bruke alle sifrene som vises på skjermen..
Bare de som er nøyaktig kjent blir beholdt, da bare de har ekte mening. Det er da nødvendig å runde resultatene slik at de passer til antall nøyaktig kjente figurer. Disse reglene er:
-Hvis tallet som følger tallet som skal holdes tilbake, er lik eller større enn 5, 1 er lagt til dette sifferet.
Når vi for eksempel avrunder 3.786 til to desimaler, vil vi beholde tallene opp til 8. Siden tallet som følger (6) er større enn 5, blir 8 8 + 1 = 9 og tallet forblir som 3,79.
-Når tallet som følger tallet som skal holdes, er mindre enn 5, sifferet forblir det samme.
Hvis vi ønsker å runde 1.27924 slik at den bare har 3 desimaler, oppnås dette ved å nå 9, som følges av 2. Siden 2 er mindre enn 5, forsvinner disse desimalene og det avrundede tallet forblir 1,279.
Treningen løst
Et spisebord har form og dimensjoner som er angitt i den medfølgende figuren. Du blir bedt om å beregne området ved hjelp av operasjonsreglene med betydelige tall.
Løsning
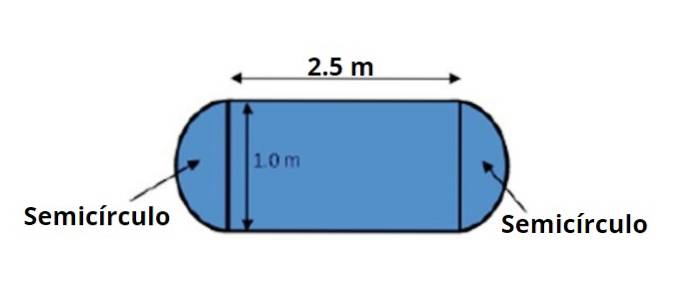
Bordområdet kan deles inn i et sentralt rektangulært område og to halvsirkler, en på hver side, som til sammen utgjør en hel sirkel.
Vi vil kalle A1 til området av rektangelet, gitt av:
TIL1 = sokkel × høyde = 2,5 m x 1,0 m = 2,5 mto
For sin del er arealet av sirkelen, som er lik det for en halvsirkel multiplisert med 2:
TILto = π × radiusto
Diameteren til en av halvcirklene er 1,0 m, derfor er radien 0,50 m. Diameteren kan også brukes direkte til å beregne arealet, i dette tilfellet:
TILto = (π × diameterto) / 4
I alle fall:
TILto = [π x (1,0 m)to] / 4 = 0,785398163 mto
Alle sifrene fra kalkulatoren ble brukt. Nå legger vi til A1 alleredeto for det totale arealet A av tabellen:
A = (2,5 + 0,785398163) mto = 3.285398163 mto
Ettersom dimensjonene på tabellen er kjent for to signifikante figurer, er det ikke fornuftig å uttrykke resultatet med alle desimalene gitt av kalkulatoren, som aldri gir antall signifikante figurer av et resultat.
Det du må gjøre er å runde området slik at det har samme antall signifikante figurer som dimensjonene på tabellen, det vil si 2. Derfor blir det endelige resultatet rapportert som følger:
A = 3,3 mto
Referanser
- Bauer, W. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).
- Fisicalab. Betydelige tall og avrunding. Gjenopprettet fra: fisicalab.com.
- Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. Sjette. Ed prentice hall.
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 1.


Ingen har kommentert denne artikkelen ennå.