
Vekselstrømskretstyper, applikasjoner, eksempler
De vekselstrømskretser eller vekselstrømskretser består av kombinasjoner av resistive, induktive og kapasitive elementer, kombinert med en vekselstrømskilde, som vanligvis er sinusformet.
Ved å påføre spenningen etableres en variabel strøm i kort tid, kalt en forbigående strøm, som gir vei til den sinusformede stående strømmen.
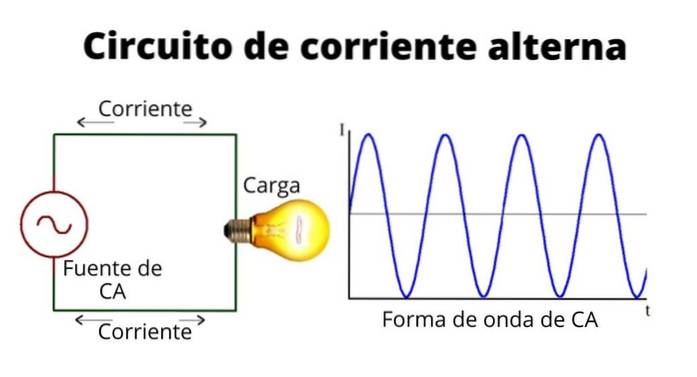
Sinusformet strøm har verdier som veksler mellom positiv og negativ, og endres med jevne mellomrom bestemt av en tidligere etablert frekvens. Strømformen uttrykkes som:
I (t) = Im synd (ωt - φ)
Hvor jegm er maksimal strøm eller strømamplitude, ω er frekvensen, t er tiden og φ faseforskjellen. Vanlige enheter for strøm er ampere (A) og dens submultipler, slik som milliampere og mikroampere..
For sin del måles tiden i sekunder, for frekvensen er det hertz eller Hertz, forkortet Hz, mens faseforskjellen er en vinkel som vanligvis måles i radianer, selv om den også noen ganger er gitt i grader. Verken disse eller radianene regnes som enheter.

Vekselspenningen symboliseres ofte av bølgen inne i sirkelen, for å skille den fra likespenningen, symbolisert av de to ulike og parallelle linjene..
Artikkelindeks
- 1 Typer vekselstrømskretser
- 1.1 Krets med resistivt element
- 1.2 Krets med induktivt element
- 1.3 Krets med kapasitivt element
- 2 Søknader
- 2.1 Faseskiftende kretser
- 2.2 Brokretser
- 3 Eksempler på vekselstrømkretser
- 3.1 Eksempel 1: Serie RLC-krets
- 3.2 Eksempel 2: RLC-krets parallelt
- 4 Øvelse løst
- 4.1 Løsning a
- 4.2 Løsning b
- 4.3 Løsning c
- 5 Temaer av interesse
- 6 Referanser
Typer vekselstrømskretser
Det er mange typer vekselstrømkretser, og starter med de enkleste kretsene vist i følgende figur. Fra venstre til høyre har du:
-Krets med motstand R
-Krets med spole L
-Krets med kondensator C.

Krets med resistivt element
I kretsen med en motstand R koblet til en alternerende spenningskilde, er spenningen over motstanden V.R = Vm sen ωt. I henhold til Ohms lov, som også er gyldig for rent resistive vekselstrømkretser:
VR = JegR∙ R
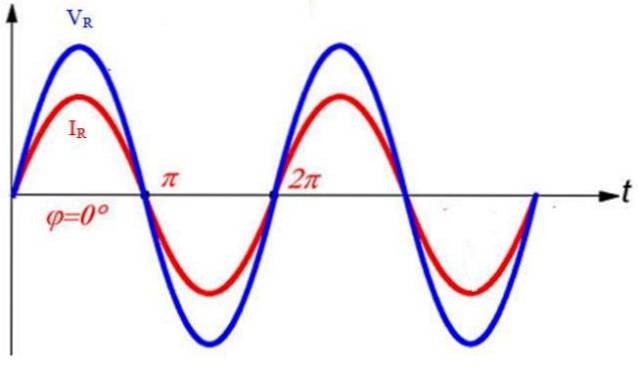
Derfor er den maksimale strømmen jegm = Vm / R.
Både strøm og spenning er i fase, noe som betyr at de når sine maksimale verdier, så vel som 0, samtidig.

Induktivt elementkrets
I spole L er spenningen V.L = Vm sin ωt og er relatert til strømmen i induktoren ved ligningen:
Integrering:

Ved egenskaper av trigonometriske forhold, IL er skrevet i form av synd ast som:
JegL = Jegm sin (ωt - ½ π)
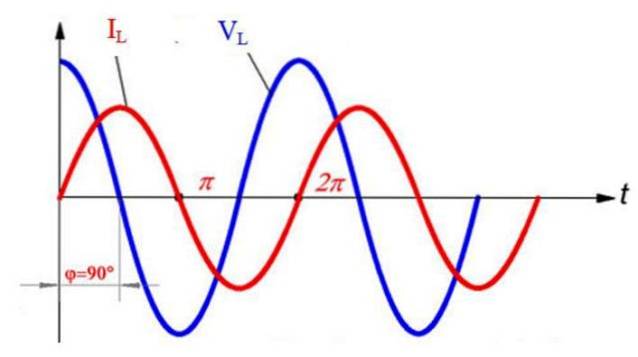
Deretter er spenningen og strømmen ute av fase, sistnevnte halter ½ π = 90º i forhold til spenningen (strømmen starter tidligere, med t = 0 s startpunktet). Dette ses i den følgende figuren som sammenligner sinus av I.L og det til VL:

Induktiv reaktans
Induktiv reaktans er definert som XL = ωL, øker med frekvens og har dimensjoner av motstand, derfor analogt med Ohms lov:
VL = JegL ∙ XL
Krets med kapasitivt element
For en kondensator C koblet til en vekselstrømskilde, er det sant at:
Q = C ∙ VC = C ∙ Vm sen ωt
Strømmen i kondensatoren blir funnet ved å forskyve ladningen med hensyn til tid:
JegC= ωC ∙ Vm cos ωt
Men cos ωt = sin (ωt + ½ π), så:
JegC = ωCVm sin (ωt + ½ π)
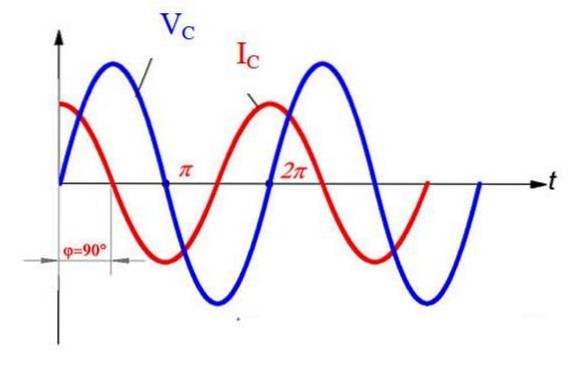
I dette tilfellet fører strømmen spenningen med ½ π, som det fremgår av grafen.

Kapasitiv reaktans
Kapasitiv reaktans kan skrives XC = 1 / ωC, den avtar med frekvens og har også motstandsenheter, det vil si ohm. På denne måten ser Ohms lov slik ut:
VC = XC.JegC
applikasjoner
Michael Faraday (1791-1867) var den første som oppnådde en strøm som med jevne mellomrom endret betydningen, gjennom hans induksjonseksperimenter, men i løpet av de første dagene ble bare likestrøm brukt..
På slutten av 1800-tallet inntraff den velkjente strømmen, mellom Thomas A. Edison, forsvarer for bruk av likestrøm og George Westinghouse, tilhenger av vekselstrøm. Til slutt var dette den som vant på grunn av økonomi, effektivitet og enkel overføring med lavere tap..
Av denne grunn er strømmen som når hjem og næringer hittil vekselstrøm, selv om bruken av likestrøm aldri har forsvunnet helt..
Vekselstrøm brukes til nesten alt, og i mange applikasjoner er konstant retningsendring av vekselstrøm ikke relevant, for eksempel lyspærer, strykejernet eller komfyren for matlaging, siden oppvarmingen av det resistive elementet ikke avhenger av retningen på lastene.
I stedet er det faktum at strømmen endrer retning med en viss frekvens grunnlaget for elektriske motorer og forskjellige mer spesifikke applikasjoner, for eksempel følgende:
Faseskiftende kretser
Kretser bestående av en vekslende kilde koblet til en motstand og en kondensator i serie er kjent som kretser i RC-serien og brukes til å eliminere uønskede faseforskyvninger i en annen krets, eller for å legge til en spesiell effekt på den..
De fungerer også som spenningsdelere og for å stille inn radiostasjoner (se eksempel 1 i neste avsnitt).
Brokretser
Bro-type kretser matet med vekselstrøm kan brukes til å måle kapasitans eller induktans, på samme måte som Wheatstone-broen, en kjent likestrømskrets som er i stand til å måle verdien av en ukjent motstand..
Eksempler på vekselstrømkretser
I de foregående avsnittene ble de enkleste vekselstrømkretsene beskrevet, selv om de grunnleggende elementene som er beskrevet ovenfor, så vel som andre litt mer komplekse som dioder, forsterkere og transistorer, kan kombineres for å oppnå forskjellige effekter. ..
Eksempel 1: Serie RLC-krets
En av de vanligste kretsene i AC er den som inkluderer en motstand R, en spole eller induktor L og en kondensator eller kondensator C plassert i serie med en vekselstrømskilde.
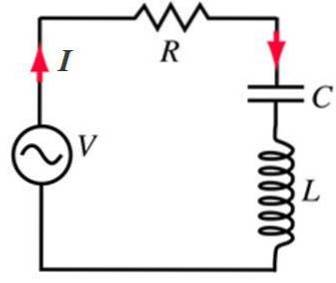
Serien RLC-kretser reagerer på en bestemt måte på frekvensen til den vekslende kilden de mates fra. Derfor er en av de mest interessante applikasjonene som radio-tunerkretser..
Et radiosignal med frekvens ω genererer en strøm med samme frekvens i en krets spesielt designet for å tjene som mottaker, og amplituden til denne strømmen er maksimal hvis mottakeren er innstilt på den frekvensen, gjennom en effekt som kalles resonans.
Mottakerkretsen fungerer som en tuner fordi den er designet slik at signaler om uønskede frekvenser genererer svært små strømmer, som ikke blir oppdaget av radiohøyttalerne og derfor ikke høres. I stedet for, ved resonansfrekvensen, når amplituden til strømmen et maksimum, og deretter høres signalet tydelig..
Resonansfrekvensen oppstår når kretsens induktive og kapasitive reaktanser utjevner:
XL = XC
1 / ωC = ωL
ωto = 1 / LC
Radiostasjonen med frekvenssignalet said sies å være "innstilt", og verdiene til L og C velges for den aktuelle frekvensen..
Eksempel 2: RLC-krets parallelt
Parallelle RLC-kretser har også visse responser i henhold til frekvensen til kilden, som avhenger av reaktansen til hvert av elementene, definert som forholdet mellom spenning og strøm..
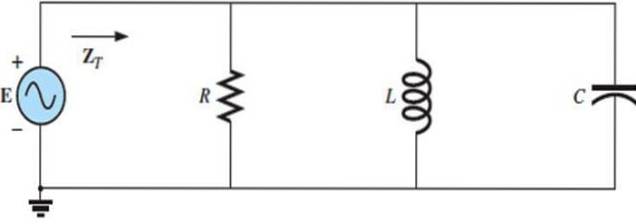
Treningen løst
I serien LRC-kretsen i eksempel 1 i forrige avsnitt er motstanden 200 ohm, induktansen er 0,4 H, og kondensatoren er 6 μF. Strømforsyningen er på sin side en alternerende spenning med amplitude lik 30 V, med en frekvens på 250 rad / s. Det blir bedt om å finne:
a) Reaktansene til hvert element
b) Verdien av modulen for kretsens impedans.
c) Strømens amplitude
Løsning til
De respektive reaktansene beregnes med formlene:
XC = 1 / ωC = 1 / (250 rad / s x 6 x 10-6 F) = 666,67 ohm
XL = ωL = 250 rad / s x 0,4 H = 100 ohm
Og motstandens reaktans er lik verdien i ohm:
XR = R = 200 ohm
Løsning b
Impedans Z er definert som forholdet mellom spenning og strøm i kretsen, enten i serie eller parallelt:
Z = Vm / JEGm
Impedansen måles i ohm, det samme som en motstand eller en reaktans, men det refererer til motstanden mot strømmen til induktansene og kondensatorene, med tanke på at i tillegg til dens spesielle effekter, for eksempel å forsinke eller fremme spenningen, den har også en viss indre motstand.
Det kan vises at impedansmodulen for serien RLC-krets er gitt av:
Når vi vurderer verdiene gitt i uttalelsen, får vi:

Løsning c
Fra:
Z = Vm / JEGm
Det må;
Jegm = Vm / Z = 30V / 601 ohm = 0,05 A..
Temaer av interesse
Forskjeller mellom vekselstrøm og likestrøm
Referanser
- Alexander, C. 2006. Grunnleggende om elektriske kretser. 3.. Utgave. Mc Graw Hill.
- Boylestad, R. 2011. Introduksjon til kretsanalyse.2da. Utgave. Pearson.
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volum 6. Elektromagnetisme. Redigert av Douglas Figueroa (USB).
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 1. Pearson.
- Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.



Ingen har kommentert denne artikkelen ennå.