
Endelige settegenskaper, eksempler, løste øvelser
Det forstås av endelig sett ethvert sett med et begrenset eller tellbart antall elementer. Eksempler på endelige sett er kulene som finnes i en pose, settet med hus i et nabolag eller settet P dannet av de første tjue (20) naturlige tallene:
P = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
Sett med stjerner i universet er helt sikkert enormt, men det er ikke kjent med sikkerhet om det er endelig eller uendelig. Imidlertid er settet med planeter i solsystemet endelig.
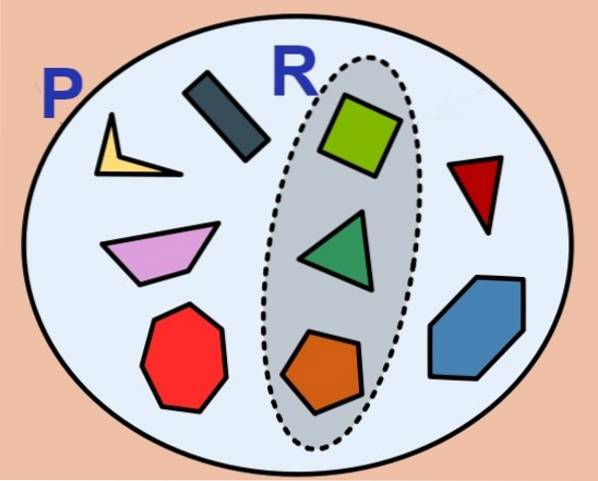
Antall elementer i et endelig sett kalles kardinaliteten og for settet P er betegnet slik: Kort (P) eller #P. Det tomme settet har null kardinalitet og betraktes som et endelig sett.
Artikkelindeks
- 1 eiendommer
- 2 Eksempler
- 2.1 Flere eksempler
- 3 løste øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 3.3 Øvelse 3
- 3.4 Øvelse 4
- 4 Referanser
Eiendommer
Blant egenskapene til endelige sett er følgende:
1- Foreningen av endelige sett gir opphav til et nytt endelig sett.
2- Hvis to endelige sett krysser hverandre, resulterer det i et nytt endelig sett.
3- En delmengde av et endelig sett er endelig, og dets kardinalitet er mindre enn eller lik det originale settet.
4- Det tomme settet er et endelig sett.
Eksempler
Det er mange eksempler på endelige sett. Noen eksempler inkluderer følgende:
Sett M av månedene i året, som i utvidet form kan skrives slik:
M = Januar, februar, mars, april, mai, juni, juli, august, september, oktober, november, desember, kardinaliteten til M er 12.
Sett S av ukedagene: S = Mandag, tirsdag, onsdag, torsdag, fredag, lørdag, søndag. Kardinaliteten til S er 7.
Sett Ñ av bokstavene i det spanske alfabetet er et endelig sett, dette settet som forlengelse er skrevet slik:
Ñ = a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z og dens kardinalitet er 27.
Sett V av vokalene på spansk er en delmengde av settet Ñ:
V ⊂ Ñ derfor er det et endelig sett.
Det endelige settet V i omfattende form er det skrevet slik: V = a, e, i, o, u og dens kardinalitet er 5.
Sett kan uttrykkes ved forståelse. Sett F består av bokstavene i ordet "endelig" er et eksempel:
F = x / x er en bokstav i ordet "endelig"
Nevnte sett uttrykt på en omfattende måte vil være:
F = f, i, n, t, o hvis kardinalitet er 5 og derfor er et endelig sett.
Flere eksempler
Regnbuens farger er et annet eksempel på et endelig sett, settet C av disse fargene er:
C = rød, oransje, gul, grønn, cyan, blå, fiolett og dens kardinalitet er 7.
Fasesettet F de la Luna er et annet eksempel på et endelig sett:
F = New moon, first quarter, full moon, last quarter dette settet har kardinalitet 4.
Et annet endelig sett er det som dannes av solsystemets planeter:
P = Kvikksølv, Venus, Jorden, Mars, Jupiter, Saturn, Uranus, Neptun, Pluto av kardinaliteten 9.
Løste øvelser
Øvelse 1
Følgende sett A = x∊ R / x ^ 3 = 27 er gitt. Uttrykk det med ord og skriv det i forlengelse, angi kardinaliteten og si om det er endelig eller ikke.
Løsning: Sett A er settet med reelle tall x slik at x kubikk av som et resultat 27.
Ligningen x ^ 3 = 27 har tre løsninger: de er x1 = 3, x2 = (-3/2 + 3√3 / 2 i) og x3 = (-3/2 - 3√3 / 2 i). Av de tre løsningene er bare x1 reell, mens de to andre er komplekse tall.
Siden definisjonen av mengden A sier at x tilhører de reelle tallene, er ikke løsningene i de komplekse tallene en del av settet A.
Settet A uttrykt mye er:
A = 3, som er et endelig sett med kardinalitet 1.
Øvelse 2
Skriv i symbolsk form (etter forståelse) og i omfattende form mengden B av reelle tall som er større enn 0 (null) og mindre enn eller lik 0 (null). Angi kardinaliteten og om den er endelig eller ikke.
Løsning: B = x∊ R / 0 < x <= 0
Settet B er tom fordi et reelt tall x ikke kan være større og mindre enn null samtidig, akkurat som det ikke kan være 0 og også mindre enn 0.
B = og kardinaliteten er 0. Det tomme settet er et endelig sett.
Øvelse 3
Settet S for løsningene til en bestemt ligning er gitt. Settet S ved forståelse er skrevet slik:
S = x∊ R / (x-3) (x ^ 2 - 9x + 20) = 0
Skriv settet i omfattende form, angi kardinaliteten og angi om det er et endelig sett.
Løsning: For det første, når man analyserer uttrykket som beskriver settet S, oppnås det at det er et sett med reelle x-verdier som er løsninger av ligningen:
(x-3) (x ^ 2 - 9x + 20) = 0 (*)
En løsning av denne ligningen er x = 3, som er et reelt tall og tilhører derfor S. Men det er flere løsninger som kan oppnås ved å se etter løsningene i den kvadratiske ligningen:
(x ^ 2 - 9x + 20) = 0
Ovennevnte uttrykk kan tenkes som følger:
(x - 4) (x - 5) = 0
Som fører oss til to flere løsninger av den opprinnelige ligningen (*) som er x = 4 og x = 5. Kort sagt har ligningen (*) som løsning 3, 4 og 5.
Settet S uttrykt i omfattende form ser slik ut:
S = 3, 4, 5, som har kardinalitet 3 og derfor er et endelig sett.
Øvelse 4
Det er to sett A = 1, 5, 7, 9, 11 og B = x ∊ N / x er jevn ^ x < 10 .
Skriv eksplisitt sett B og finn foreningen med mengden A. Finn også skjæringspunktet til disse to settene og avslutt.
Løsning: mengde B består av naturlige tall slik at de er jevne og også er mindre enn verdien 10, derfor er det i sett B i omfattende form skrevet som følger:
B = 2, 4, 6, 8
Foreningen av sett A med sett B er:
A U B = 1, 2, 4, 5, 6, 7, 8, 9, 11
og skjæringspunktet til sett A med sett B er skrevet slik:
A ⋂ B = = Ø er det tomme settet.
Det skal bemerkes at foreningen og avlyttingen av disse to endelige settene fører til nye sett, som igjen også er endelige.
Referanser
- Fuentes, A. (2016). GRUNNLEGGENDE MATH. En introduksjon til kalkulus. Lulu.com.
- Garo, M. (2014). Matematikk: kvadratiske ligninger: Hvordan løse en kvadratisk ligning. Marilù Garo.
- Haeussler, E. F., & Paul, R. S. (2003). Matematikk for ledelse og økonomi. Pearson Education.
- Jiménez, J., Rodríguez, M., Estrada, R. (2005). Matematikk 1 SEP. Terskel.
- Preciado, C. T. (2005). Matematikkurs 3.. Redaksjonell Progreso.
- Matematikk 10 (2018). "Eksempler på endelige sett". Gjenopprettet fra: matematicas10.net
- Rock, N. M. (2006). Algebra I Is Easy! Så lett. Team Rock Press.
- Sullivan, J. (2006). Algebra og trigonometri. Pearson Education.
- Wikipedia. Endelig sett. Gjenopprettet fra: es.wikipedia.com



Ingen har kommentert denne artikkelen ennå.