
Sylindriske koordinatsystem, endring og øvelser
De sylindriske koordinater de tjener til å lokalisere punkter i tredimensjonalt rom og består av en radiell koordinat ρ, en azimutkoordinat φ og en høydekoordinat z.
Et poeng P plassert i rommet projiseres loddrett på flyet XY som gir opphav til poenget P ' i det flyet. Avstanden fra opprinnelsen til punktet P ' definerer koordinaten ρ, mens vinkelen dannes av aksen X med strålen OP ' definerer koordinaten φ. Til slutt koordinaten z er den ortogonale projeksjonen av punktet P på aksen Z. (se figur 1).
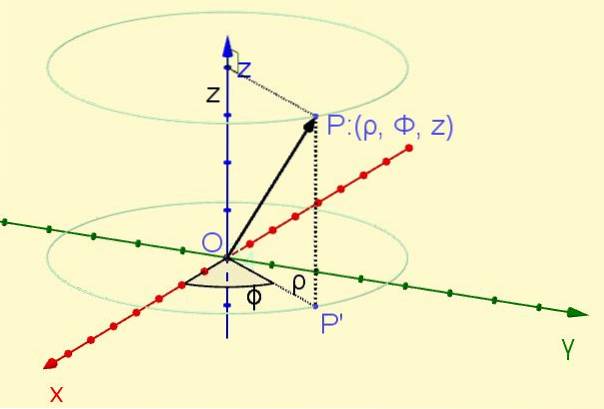
Den radiale koordinaten ρ er alltid positiv, den azimutale koordinaten φ varierer fra null radianer til to pi radianer, mens z-koordinaten kan ta en hvilken som helst reell verdi:
0 ≤ ρ < ∞
0 ≤ φ < 2π
- ∞ < z < + ∞
Artikkelindeks
- 1 Koordinatendring
- 1.1 Vektorbase i sylindriske koordinater
- 2 Eksempler
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 3 Løst øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 3.3 Øvelse 3
- 3.4 Øvelse 4
- 4 Referanser
Koordinatendring
Det er relativt enkelt å få tak i de kartesiske koordinatene (x, y, z) for et punkt P fra de sylindriske koordinatene (ρ, φ, z):
x = ρ cos (φ)
y = ρ sin (φ)
z = z
Men det er også mulig å oppnå polarkoordinatene (ρ, φ, z) ut fra kunnskapen om de kartesiske koordinatene (x, y, z) for et punkt P:
ρ = √ (xto + Yto)
φ = arctan (y / x)
z = z
Vector base i sylindriske koordinater
Basen til sylindriske enhetsvektorer er definert Uρ, Uφ, Uz.
Vektoren Uρ er tangent til linjen φ = ctte og z = ctte (peker radielt utover), vektoren Uφ er tangent til linjen ρ = ctte og z = ctte og til slutt Uz har samme retning av Z-aksen.
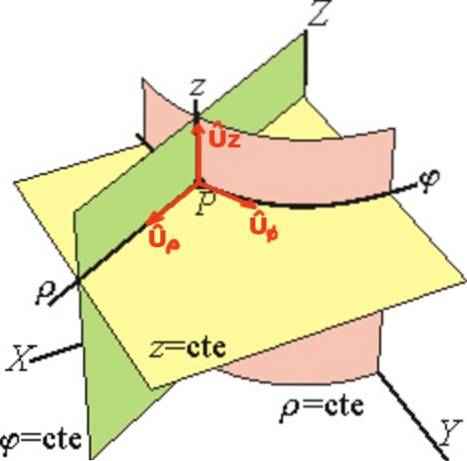
I den sylindriske enhetsbasen, posisjonsvektoren r av et punkt P er skrevet vektorisk slik:
r = ρ Uρ + 0 Uφ + z Uz
På den annen side, en uendelig liten forskyvning dr fra punkt P uttrykkes det som følger:
dr = dρ Uρ + ρ dφ Uφ + dz Uz
Tilsvarende er et uendelig lite element av volum dV i sylindriske koordinater:
dV = ρ dρ dφ dz
Eksempler
Det er utallige eksempler på bruk og anvendelse av sylindriske koordinater. I kartografi, for eksempel, sylindrisk projeksjon, basert nettopp på disse koordinatene. Det er flere eksempler:
Eksempel 1
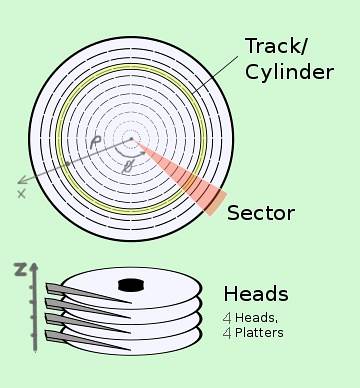
Sylindriske koordinater har anvendelser innen teknologi. Som et eksempel har vi CHS-systemet (Cylinder-Head-Sector) for å finne data på en harddisk, som faktisk består av flere disker:
- Sylinderen eller sporet tilsvarer koordinaten ρ.
- Sektoren tilsvarer posisjonen φ på disken som roterer høyt vinkelhastighet.
- Hodet tilsvarer z-posisjonen til lesehodet på den tilsvarende disken.
Hver informasjonsbyte har en presis adresse i sylindriske koordinater (C, S, H).
Eksempel 2
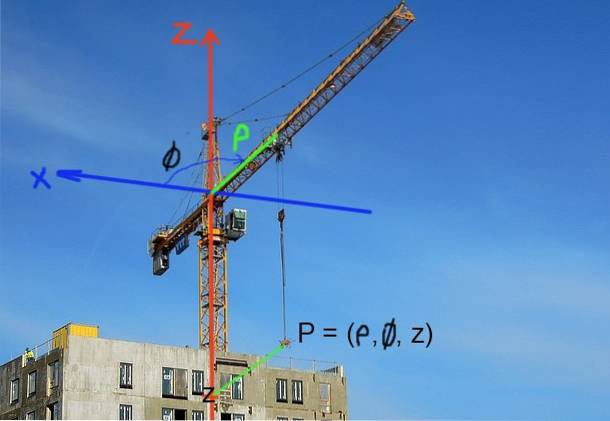
Byggekraner fikser lastens posisjon i sylindriske koordinater. Den horisontale posisjonen er definert av avstanden til aksen eller pilen til kranen ρ og av dens vinkelposisjon φ i forhold til noen referanseakse. Lastens vertikale posisjon bestemmes av z-koordinaten til høyden.
Løst øvelser
Øvelse 1
Det er punkter P1 med sylindriske koordinater (3, 120º, -4) og punkt P2 med sylindriske koordinater (2, 90º, 5). Finn Euklidisk avstand mellom disse to punktene.
Løsning: Først fortsetter vi med å finne de kartesiske koordinatene for hvert punkt i henhold til formelen gitt ovenfor.
P1 = (3 * cos 120º, 3 * sin 120º, -4) = (-1,5, 2,60, -4)
P2 = (2 * cos 90º, 2 * sin 90º, 5) = (0, 2, 5)
Den euklidiske avstanden mellom P1 og P2 er:
d (P1, P2) = √ ((0 - (-1,5))to+(2 - 2,60)to+(5 - (- 4))to ) = ...
… √ (2,25 + 0,36 + 81) = 9,14
Øvelse 2
Punkt P har kartesiske koordinater (-3, 4, 2). Finn de tilsvarende sylindriske koordinatene.
Løsning: Vi fortsetter med å finne de sylindriske koordinatene ved hjelp av forholdene gitt ovenfor:
ρ = √ (xto + Yto) = √ ((- 3)to + 4to) = √ (9 + 16) = √ (25) = 5
φ = arctan (y / x) = arctan (4 / (- 3)) = -53,13º + 180º = 126,87º
z = 2
Det skal huskes at den arktangente funksjonen er multivurdert med 180 ° periodicitet. Også vinkelen φ må tilhøre den andre kvadranten, siden x- og y-koordinatene til punkt P er i den kvadranten. Dette er grunnen til at 180º er lagt til resultatet φ.
Øvelse 3
Uttrykke i sylindriske koordinater og i kartesiske koordinater overflaten til en sylinder med radius 2 og hvis akse sammenfaller med Z-aksen.
Løsning: Det er forstått at sylinderen har en uendelig forlengelse i z-retning, så ligningen av overflaten i sylindriske koordinater er:
ρ = 2
For å oppnå den kartesiske ligningen av den sylindriske overflaten, tas kvadratet til begge elementene i den forrige ligningen:
ρto = 4
Vi multipliserer med 1 begge medlemmene av den forrige likheten og bruker grunnleggende trigonometrisk identitet (sento(φ) + costo(φ) = 1):
1 * ρto = 1 * 4
(sento(φ) + costo(φ)) * ρto = 1 * 4
Parentesen er utviklet for å oppnå:
(ρ sin (φ))to + (ρ cos (φ))to = 4
Vi husker at de første parentesene (ρ sin (φ)) er y-koordinaten til et punkt i polare koordinater, mens parentesene (ρ cos (φ)) representerer x-koordinaten, slik at vi har ligningen til sylinderen i kartesiske koordinater:
Yto + xto = 2to
Den forrige ligningen skal ikke forveksles med sirkelen i XY-planet, siden det i dette tilfellet vil se slik ut: yto + xto = 2to ; z = 0.
Øvelse 4
En sylinder med radius R = 1 m og høyde H = 1m har massen fordelt radialt i henhold til følgende ligning D (ρ) = C (1 - ρ / R) hvor C er en konstant med verdien C = 1 kg / m3. Finn den totale massen til sylinderen i kilo.
Løsning: Det første er å innse at funksjonen D (ρ) representerer den volumetriske massetettheten, og at massetettheten fordeles i sylindriske skall med avtagende tetthet fra sentrum til periferien. Et uendelig lite volumelement i henhold til problemets symmetri er:
dV = ρ dρ 2π H
Derfor vil den uendelige minimale massen til et sylindrisk skall være:
dM = D (ρ) dV
Derfor vil den totale massen til sylinderen uttrykkes av følgende bestemt integral:
M = ∫ellerR D (ρ) dV = ∫ellerR C (1 - ρ / R) ρ dρ 2π H = 2π H C ∫ellerR (1 - ρ / R) ρ dρ
Løsningen på den angitte integralen er ikke vanskelig å oppnå, og resultatet er:
∫ellerR (1 - ρ / R) ρ dρ = (⅙) Rto
Å innlemme dette resultatet i uttrykket av sylindermassen, får vi:
M = 2π H C (⅙) Rto = ⅓ π H C Rto =
⅓ π 1m * 1kg / m3* 1mto = π / 3 kg ≈ 1,05 kg
Referanser
- Arfken G og Weber H. (2012). Matematiske metoder for fysikere. En omfattende guide. 7. utgave. Akademisk presse. ISBN 978-0-12-384654-9
- Beregning cc. Løste problemer med sylindriske og sfæriske koordinater. Gjenopprettet fra: calculo.cc
- Weisstein, Eric W. "Sylindriske koordinater." Fra MathWorld-A Wolfram Web. Gjenopprettet fra: mathworld.wolfram.com
- wikipedia. Sylindrisk koordinatsystem. Gjenopprettet fra: en.wikipedia.com
- wikipedia. Vektorfelt i sylindriske og sfæriske koordinater. Gjenopprettet fra: en.wikipedia.com

Ingen har kommentert denne artikkelen ennå.