
Suksessive derivater (med løste øvelser)
De påfølgende derivater er derivatene av en funksjon etter det andre derivatet. Prosessen for å beregne de suksessive derivatene er som følger: vi har en funksjon f, som vi kan utlede og dermed oppnå den avledede funksjonen f '. Vi kan utlede dette derivatet av f igjen og oppnå (f ')'.
Denne nye funksjonen kalles det andre derivatet; alle derivater beregnet fra det andre er suksessive; Disse, også kalt høyere orden, har gode applikasjoner, for eksempel å gi informasjon om grafen til en funksjon, testen av det andre derivatet for relative ekstremer og bestemmelse av uendelige serier.

Artikkelindeks
- 1 Definisjon
- 1.1 Eksempel 1
- 1.2 Eksempel 2
- 2 Hastighet og akselerasjon
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 3 applikasjoner
- 3.1 Implisitt avledning
- 3.2 Eksempel
- 3.3 Relative ekstremer
- 3.4 Eksempel
- 3.5 Taylor-serien
- 3.6 Eksempel
- 4 Referanser
Definisjon
Ved å bruke Leibnizs notasjon har vi at derivatet av en funksjon "y" med hensyn til "x" er dy / dx. For å uttrykke det andre derivatet av "y" ved hjelp av Leibnizs notasjon, skriver vi som følger:

Generelt kan vi uttrykke suksessive derivater som følger med Leibnizs notasjon, der n representerer rekkefølgen på derivatet.

Andre notasjoner som brukes er følgende:
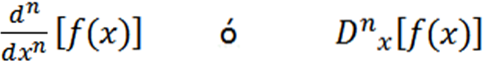
Noen eksempler der vi kan se de forskjellige notasjonene er:
Eksempel 1
Få alle derivater av funksjonen f definert av:
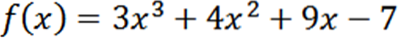
Ved å bruke de vanlige derivasjonsteknikkene har vi at derivatet av f er:

Ved å gjenta prosessen kan vi oppnå det andre derivatet, det tredje derivatet og så videre.
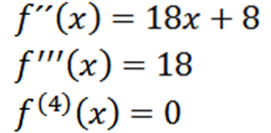
Merk at det fjerde derivatet er null og derivatet til null er null, så vi har:

Eksempel 2
Beregn det fjerde derivatet av følgende funksjon:
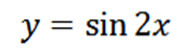
Ved å utlede den gitte funksjonen har vi som et resultat:
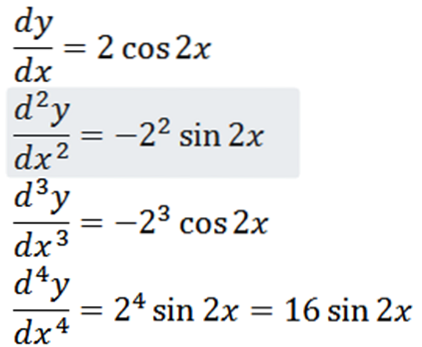
Hastighet og akselerasjon
En av motivasjonene som førte til oppdagelsen av derivatet var søket etter definisjonen av øyeblikkelig hastighet. Den formelle definisjonen er som følger:
La y = f (t) være en funksjon hvis graf beskriver banen til en partikkel på et øyeblikk t, deretter blir hastigheten på et øyeblikk gitt av:

Når en partikkels hastighet er oppnådd, kan vi beregne øyeblikkelig akselerasjon, som er definert som følger:
Den øyeblikkelige akselerasjonen til en partikkel hvis bane er gitt av y = f (t) er:

Eksempel 1
En partikkel beveger seg langs en linje i henhold til posisjonsfunksjonen:

Der "y" måles i meter og "t" i sekunder.
- På hvilket øyeblikk er hastigheten 0?
- På hvilket øyeblikk er akselerasjonen 0?
Når man utleder posisjonen "y", har vi at hastigheten og akselerasjonen er gitt henholdsvis av:

For å svare på det første spørsmålet er det nok å bestemme når funksjonen v blir null; dette er:
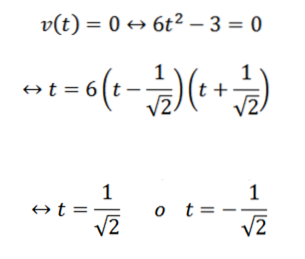
Vi fortsetter med følgende spørsmål på en analog måte:

Eksempel 2
En partikkel beveger seg langs en linje i henhold til følgende bevegelsesligning:

Bestem "t, y" og "v" når a = 0.
Å vite at hastighet og akselerasjon er gitt av

Vi fortsetter å utlede og oppnå:

Å lage a = 0, har vi:
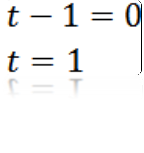
Fra hvor vi kan utlede at verdien av t slik at a er lik null er t = 1.
Deretter vurderer vi posisjonsfunksjonen og hastighetsfunksjonen ved t = 1, vi har:

applikasjoner
Eksplisitt avledning
Suksessive derivater kan også oppnås ved implisitt derivasjon.
Eksempel
Gitt følgende ellips, finn “y”:

Deriverende implisitt med hensyn til x, har vi:
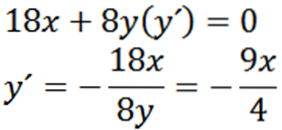
Deretter gir vi oss implisitt omledelse med hensyn til x:

Til slutt har vi:
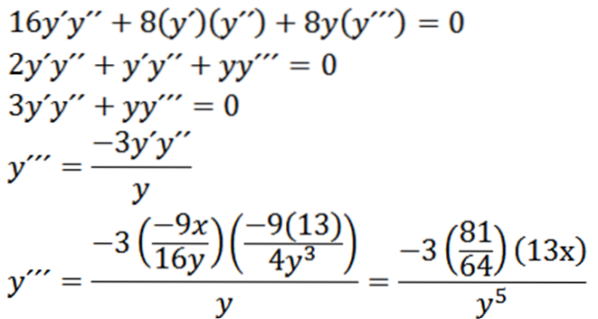
Relative ekstremer
En annen bruk som vi kan gi derivatene av andre orden er i beregningen av relative ekstremer av en funksjon.
Kriteriet for det første derivatet for lokale ekstremer forteller oss at hvis vi har en kontinuerlig funksjon f i et intervall (a, b) og det eksisterer et c som tilhører intervallet slik at f 'forsvinner i c (det vil si at c er et kritisk punkt), kan en av tre tilfeller oppstå:
- Hvis f '(x)> 0 for alle x som tilhører (a, c) og f' (x)<0 para x perteneciente a (c,b), entonces f(c) es un máximo local.
- Hvis f '(x) < 0 para cualquier x perteneciente a (a,c) y f'(x)>0 for x som tilhører (c, b), så er f (c) et lokalt minimum.
- Hvis f '(x) har samme logg på (a, c) og i (c, b), innebærer det at f (c) ikke er en lokal ekstremitet.
Ved å bruke kriteriet til det andre derivatet kan vi vite om et kritisk antall av en funksjon er et lokalt maksimum eller et minimum, uten å måtte se hva tegnet på funksjonen er i de nevnte intervallene..
Det andre driftskriteriet forteller oss at hvis f '(c) = 0 og at f "(x) er kontinuerlig i (a, b), skjer det at hvis f" (c)> 0 så er f (c) en lokal minimum og hvis f "(c) < 0 entonces f(c) es un máximo local.
Hvis f "(c) = 0, kan vi ikke konkludere med noe.
Eksempel
Gitt funksjonen f (x) = x4 + (4/3) x3 - 4xto, finn de relative maksima og minima av f ved å anvende det andre derivatkriteriet.
Først beregner vi f '(x) og f "(x), og vi har:
f '(x) = 4x3 + 4xto - 8x
f "(x) = 12xto + 8x - 8
Nå er f '(x) = 0 if, og bare hvis 4x (x + 2) (x - 1) = 0, og dette skjer når x = 0, x = 1 eller x = - 2.
For å avgjøre om de oppnådde kritiske tallene er relative ekstremer, er det nok å evaluere ved f "og dermed observere dens tegn.
f "(0) = - 8, så f (0) er et lokalt maksimum.
f "(1) = 12, så f (1) er et lokalt minimum.
f "(- 2) = 24, så f (- 2) er et lokalt minimum.
Taylor-serien
La f være en funksjon definert som følger:
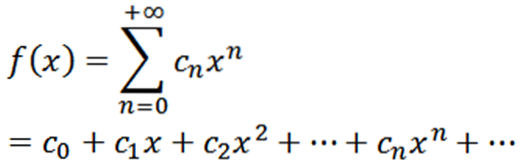
Denne funksjonen har en konvergensradius R> 0 og har derivater av alle ordrer i (-R, R). De etterfølgende derivatene av f gir oss:
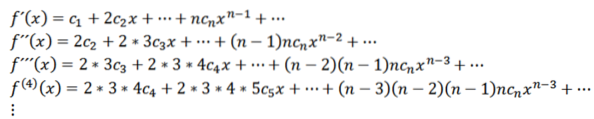
Tar vi x = 0, kan vi oppnå verdiene til cn basert på derivatene som følger:
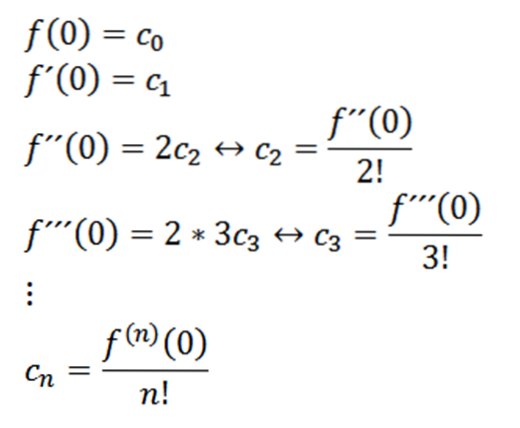
Hvis vi tar n = 0 som funksjonen f (det vil si f ^ 0 = f), kan vi omskrive funksjonen som følger:
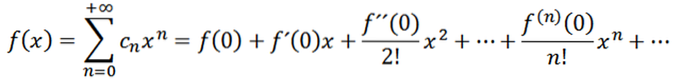
La oss nå vurdere funksjonen som en serie krefter ved x = a:
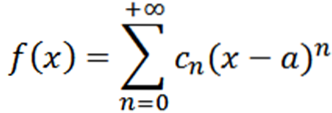
Hvis vi utfører en analyse som er analog med den forrige, vil vi ha at vi kan skrive funksjonen f som:
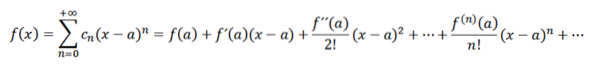
Disse seriene er kjent som Taylor-serien fra f til a. Når a = 0 har vi det spesielle tilfellet som kalles Maclaurin-serien. Denne typen serier er av stor matematisk betydning, spesielt i numerisk analyse, siden takket være disse kan vi definere funksjoner i datamaskiner som ex , sin (x) og cos (x).
Eksempel
Få Maclaurin-serien for ex.
Merk at hvis f (x) = ex, deretter f(n)(x) = ex og f(n)(0) = 1, så Maclaurin-serien din er:
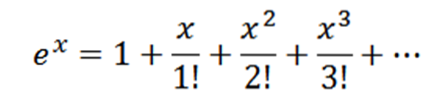
Referanser
- Frank Ayres, J. og Mendelson, E. (s.f.). Beregning 5ed. Mc Graw Hill.
- Leithold, L. (1992). Beregningen med analytisk geometri. HARLA, S.A.
- Purcell, E. J., Varberg, D., og Rigdon, S. E. (2007). Beregning. Mexico: Pearson Education.
- Saenz, J. (2005). Diferential calculus. Hypotenuse.
- Saenz, J. (s.f.). Integrert kalkulator. Hypotenuse.


Ingen har kommentert denne artikkelen ennå.