Additive dekomponeringsapplikasjoner, partisjoner, grafikk

De additiv nedbrytning av et positivt heltall er å uttrykke det som en sum av to eller flere positive heltall. Dermed har vi at tallet 5 kan uttrykkes som 5 = 1 + 4, 5 = 2 + 3 eller 5 = 1 + 2 + 2. Hver av disse måtene å skrive nummeret 5 er det vi vil kalle additiv nedbrytning.

Hvis vi følger med, kan vi se at uttrykkene 5 = 2 + 3 og 5 = 3 + 2 representerer samme sammensetning; de har begge samme tall. Imidlertid, bare for enkelhets skyld, skrives hvert av tilleggene vanligvis etter kriteriet fra laveste til høyeste.

Artikkelindeks

• 1 Additiv nedbrytning
• 2 Kanonisk additiv nedbrytning
• 3 applikasjoner
  • 3.1 Eksempelsetning
• 4 Skillevegger
  • 4.1 Definisjon
• 5 diagrammer
• 6 Referanser

Additiv nedbrytning

Som et annet eksempel kan vi ta tallet 27, som vi kan uttrykke som:

27 = 7 + 10 + 10

27 = 9 + 9 + 9

27 = 3 + 6 + 9 + 9

27 = 9 + 18

Additiv nedbrytning er et veldig nyttig verktøy som lar oss styrke vår kunnskap om nummereringssystemer.

Kanonisk additiv nedbrytning

Når vi har tall med mer enn to sifre, er en bestemt måte å spalte dem på i multiplene 10, 100, 1000, 10 000, etc., som utgjør det. Denne måten å skrive et hvilket som helst tall på kalles kanonisk additiv nedbrytning. For eksempel kan tallet 1456 spaltes som følger:

1456 = 1000 + 400+ 50 + 6

Hvis vi har tallet 20 846 295, vil dets kanoniske additiv nedbrytning være:

20 846 295 = 20 000 000 + 800 000 + 40 000 + 6000 + 200 + 90 +5.

Takket være denne nedbrytningen kan vi se at verdien til et gitt siffer er gitt av posisjonen den inntar. La oss ta tallene 24 og 42 som et eksempel:

24 = 20 + 4

42 = 40 +2

Her kan vi se at i 24 har 2 en verdi på 20 enheter og 4 en verdi på 4 enheter; derimot, i 42 har 4 en verdi på 40 enheter og 2 av to enheter. Så selv om begge tallene bruker de samme sifrene, er verdiene deres helt forskjellige på grunn av posisjonen de inntar.

applikasjoner

En av applikasjonene vi kan gi til additiv nedbrytning er i visse typer bevis, der det er veldig nyttig å se et positivt heltall som summen av andre.

Eksempel setning

La oss ta et eksempel på følgende setning med sine respektive bevis.

- La Z være et firesifret heltal, så kan Z deles med 5 hvis enhetsnummeret er null eller fem.

Demonstrasjon

La oss huske hva delbarhet er. Hvis vi har "a" og "b" heltall, sier vi at "a" deler "b" hvis det er et heltall "c" slik at b = a * c.

En av egenskapene til delbarhet forteller oss at hvis “a” og “b” er delbart med “c”, så er også subtraksjonen “a-b” delbar..

La Z være et firesifret heltall; derfor kan vi skrive Z som Z = ABCD.

Ved å bruke kanonisk additiv nedbrytning har vi:

Z = A * 1000 + B * 100 + C * 10 + D.

Det er klart at A * 1000 + B * 100 + C * 10 er delelig med 5. Av denne grunn har vi at Z er delelig med 5 hvis Z - (A * 1000 + B * 100 + C * 10) er delelig med 5.

Men Z - (A * 1000 + B * 100 + C * 10) = D og D er et ensifret tall, så den eneste måten å dele den med 5 er at den er 0 eller 5.

Derfor er Z delbart med 5 hvis D = 0 eller D = 5.

Merk at hvis Z har n sifre, er beviset nøyaktig det samme, det endrer bare at nå vil vi skrive Z = A₁TIL_to… TIL_n og målet ville være å bevise at A_n det er null eller fem.

Skillevegger

Vi sier at en partisjon av et positivt heltall er en måte som vi kan skrive et tall som en sum av positive heltall.

Forskjellen mellom en additiv nedbrytning og en partisjon er at mens den første søker at det i det minste kan spaltes i to tillegg eller mer, har partisjonen ikke denne begrensningen.

Dermed har vi følgende:

5 = 5

5 = 1 + 4

5 = 2 + 3

5 = 1 + 2 + 2

Ovennevnte er partisjoner på 5.

Det vil si at vi har at hver additiv nedbrytning er en partisjon, men ikke hver partisjon er nødvendigvis en additiv nedbrytning..

I tallteorien garanterer den grunnleggende setningen til aritmetikk at hvert heltall kan skrives unikt som et produkt av primtall.

Når du studerer partisjoner, er målet å bestemme på hvor mange måter et positivt heltall kan skrives som summen av andre heltall. Derfor definerer vi partisjonsfunksjonen som presentert nedenfor.

Definisjon

Partisjonsfunksjonen p (n) er definert som antall måter et positivt heltall n kan skrives som en sum av positive heltall.

Når vi går tilbake til eksemplet på 5, har vi det:

5 = 5

5 = 1 + 4

5 = 2 + 3

5 = 1 + 1 + 3

5 = 1 + 2 + 2

5 = 1 + 1 + 1 + 2

5 = 1 + 1 + 1 + 1 + 1

Dermed er p (5) = 7.

Kart

Både partisjoner og additive nedbrytninger av et tall n kan representeres geometrisk. Anta at vi har en additiv nedbrytning av n. I denne nedbrytningen kan tilleggene ordnes slik at medlemmene av summen blir ordnet fra det minste til det største. Så ok:

n = a₁ + til_to + til₃ +… + A_r med

til₁ ≤ a_to ≤ a₃ ≤… ≤ a_r.

Vi kan tegne en graf for denne dekomponeringen på følgende måte: i en første rad markerer vi a₁-poeng, så i det neste markerer vi_to-poeng, og så videre til du når en_r.

Ta for eksempel tallet 23 og dets nedbrytning:

23 = 5 + 4 + 7 + 3 + 1 +3

Vi bestiller denne nedbrytningen, og vi har:

23 = 1 + 3 + 3 + 4+ 5 + 7

Den tilsvarende grafen vil være:

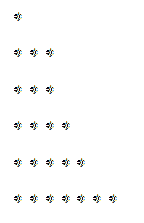
På samme måte, hvis vi leser nevnte graf vertikalt i stedet for horisontalt, kan vi oppnå en nedbrytning som muligens er forskjellig fra den forrige. I eksemplet på 23 skiller seg følgende ut:

Så vi har 23, vi kan også skrive det som:

23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.

Referanser

1. G.H. Hardy og E. M. Wright. En introduksjon til tallteori. Oxford Clarendon Press.
2. Navarro C. Didaktisk leksikon 6. Redaksjonell Santillana, S.A.
3. Navarro C.Lenke til matematikk 6. Redaksjonell Santillana, S.A.
4. Niven & Zuckerman. Innføring i tallteori. Limusa.
5. VV.AA Evaluering Kriterium for matematikkområdet: En modell for grunnskolen. Wolters Kluwer utdanning.
6. Didaktisk leksikon 6.