Gratis kroppsdiagram hvordan du gjør det, eksempler, trening

EN Free-Body diagram, isolert kroppsdiagram eller kraftdiagram, er et diagram der kreftene som virker på et legeme er representert av piler.

Sørg for å ta med i diagrammet alle kreftene som virker på objektet, og siden det er en vektormengde, har pilen ansvaret for å indikere retningen og sansen, mens lengden gir en ide om modul eller intensitet.

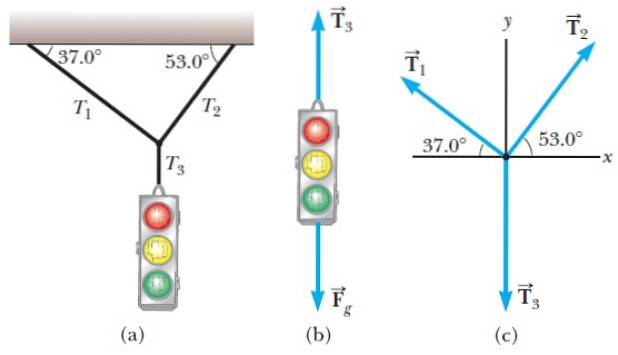
I figur 1 har vi et eksempel på et fritt kroppsdiagram som vi skal analysere.

Situasjonen er som følger: et trafikklys som henger i ro fra noen kabler (figur 1a). To krefter virker på den, den ene er den som utøves av jorden, som er vekt. I diagrammet er det betegnet som F_g og virker loddrett nedover.

Den andre kraften er spenningen i den vertikale strengen, kalt T₃ og som går i vertikal retning oppover, holder trafikklyset og forhindrer at det faller til bakken.

Når et problem har mer enn ett objekt, er det nødvendig å tegne et diagram for hver enkelt..

Knuten mellom de skrå tauene og tauet som holder trafikklyset betraktes som et punktobjekt, og frikroppsdiagrammet er i figur 1c. Merk at for knuten, spenningen T₃ er rettet nedover.

Det er viktig å merke seg at kreftene som utøves av objektet på andre legemer ikke skal vises i frikroppsdiagrammet, men bare de som handler på det.

Artikkelindeks

• 1 Eksempler på fritt kroppsdiagram
  • 1.1 En person som trekker en koffert eller container
  • 1.2 En blokk som glir nedover et skrått plan
  • 1.3 Atwoods maskin
• 2 Øvelsen løst
  • 2.1 Løsning
• 3 Referanser

Eksempler på fritt kroppsdiagram

Frikroppsdiagrammet tillater anvendelse av Newtons lover og med dem bestemmer bevegelsestilstanden eller resten av objektet som kreftene virker på. Når det gjelder trafikklyset som vises, kan vi bestemme verdien av spenningene i kablene som holder trafikklyset, og vite vekten av dette.

Når disse dataene er kjent, velges passende kabler for å henge trafikklyset og som oppfyller deres funksjon uten å kollapse.

Frikroppsdiagrammer brukes til å beskrive ulike hverdagssituasjoner, som disse:

En person som trekker en koffert eller container

Det er veldig vanlig at folk må bære tunge gjenstander som containeren på figuren. For å gjøre dette må de utøve en styrke F om containeren, som i dette eksemplet er vannrett og til høyre, som er bevegelsesretningen.

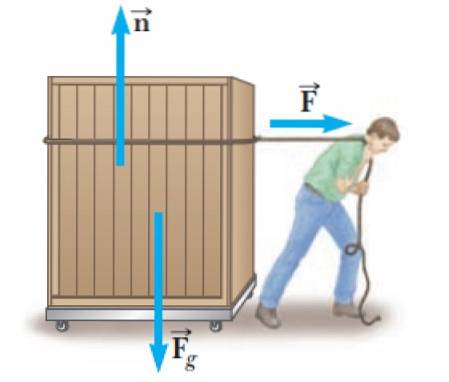
Men dette er ikke den eneste kraften som virker på ham, det er også det normale n, utøves av den flate overflaten på hjulplattformen. Og til slutt er det vekten av det: F_g, rettet vertikalt ned.

Det normale er en kraft som oppstår når to flater er i kontakt og alltid er vinkelrett på overflaten som utøver den. I dette tilfellet utøver hjulplattformen normal på containeren.

En blokk som glir nedover et skrått plan

Noen skrivebord har bordet litt vippet for å gjøre det lettere å ta notater og lese. Den har også en blyantspor, men vi har alle satt blyanten på bordet ut av sporet, og vi har sett hvordan den glir på bordet.

Hvilke krefter virker på blyanten?

De samme som virker på blokken vist i følgende frikroppsdiagram:

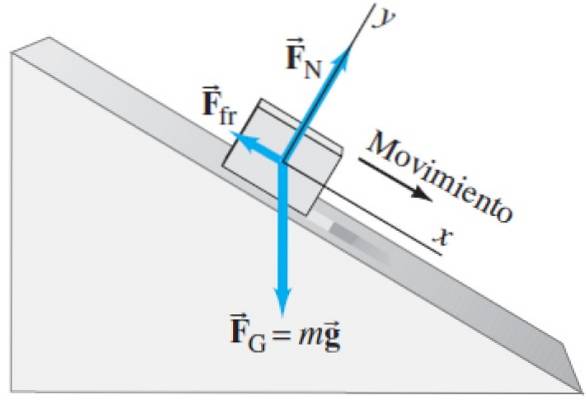
Det normale F_N er kraften som bordoverflaten utøver på den støttede blyanten eller blokken. I motsetning til forrige eksempel er det normale ikke vertikalt, men skrått. Husk at det normale er kraften som bordet utøver på blokken og er vinkelrett på den. Siden bordet er vippet, er det vanlige også.

Som alltid vekten F_g er loddrett, uavhengig av systemets tilbøyelighet.

Og til slutt har vi en ny kraft som virker, som er kinetisk friksjon F_fr mellom bordet og blyanten eller blokken. Friksjon er også en kontaktkraft, men i motsetning til normalt er den en tangensiell (parallell) kraft til overflaten. Legg også merke til at det alltid er rettet i motsatt retning av bevegelse..

Atwoods maskin

Atwood-maskinen er en enkel maskin som består av en lett, friksjonsfri remskive på skinnen, gjennom hvilken et lett og ikke-utvidbart tau passerer.

To gjenstander med masse m henges fra den₁ og M_to. Når en av gjenstandene går opp, går den andre ned, som vist i figur 4a:

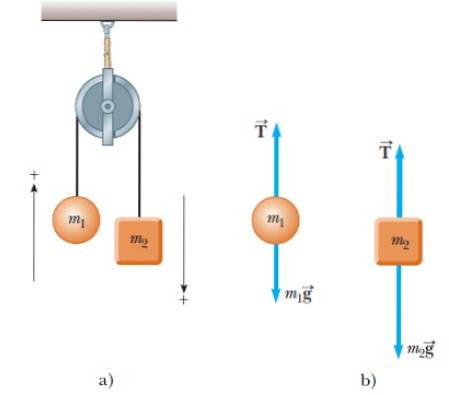
Siden det er to objekter, blir det laget et fritt kroppsdiagram for hver enkelt. For begge objektene er det bare to krefter: spenningen i strengen T og de respektive vektene.

I figuren uttrykkes hver vekt direkte som masseproduktet og akselerasjonen. På sin side er spenningen alltid rettet vertikalt langs det spente tauet.

Treningen løst

Bruk Newtons lover for å bestemme akselerasjonen som massene beveger seg fra Atwood-maskinen som vist i forrige avsnitt.

Løsning

Newtons andre lov sier at summen av kreftene er lik masseproduktet og akselerasjonen.

Tegnkonvensjonen i hver masse kan være forskjellig, så vi kommer til å ta bevegelse som en positiv følelse, som indikert i grafen, den første massen stiger og den andre faller.

I noen problemer gir utsagnet ikke informasjon, så må skiltene tildeles vilkårlig, og hvis resultatet av akselerasjonen er negativt, beveger massesystemet seg i motsatt retning til den opprinnelig antatte.

-For masse 1 (stiger):

T - m₁g = m₁til

-For masse 2 (lav):

-T + m_tog = m_totil

Begge ligningene danner et system med lineære ligninger av to ukjente, ettersom spenningen vises med et annet tegn i hver ligning, legger vi ganske enkelt til dem ord for ord og spenningen avbrytes:

m_tog - m₁g = m₁a + m_totil

a = m_tog - m₁g / (m₁ + m_to)

Referanser

1. Bauer, W. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
2. Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. Sjette. Ed prentice hall.
3. Serway, R., Vulle, C. 2011. College Physics. 9. utg. Cengage Learning.
4. Tipler, P. (2006) Fysikk for vitenskap og teknologi. 5. utg. Bind 1. Redaksjonell Reverté.
5. Tippens, P. 2011. Fysikk: Konsepter og applikasjoner. 7. utgave. Mcgraw hill