De forskjeller mellom hastighet og hastighet de eksisterer, selv om de begge er relaterte fysiske størrelser. På vanlig språk brukes det ene eller det andre begrepet om hverandre som om de var synonymer, men i fysikk er det nødvendig å skille mellom dem..
Denne artikkelen definerer begge begrepene, peker på forskjellene og forklarer ved hjelp av eksempler hvordan og når den ene eller den andre blir brukt. For å forenkle vurderer vi en partikkel i bevegelse, og derfra vil vi gå gjennom begrepene hastighet og hastighet.
| Hastighet | Hastighet | |
| Definisjon | Det er den tilbakelagte avstanden per tidsenhet. | Det er forskyvning (eller endring av posisjon) i hver tidsenhet. |
| Notasjon | v | v |
| Matematisk objekttype | Klatre. | Vector. |
| Formel (i en begrenset periode) * | v = Δs / Δt | v = Δr / Δt |
| Formel (for et gitt øyeblikk) ** | v = ds / dt = s '(t) | v = dr / dt = r '(t) |
| Forklaring av formelen | * Lengden på stien som er delt delt på tidsperioden som brukes til å reise den. ** I øyeblikkelig hastighet har tidsperioden en tendens til null. | * Vektorforskyvning delt på tidsperioden forskyvningen skjedde. |
| Kjennetegn | For å uttrykke det kreves bare et positivt reelt tall, uavhengig av de romlige dimensjonene bevegelsen skjer i.. | Det kan ta mer enn ett reelt tall (positivt eller negativt) for å uttrykke det, avhengig av de romlige dimensjonene der bevegelsen forekommer.. |
Ulike aspekter av hastighet og hastighet ble oppsummert i tabellen ovenfor. For å utfylle det, vurderes det flere eksempler som illustrerer begrepene og deres forhold:
Anta at en rød maur beveger seg langs en rett linje og i retningen som er angitt i figuren nedenfor.
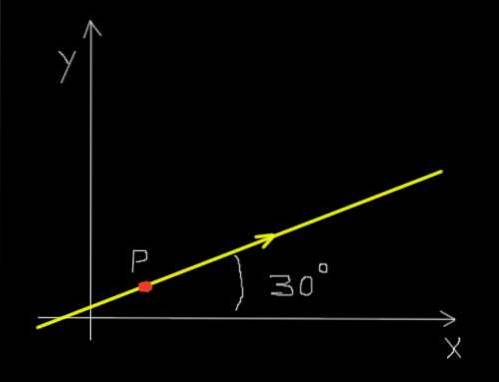
I tillegg beveger mauren seg jevnt på en slik måte at den beveger seg en avstand på 30 millimeter i løpet av en periode på 0,25 sekunder..
Bestem maurens hastighet og hastighet.
Maurens hastighet beregnes ved å dele avstanden Δs reiste mellom tidsforløpet At.
v = Δs / Δt = (30 mm) / (0,25 s) = 120 mm / s = 12 cm / s
Maurens hastighet beregnes ved å dele forskyvningen Δr mellom perioden da forskyvningen ble gjort.
Forskyvningen var 30 mm i 30 ° retning i forhold til X-aksen, eller i kompakt form:
Δr = (30 mm ¦ 30º)
Det kan bemerkes at forskyvningen består av en størrelse og en retning, siden det er en vektormengde. Alternativt kan forskyvningen uttrykkes i henhold til de kartesiske komponentene X og Y, på denne måten:
Δr = (30 mm * cos (30º); 30 mm * sin (30º)) = (25,98 mm; 15,00 mm)
Maurens hastighet beregnes ved å dele forskyvningen med tidsperioden den ble gjort:
v = Δr/ Δt = (25,98 mm / 0,25 sek; 15,00 mm / 0,25 sek) = (103,92; 60,00) mm / sek
Denne hastigheten i kartesiske komponenter X og Y og i enheter på cm / s er:
v = (10.392; 6.000) cm / s.
Alternativt kan hastighetsvektoren uttrykkes i sin polære form (modul ¦ retning) som vist:
v = (12 cm / s ¦ 30º).
Merk: i dette eksemplet, siden hastigheten er konstant, faller gjennomsnittshastigheten og den øyeblikkelige hastigheten sammen. Modulen for øyeblikkelig hastighet er funnet å være øyeblikkelig hastighet.
Den samme mauren i forrige eksempel går fra A til B, deretter fra B til C og til slutt fra C til A, etter den trekantede banen vist i følgende figur.
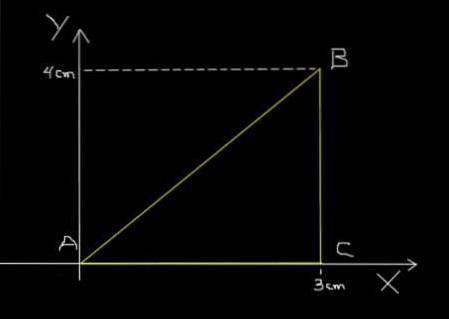
Seksjon AB dekker det i 0,2 sek. BC går gjennom den på 0,1 sek og til slutt kjører CA gjennom den på 0,3 sek. Beregn gjennomsnittshastigheten for turen ABCA og gjennomsnittshastigheten for turen ABCA.
For å beregne gjennomsnittsfarten til mauren begynner vi med å bestemme den totale tilbakelagte distansen:
Δs = 5 cm + 4 cm + 3 cm = 12 cm.
Tidsrommet som brukes for hele reisen er:
Δt = 0,2 s + 0,1 s + 0,3 s = 0,6 s.
Så, den gjennomsnittlige hastigheten til mauren er:
v = Δs / Δt = (12 cm) / (0,6 s) = 20 cm / s.
Deretter beregnes maurens gjennomsnittshastighet i ABCA-ruten. I dette tilfellet er forskyvningen som mauren gjør:
Δr = (0 cm; 0 cm)
Dette er fordi forskyvningen er forskjellen mellom sluttposisjon minus startposisjon. Siden begge posisjonene er like, er forskjellen null, noe som resulterer i en null forskyvning.
Denne nullforskyvningen ble utført i en periode på 0,6 sek, så gjennomsnittshastigheten til mauren var:
v =(0 cm; 0 cm) / 0,6 s = (0; 0) cm / s.
Konklusjon: gjennomsnittshastighet 20 cm / s, men gjennomsnittshastigheten er null i ABCA-ruten.
Et insekt beveger seg på en sirkel med en radius på 0,2 m med jevn hastighet, slik at den, startende fra A og ankommer B, beveger seg ¼ med en omkrets på 0,25 s.
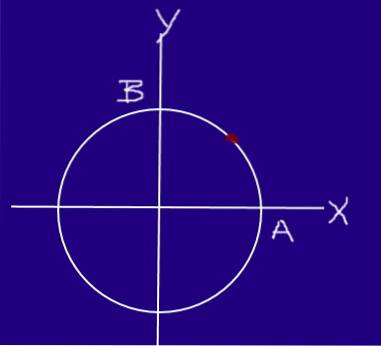
Bestem hastigheten og hastigheten til insektet i seksjon AB.
Lengden på omkretsbuen mellom A og B er:
Δs = 2πR / 4 = 2π (0,2 m) / 4 = 0,32 m.
Ved å bruke definisjonen av gjennomsnittshastighet har vi:
v = Δs / Δt = 0,32 m / 0,25 s = 1,28 m / s.
For å beregne gjennomsnittshastigheten er det nødvendig å beregne forskyvningsvektoren mellom utgangsposisjonen A og sluttposisjon B:
Δr = (0, R) - (R, 0) = (-R, R) = (-0,2, 0,2) m
Ved å bruke definisjonen av gjennomsnittshastighet får vi:
v = Δr/ Δt = (-0,2, 0,2) m / 0,25 s = (-0,8, 0,8) m / s.
Det forrige uttrykket er gjennomsnittshastigheten mellom A og B uttrykt i kartesisk form. Alternativt kan gjennomsnittshastigheten uttrykkes i polær form, det vil si modul og retning:
| v | = ((-0,8) ^ 2 + 0,8 ^ 2) ^ (½) = 1,13 m / s
Retning = arctan (0,8 / (-0,8)) = arctan (-1) = -45º + 180º = 135 ° i forhold til X-aksen.
Til slutt er den gjennomsnittlige hastighetsvektoren i polar form: v =(1,13 m / s ¦ 135º).
Forutsatt at starttiden for insektet i forrige eksempel er 0s fra punkt A, har vi at dets posisjonsvektor når som helst t er gitt av:
r(t) = [R cos ((π / 2) t); R sin ((π / 2) t)].
Bestem hastighet og øyeblikkelig hastighet for ethvert øyeblikkelig t.
Den øyeblikkelige hastigheten er avledet med hensyn til posisjonens funksjonstid:
v(t) = dr/ dt = [-R (π / 2) sin ((π / 2) t); R (π / 2) cos ((π / 2) t)]
Den øyeblikkelige hastigheten er modulen til den øyeblikkelige hastighetsvektoren:
v (t) = | v(t) | = π R / 2 ^ ½
Ingen har kommentert denne artikkelen ennå.