
Overflatedilatasjonsformel, koeffisienter og eksempler
De overfladisk utvidelse Det er utvidelsen som oppstår når et objekt opplever variasjoner i overflaten på grunn av en variasjon i temperaturen. Det skyldes materialets egenskaper eller geometriske form. Utvidelsen dominerer i to dimensjoner i samme proporsjon.
For eksempel i et ark, når det er en endring i temperatur, er det overflaten på arket som gjennomgår den største endringen på grunn av termisk ekspansjon..

Metallplaten i forrige figur øker bredden og lengden betydelig når den varmes opp av solstråling. Tvert imot, begge reduseres betydelig når den avkjøles på grunn av en reduksjon i omgivelsestemperaturen..
Det er av denne grunn at når fliser installeres på et gulv, bør ikke kantene klebe seg sammen, men det bør være et gap som kalles en ekspansjonsfuge..
I tillegg er dette rommet fylt med en spesiell blanding som har en viss grad av fleksibilitet, og forhindrer at flisene sprekker på grunn av det sterke trykket som termisk ekspansjon kan gi..
Artikkelindeks
- 1 Hva er overfladisk utvidelse?
- 2 Overflatedilatasjon og dens koeffisient
- 3 Koeffisient for overflateutvidelse for forskjellige materialer
- 4 Arbeidseksempler på overflateutvidelse
- 4.1 Eksempel 1
- 4.2 Eksempel 2
- 5 Referanser
Hva er overfladisk utvidelse?
I et fast materiale opprettholder atomene sine relative posisjoner mer eller mindre faste rundt et likevektspunkt. På grunn av termisk omrøring svinger de imidlertid alltid rundt det samme.
Når temperaturen øker, øker også den termiske svingningen, noe som får de midterste svingningsposisjonene til å endres. Dette er fordi bindingspotensialet ikke er akkurat parabolsk og har asymmetri rundt minimum.
Nedenfor er en figur som skisserer den kjemiske bindingsenergien som en funksjon av den interatomiske avstanden. Den totale svingningsenergien ved to temperaturer og hvordan svingningssenteret beveger seg, er også vist..
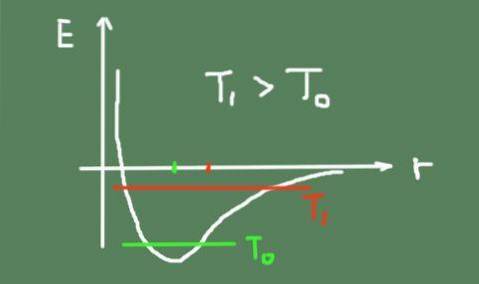
Overfladisk utvidelse og dens koeffisient
For å måle overflatedilatasjonen starter vi fra et innledende område A og en utgangstemperatur T av objektet hvis utvidelse skal måles..
Anta at objektet er et ark av område A, og dets tykkelse er mye mindre enn kvadratroten av område A. Arket blir utsatt for en temperaturvariasjon AT, slik at dets endelige temperatur når den termiske likevekten med varmekilden har vært etablert, vil det være T '= T + ΔT.
Under denne termiske prosessen vil overflatearealet også ha endret seg til en ny verdi A '= A + ΔA, hvor ΔA er endringen i lengde. Dermed er koeffisienten for overflateutvidelse σ definert som kvotienten mellom den relative variasjonen av areal per enhet av temperaturvariasjon.
Følgende formel definerer koeffisienten for overflateutvidelse σ:
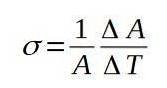
Koeffisienten for overflateutvidelse σ er praktisk talt konstant over et bredt spekter av temperaturverdier.
Ved definisjonen av σ er dimensjonene invers av temperaturen. Enheten er vanligvis ° C-1.
Koeffisient for overflateutvidelse for forskjellige materialer
Deretter vil vi gi en liste over koeffisienten for overfladisk utvidelse for noen materialer og elementer. Koeffisienten beregnes ved normalt atmosfæretrykk basert på en omgivelsestemperatur på 25 ° C, og verdien blir betraktet som konstant i et område på AT fra -10 ° C til 100 ° C.
Enheten til overflateutvidelseskoeffisienten vil være (° C)-1
- Stål: σ = 24 ∙ 10-6 (° C)-1
- Aluminium: σ = 46 ∙ 10-6 (° C)-1
- Gull: σ = 28 ∙ 10-6 (° C)-1
- Kobber: σ = 34 ∙ 10-6 (° C)-1
- Messing: σ = 36 ∙ 10-6 (° C)-1
- Jern: σ = 24 ∙ 10-6 (° C)-1
- Glass: σ = (14 til 18) ∙ 10-6 (° C)-1
- Kvarts: σ = 0,8 ∙ 10-6 (° C)-1
- Diamant: σ = 2 ,, 4 ∙ 10-6 (° C)-1
- Bly: σ = 60 ∙ 10-6 (° C)-1
- Eiketre: σ = 108 ∙ 10-6 (° C)-1
- PVC: σ = 104 ∙ 10-6 (° C)-1
- Karbonfiber: σ = -1,6 ∙ 10-6 (° C)-1
- Betong: σ = (16 til 24) ∙ 10-6 (° C)-1
De fleste materialer strekker seg med temperaturøkning. Imidlertid krymper noen materialer som karbonfiber med økende temperatur..
Arbeidet eksempler på overflateutvidelse
Eksempel 1
En stålplate har dimensjoner på 3m x 5m. Om morgenen og i skyggen er temperaturen 14 ° C, men ved middagstid varmer solen opp til 52 ° C. Finn det siste området på platen.
Løsning
Vi starter fra definisjonen av koeffisienten for overflateutvidelse:
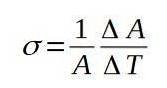
Herfra løser vi variasjonen i området:
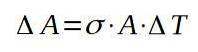
Vi fortsetter deretter med å erstatte de respektive verdiene for å finne økningen i areal med økningen i temperatur.
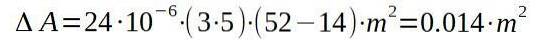
Det vil si at det endelige arealet vil være 15.014 kvadratmeter.
Eksempel 2
Vis at koeffisienten for overflateutvidelse er omtrent det dobbelte av koeffisienten for lineær ekspansjon.
Løsning
Anta at vi starter fra en rektangulær plate med dimensjonene bredde Lx og lengde Ly, så blir dens opprinnelige areal A = Lx ∙ Ly
Når platen gjennomgår en temperaturøkning ΔT, øker også dimensjonene den nye bredden Lx 'og den nye lengden Ly', slik at det nye området blir A '= Lx' ∙ Ly '

Variasjonen som påføres området av platen på grunn av endring i temperatur vil da være
ΔA = Lx '∙ Ly' - Lx ∙ Ly
hvor Lx '= Lx (1 + α ΔT) og Ly' = Ly (1 + α ΔT)
Det vil si at endringen i område som en funksjon av koeffisienten for lineær ekspansjon og temperaturendringen vil være:
ΔA = Lx (1 + α ΔT) ∙ Ly (1 + α ΔT) - Lx ∙ Ly
Dette kan skrives om som:
ΔA = Lx ∙ Ly ∙ (1 + α ΔT) ² - Lx ∙ Ly
Ved å utvikle firkanten og multiplisere har vi følgende:
ΔA = Lx ∙ Ly + 2α ΔT Lx ∙ Ly + (α ΔT) ² Lx ∙ Ly - Lx ∙ Ly
Siden α er i størrelsesorden 10-6, når den er kvadratisk, er den i størrelsesorden 10-12. Dermed er det kvadratiske begrepet i ovennevnte uttrykk ubetydelig.
Da kan arealøkningen tilnærmes med:
ΔA ≈ 2α ΔT Lx ∙ Ly
Men arealøkningen som en funksjon av overflateutvidelseskoeffisienten er:
ΔA = γ ΔT A
Fra hvilket et uttrykk er avledet som relaterer koeffisienten for lineær ekspansjon med koeffisienten for overflatexpansjon.
γ ≈ 2 ∙ α
Referanser
- Bauer, W. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mac Graw Hill. 422-527
- Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. Sjette. Utgave. Prentice Hall. 238-249.



Ingen har kommentert denne artikkelen ennå.