
Diametersymboler og formler, hvordan du får det, omkrets
De diameter Det er den rette linjen som går gjennom sentrum av en lukket flat kurve eller en figur i to eller tre dimensjoner, og som også forbinder de motsatte punktene. Vanligvis er det en omkrets (en flat kurve), en sirkel (en flat figur), en kule eller en høyre sirkulær sylinder (tredimensjonale gjenstander).
Selv om omkrets og sirkel vanligvis blir tatt som synonymer, er det forskjell mellom de to begrepene. Omkretsen er den lukkede kurven som omslutter sirkelen, som oppfyller betingelsen om at avstanden mellom et av punktene og sentrum er den samme. Denne avstanden er ingen ringere enn omkretsens radius. I stedet er sirkelen en plan figur avgrenset av omkretsen.

Når det gjelder omkrets, sirkel og kule, er diameteren et rett segment som inneholder minst tre punkter: sentrum pluss to punkter på kanten av omkretsen eller sirkelen, eller overflaten til kule.
Og når det gjelder den høyre sirkulære sylinderen, refererer diameteren til tverrsnittet, som sammen med høyden er de to karakteristiske parametrene.
Diameteren på omkretsen og sirkelen, symbolisert med ø eller ganske enkelt bokstaven "D" eller "d", er relatert til omkretsen, konturen eller lengden, som er betegnet med bokstaven L:
L = π.D = π. eller
Så lenge det er en omkrets, er kvotienten mellom lengden og diameteren det irrasjonelle tallet π = 3.14159 ..., på denne måten:
π = L / D
Artikkelindeks
- 1 Hvordan få diameteren?
- 1.1 Figurer med konstant bredde
- 2 Diameter på en sirkel
- 2.1 - Eksempel 1
- 2.2 - Eksempel 2
- 3 Hvor mange diametre har en omkrets?
- 4 Referanser
Hvordan få diameteren?
Når du har tegningen av omkretsen eller sirkelen, eller direkte den sirkulære gjenstanden, for eksempel en mynt eller en ring, er det veldig enkelt å finne diameteren med en linjal. Du må bare sørge for at linjekanten berører to punkter på omkretsen og midten av den samtidig..
En tykkelse, vernier eller tykkelse er veldig egnet for måling av ytre og indre diameter på mynter, bøyler, ringer, muttere, rør og mer..

Hvis det i stedet for objektet eller tegningen er data som radius R, deretter multiplisere med 2 har vi diameteren. Og hvis omkretsens lengde eller omkrets er kjent, kan diameteren også være kjent ved å fjerne:
D = 2.R
D = L / π
En annen måte å finne diameteren på er å kjenne sirkelområdet, den sfæriske overflaten, tverrsnittet til sylinderen, det buede området til sylinderen eller volumene til sfæren eller sylinderen. Alt avhenger av hvilken geometrisk figur det er. For eksempel er diameter involvert i følgende områder og volumer:
-Sirkelområde: π. (D / 2)to
-Sfærisk overflate: 4π. (D / 2)to
-Kuleens volum: (4/3) π. (D / 2)3
-Høyre sirkulært sylindervolum: π. (D / 2)to.H (H er høyden på sylinderen)
Figurer med konstant bredde
Sirkelen er en flat figur med konstant bredde, siden hvor enn du ser på den, er bredden diameteren D. Imidlertid er det andre kanskje mindre kjente figurer hvis bredde også er konstant..
La oss først se hva som forstås av bredden på en figur: det er avstanden mellom to parallelle linjer - støttelinjer - som igjen er vinkelrett på den gitte retningen og som fanger figuren, som vist på venstre bilde:
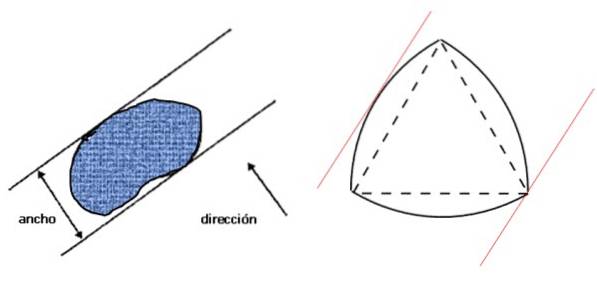
Ved siden av høyre er Reuleaux-trekanten, som er en figur med konstant bredde og som oppfyller betingelsen spesifisert i venstre figur. Hvis bredden på figuren er D, er omkretsen gitt av Barbiers teorem:
L = π.D
Kloakkene til byen San Francisco i California er formet som en Reuleaux-trekant, oppkalt etter den tyske ingeniøren Franz Reuleaux (1829 - 1905). På denne måten kan ikke dekslene falle gjennom hullet, og mindre materiale brukes til å lage dem, siden området deres er mindre enn sirkelens:
A = (1 - 3) .πDto = 0,705.Dto
Mens du er i en sirkel:
A = π. (D / 2)to = (π / 4) Dto= 0.785.Dto
Men denne trekanten er ikke den eneste figuren med konstant bredde. Du kan bygge den såkalte Reuleaux polygoner med andre polygoner som har et ulikt antall sider.
Diameter på en omkrets

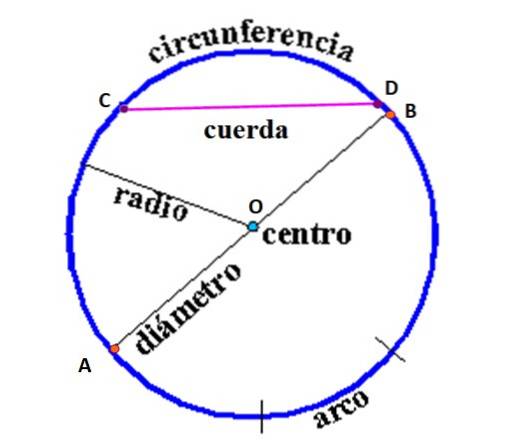
I neste figur er elementene i omkretsen, definert som følger:
String: linjesegment som forbinder to punkter på omkretsen. I figuren er akkorden som sammenføyer punkt C og D, men uendelige akkorder kan tegnes som forbinder et hvilket som helst par punkter på omkretsen.
Diameter: det er akkorden som går gjennom sentrum, og forbinder to punkter av omkretsen med sentrum O. Det er den lengste akkorden av en omkrets, av den grunn kalles den "major akkord".
Radio: linjesegment som forbinder sentrum med et hvilket som helst punkt på omkretsen. Verdien, som diameteren, er konstant.
Omkrets: er settet med alle punkter like langt fra O.
Bue: definert som et omkretssegment avgrenset av to radier (ikke tegnet i figuren).
- Eksempel 1
Det viste rektangelet er 10 tommer høyt, som når det er rullet danner en høyre sirkulær sylinder hvis diameter er 5 tommer. Svar på følgende spørsmål:
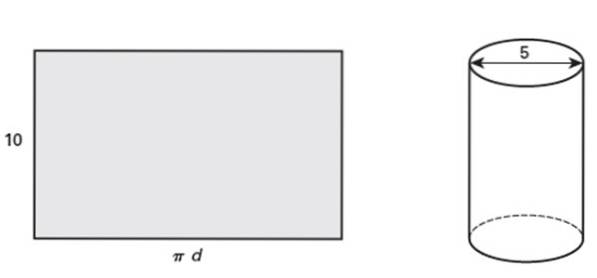
a) Hva er rørets kontur?
b) Finn området til rektangelet
c) Beregn tverrsnittsarealet til sylinderen.
Løsning til
Rørets omriss er L = π.D = 5π in = 15,71 in.
Løsning b
Arealet til rektangelet er base x høyde, å være basen L som allerede er beregnet og høyden er 10 inches i henhold til uttalelsen, derfor:
A = 15,71 x 10 in = 157,1 into.
Løsning c
Til slutt beregnes det etterspurte området slik:
A = π. (D / 2)to = (π / 4) Dto = (π / 4) x (5 tommer)to= 19,63 tommerto.
- Eksempel 2
Beregn det skyggelagte området i figur 5a. Torget har side L.
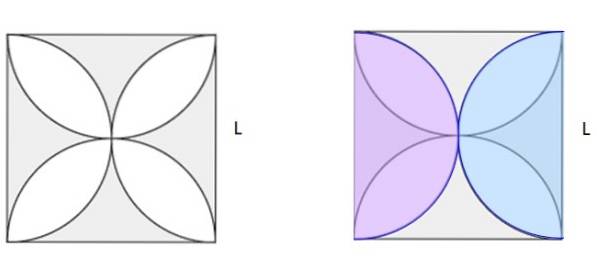
Løsning
I figur 5b er to halvsirkler av samme størrelse tegnet i rosa og blått, lagt på den opprinnelige figuren. Mellom dem lager de en komplett sirkel. Hvis du finner kvadratområdet og trekker sirkelområdet, lager du det skyggelagte området i figur 5b. Og når man ser nøye, viser det seg at det er halvparten av det skyggelagte området i 5a.
-Firkantet område: Lto
-Halvsirkel Diameter: L
-Sirkelområde: π. (L / 2)to= (π / 4) Lto
-Forskjell på områder = halvparten av det skyggelagte området =
Lto - (π / 4) Lto = [(4 - π) / 4] L.to= 0,2146 Lto
-Skyggelagt område = 2 x 0,2146 Lto= 0,4292L2
Hvor mange diametre har en omkrets?
Uendelige diametre kan tegnes på en omkrets, og noen av dem måler det samme.
Referanser
- Antonio. Reuleaux-trekanter og andre kurver med konstant bredde. Gjenopprettet fra: divulgators.com.
- Baldor, A. 2002. Plane and Space Geometry and Trigonometry. Patria Cultural Group.
- Jiménez, R. Mathematics II. Geometri og trigonometri. 2. plass. Utgave. Pearson.
- Wikipedia. Reuleaux-trekanten. Gjenopprettet fra: es.wikipedia.org.
- Wolfram MathWorld. Diameter. Gjenopprettet fra: mathworld.wolfram.com.



Ingen har kommentert denne artikkelen ennå.