Felles faktor ved gruppering av begrepseksempler, øvelser

De felles faktor ved gruppering av termer er en algebraisk prosedyre som lar deg skrive noen algebraiske uttrykk i form av faktorer. For å oppnå dette målet er det først nødvendig å gruppere uttrykket på riktig måte og observere at hver gruppe som således dannes faktisk har en felles faktor.

Å bruke teknikken riktig krever litt øvelse, men på kort tid kan du mestre den. La oss først se på et illustrerende eksempel beskrevet trinnvis. Da kan leseren bruke det de har lært i hver av øvelsene som kommer senere.

Anta for eksempel at du må faktorere følgende uttrykk:

2x^to + 2xy - 3zx - 3zy

Dette algebraiske uttrykket består av 4 monomier eller termer, atskilt med + og - tegn, nemlig:

2x^to, 2xy, -3zx, -3zy

Ser vi nøye på, er x vanlig for de tre første, men ikke de siste, mens y er vanlig for den andre og fjerde, og z er felles for den tredje og fjerde..

Så i prinsippet er det ingen felles faktor for de fire begrepene samtidig, men hvis de er gruppert som vist i neste avsnitt, er det mulig at en vil vises som hjelper til med å skrive uttrykket som produktet av to eller flere faktorer.

Artikkelindeks

• 1 Eksempler
• 2 Viktige spørsmål om felles faktor ved gruppering
• 3 Øvelser
  • 3.1 - Øvelse 1
  • 3.2 - Øvelse 2
• 4 Referanser

Eksempler

Faktoruttrykk: 2x^to + 2xy - 3zx - 3zy

Trinn 1: Gruppe

2x^to + 2xy - 3zx - 3zy = (2x^to + 2xy) + (-3zx - 3zy)

Trinn 2: Finn den felles faktoren til hver gruppe

2x^to + 2xy - 3zx - 3zy =

= (2x^to + 2xy) - (3zx + 3zy) =

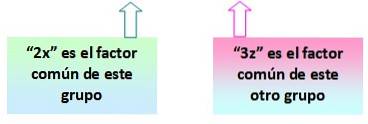
= 2x (x + y) - 3z (x + y)

Jegviktig: det negative tegnet det er også en felles faktor som må tas i betraktning.

Legg merke til at parentesene (x + y) gjentas i de to begrepene som oppnås ved gruppering. Det er den vanlige faktoren det ble søkt etter.

Trinn 3: Faktor hele uttrykket

2x^to + 2xy - 3zx - 3zy = (x + y) (2x - 3z)

Med det forrige resultatet er målet med faktorisering nådd, som er ingen ringere enn å transformere et algebraisk uttrykk basert på tillegg og subtraksjoner av termer, til produktet av to eller flere faktorer, i vårt eksempel, av: (x + y) y (2x - 3z).

Viktige spørsmål om felles faktor ved gruppering

Utgave 1: Hvordan vite at resultatet er riktig?

Svar: Den fordelende egenskapen brukes på det oppnådde resultatet, og etter å ha redusert og forenklet, må uttrykket som oppnås på den måten matche originalen, hvis ikke, er det en feil.

I forrige eksempel jobber vi i motsatt retning med resultatet for å kontrollere at det er riktig:

(x + y) (2x - 3z) = 2x^to -3zx + 2xy - 3zy

Ettersom rekkefølgen på tilleggene ikke endrer summen, returneres alle opprinnelige vilkår etter bruk av distribusjonsegenskapen, inkludert tegn, derfor er faktoriseringen riktig.

Spørsmål 2: Kunne det ha blitt gruppert på en annen måte?

Svar: Det er algebraiske uttrykk som tillater mer enn en form for gruppering og andre som ikke gjør det. I det valgte eksemplet kan leseren prøve andre muligheter alene, for eksempel å gruppere slik:

2x^to + 2xy - 3zx - 3zy = (2x^to- 3zx) + (2xy - 3zy)

Og du kan sjekke at resultatet er det samme som det ble oppnådd her. Å finne den optimale grupperingen er et spørsmål om praksis.

Spørsmål 3: Hvorfor er det nødvendig å ta en felles faktor fra et algebraisk uttrykk?

Svar: Fordi det er applikasjoner der det fakturerte uttrykket gjør beregningene enklere. Anta for eksempel at du vil gjøre 2x^to + 2xy - 3zx - 3zy lik 0. Hva ville være mulighetene?

For å svare på dette spørsmålet er den fakturerte versjonen mye mer nyttig enn den opprinnelige utviklingen. Det heter slik:

(x + y) (2x - 3z) = 0

En mulighet for at uttrykket er 0 er at x = -y, uavhengig av verdien av z. Og den andre er at x = (3/2) z, uavhengig av verdien av y.

Opplæring

- Øvelse 1

Ta en felles faktor i følgende uttrykk ved å gruppere termer:

øks + ay + bx + av

Løsning

De to første er gruppert, med den felles faktoren "a" og de to siste med den felles faktoren "b":

ax + ay + bx + by = a (x + y) + b (x + y)

Når dette er gjort, avsløres en ny felles faktor, som er (x + y), slik at:

ax + ay + bx + av = a (x + y) + b (x + y) = (x + y) (a + b)

En annen måte å gruppere på

Dette uttrykket støtter en annen måte å gruppere på. La oss se hva som skjer hvis ordene omorganiseres og en gruppe er laget med de som inneholder x og en annen med de som inneholder y:

ax + ay + bx + by = ax + bx + ay + by = x (a + b) + y (a + b)

På denne måten er den nye felles faktoren (a + b):

ax + ay + bx + by = ax + bx + ay + by = x (a + b) + y (a + b) = (x + y) (a + b)

Noe som fører til det samme resultatet fra den første grupperingen som ble testet.

- Øvelse 2

Følgende algebraiske uttrykk må skrives som et produkt av to faktorer:

3.³ - 3.^tob + 9ab^to-til^to+ab-3b^to

Løsning

Dette uttrykket inneholder 6 termer. La oss prøve å gruppere første og fjerde, andre og tredje og til slutt femte og sjette:

3.³ - 3.^tob + 9ab^to-til^to+ab-3b^to = (3a³ -til^to) + (- 3a^tob + 9ab^to) + (ab-3b^to)

Nå er hver parentes fakturert:

= (3a³ -til^to) + (- 3a^tob + 9ab^to) + (ab -3b^to) = a^to (3a - 1) + 3ab (3b -a) + b (a-3b)

Ved første øyekast ser det ut til at situasjonen har vært komplisert, men leseren skal ikke bli motløs, siden vi skal skrive om siste termin:

til^to (3a - 1) + 3ab (3b -a) + b (a-3b) = a^to (3a - 1) + 3ab (3b-a) - b (3b-a)

De to siste begrepene har nå en felles faktor, som er (3b-a), slik at de kan beregnes. Det er veldig viktig å ikke miste synet av første periode^to (3a - 1), som må fortsette å følge med alt som å legge til, selv om du ikke jobber med det:

til^to (3a - 1) + 3ab (3b-a) - b (3b-a) = a^to (3a - 1) + (3b-a) (3ab-b)

Uttrykket er redusert til to termer og en ny felles faktor blir oppdaget i den siste, som er "b". Nå gjenstår det:

til^to (3a - 1) + (3b-a) (3ab-b) = a^to (3a - 1) + b (3b-a) (3a-1)

Den neste vanlige faktoren som skal vises er 3a - 1:

til^to (3a - 1) + b (3b-a) (3a-1) = (3a - 1) [a^to + b (3b-a)]

Eller hvis du foretrekker uten parentes:

(3a - 1) [a^to + b (3b-a)] = (3a - 1) (a^to -ab + 3b^to)

Kan leseren finne en annen måte å gruppere på som fører til det samme resultatet??

Referanser

1. Baldor, A. 1974. Elementær algebra. Cultural Venezolana S.A.
2. Jiménez, R. 2008. Algebra. Prentice hall.
3. Hovedtilfeller av factoring. Gjenopprettet fra: julioprofe.net.
4. UNAM. Grunnleggende matematikk: Faktorisering ved gruppering av termer. Fakultet for regnskap og administrasjon.
5. Zill, D. 1984. Algebra og trigonometri. MacGraw Hill.