
Statisk friksjonskoeffisient, eksempel, trening

De statisk friksjon er kraften som oppstår mellom to flater når den ene overflaten ikke glir i forhold til den andre. Det er av stor betydning, siden det gjør at vi kan gå fremover når vi går, siden det er kraften som er tilstede mellom gulvet og skoens såle.
Det er også statisk friksjon som dukker opp mellom fortauet og bilens dekk. Hvis denne kraften ikke er tilstede, er det umulig for bilen å begynne å bevege seg, slik det skjer i en bil som prøver å starte på en isete overflate: hjulene glir, men bilen beveger seg ikke.

Statisk friksjon avhenger av ruheten til overflatene i kontakt og også av typen materiale de er laget av. Derfor er dekkene og sportsskoene laget av gummi for å øke friksjonen med fortauet..
I den statiske friksjonsmodellen er materialets egenskaper og graden av ruhet mellom overflatene oppsummert i et nummer kalt statisk friksjonskoeffisient, som bestemmes eksperimentelt.
Artikkelindeks
- 1 Koeffisient for statisk friksjon
- 2 Eksempel: bestemmelse av den statiske friksjonskoeffisienten
- 3 Trening
- 3.1 Løsning
- 4 Referanser
Statisk friksjonskoeffisient

Figuren over viser en bok som ligger i ro på et bord som har en helning på 15,7º.
Hvis overflatene på boken og bordet var veldig glatte og polerte, kunne ikke boka stå stille. Men siden de ikke er det, vises en kraft som er tangent til overflatene i kontakt som kalles kraften til statisk friksjon.
Hvis hellingsvinkelen er stor nok, er det ikke nok statisk friksjonskraft for å balansere boka, og den ville begynne å gli.
I dette tilfellet er det også friksjon mellom boken og bordet, men det ville være en styrke av dynamisk friksjon, også kalt kinetisk friksjon.
Det er en grense mellom statisk friksjon og dynamisk friksjon, som oppstår når den statiske friksjonen når sin maksimale verdi.
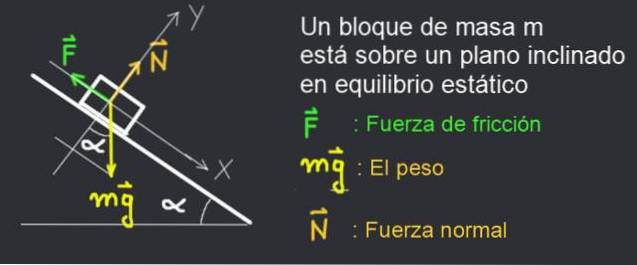
La oss se på figur 2, kraftdiagrammet til en massebok m som holdes i ro på et hellingsplan α.
Boken er i ro fordi den statiske friksjonskraften F balanserer systemet.
Hvis hellingsvinkelen øker litt, må overflatene i kontakt gi mer friksjonskraft, men mengden statisk friksjon som overflatene i kontakt kan gi har en maksimumsgrense Fmaks, nemlig:
F ≤ Fmaks.
Maksimal statisk friksjonskraft vil avhenge av materialene og ruhetsgraden til overflatene i kontakt, samt grepet på grepet.
Den statiske friksjonskoeffisienten μog er et positivt tall som avhenger av egenskapene til overflatene i kontakt. Normal kraft N som flyet utøver på blokken, viser graden av tetthet mellom blokkens overflate og planet. Slik bestemmer de den maksimale friksjonskraften som overflatene gir når det ikke glir:
Fmaks = μog N
Oppsummert følger den statiske friksjonskraften følgende modell:
F ≤ μog N
Eksempel: bestemmelse av den statiske friksjonskoeffisienten
Den statiske friksjonskoeffisienten er et dimensjonsløst tall som bestemmes eksperimentelt for hvert overflatepar.
Vi betrakter blokken i ro i figur 2. Følgende krefter virker på den:
- Friksjonskraft: F
- Vekten av masseblokken m: mg
- Normal kraft: N
Ettersom blokken er i ro og ikke har noen akselerasjon, ifølge Newtons andre lov, er den resulterende kraften - en vektorsum - null:
F + N + mg = 0
Et fast XY-koordinatsystem vurderes med X-aksen langs det skråplanet og Y-aksen vinkelrett på det, som vist i figur 2.
Kreftene må skilles fra hverandre i henhold til deres kartesiske komponenter, noe som gir opphav til følgende ligningssystem:
-Komponent X: -F + mg Sen (a) = 0
-Komponent Y: N - mg Cos (α) = 0
Verdien av den statiske friksjonskraften løses fra den første ligningen:
F = mg Sen (α)
Og fra det andre verdien av den normale kraften:
N = mg Cos (α)
Den statiske friksjonskraften F overholder følgende modell:
F ≤ μog N
Å erstatte tidligere oppnådde verdier i ulikheten vi har:
mg Sen (α) ≤ μog mg Cos (α)
Tatt i betraktning at for verdier av α mellom 0º og 90º, er sinus- og cosinusfunksjonene begge positive, og at kvotienten mellom sinus og cosinus er tangenten, har vi:
Brunbrun (α) ≤ μog
Likheten gjelder for en bestemt verdi av α kalt den kritiske vinkelen og som vi betegner med α *, det vil si:
μog = Brunbrun (α *)
Den kritiske vinkelen bestemmes eksperimentelt, og øker gradvis hellingen til den rette vinkelen der blokken begynner å gli, det vil si den kritiske vinkelen α *.
I boken i figur 1 ble denne vinkelen bestemt eksperimentelt og resulterte i 24 °. Da er koeffisienten for statisk friksjon:
μog = Brunbrun (24º) = 0,45.
Det er et positivt tall mellom 0 og uendelig. Hvis μog = 0 overflatene er helt glatte. Hvis μog → ∞ overflatene er perfekt sammenføyde eller sveisede.
Generelt er verdien av friksjonskoeffisienten mellom 0 og 10.
Trening
I sprint- eller dragsterløp oppnås akselerasjoner på opptil 4g under oppstarten, som oppnås nøyaktig når dekkene ikke glir i forhold til fortauet..
Dette er fordi den statiske friksjonskoeffisienten alltid er større enn den dynamiske friksjonskoeffisienten..
Forutsatt at totalvekten til kjøretøyet pluss sjåføren er 600 kg og at bakhjulene bærer 80% av vekten, bestemmer du kraften til statisk friksjon under 4g-start og koeffisienten for statisk friksjon mellom dekk og fortau..

Løsning
I følge Newtons andre lov er den resulterende kraften lik den totale massen av kjøretøyet ganger akselerasjonen den får.
Ettersom kjøretøyet er i vertikal likevekt, avbrytes det normale og vekten, noe som etterlater å tvinge friksjonskraften F som fortauet utøver på trekkhjulens kontaktområde, slik at:
F = m (4g) = 600 kg (4 x 9,8 m / sto) = 23520 N = 2400 kg-f
Dette betyr at trekkraften er 2,4 tonn.
Friksjonskraften som hjulet utøver på bakken, går bakover, men reaksjonen, som er den samme og motsatte, virker på dekket og går fremover. Det er kraften som driver kjøretøyet.
Selvfølgelig produseres all denne kraften av motoren som prøver å skyve gulvet tilbake gjennom hjulet, men hjulet og gulvet er koblet sammen med friksjonskraft.
For å bestemme koeffisienten for statisk friksjon bruker vi det faktum at den oppnådde F er den maksimale mulige friksjonen, siden vi er på grensen for maksimal akselerasjon, og derfor:
F = μog N = μe (0,8 mg)
Det ble tatt hensyn til at bakhjulene støtter 0,8 ganger vekten. Å løse for friksjonskoeffisienten, får vi:
μog = F / (0,8 mg) = 23520 N / (0,8 x 600 kg x 9,8 m / s ^ 2) = 5.
Konklusjon: μog = 5.
Referanser
- Alonso M., Finn E. 1970. Fysikk bind I: Mekanikk. Inter-American Educational Fund S.A.
- Bauer, W. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
- Hewitt, P. 2012. Konseptuell fysikk. Femte utgave.
- Rex, A. 2011. Fundamentals of Physics. Pearson. 190-200.
- Young, Hugh. 2015. Universitetsfysikk med moderne fysikk. 14. utg. Pearson.


Ingen har kommentert denne artikkelen ennå.