
Sentrifugalkraftformler, hvordan man beregner det, eksempler, øvelser
De sentrifugalkraft det har en tendens til å presse ut svinglegemer rundt en kurve. Det regnes som en fiktiv styrke, pseudoforce eller treghetskraft, fordi det ikke er forårsaket av samspill mellom virkelige objekter, men er en manifestasjon av treghet av kroppene. Treghet er egenskapen som gjør at objekter ønsker å bevare hviletilstanden eller med ensartet rettlinjet bevegelse, hvis de har en..
Begrepet "sentrifugalkraft" ble laget av forskeren Christian Huygens (1629-1695). Han uttalte at den krumlinjære bevegelsen til planetene ville ha en tendens til å bevege dem bort med mindre solen utøvde noe kraft for å holde dem tilbake, og han beregnet at denne kraften var proporsjonal med kvadratet av hastigheten og omvendt proporsjonal med radiusen til den beskrevne omkretsen..

For de som reiser med bil er sentrifugalkraft ikke fiktiv i det hele tatt. Passasjerer i en bil som svinger til høyre føles presset til venstre, og omvendt når bilen svinger til venstre, opplever folk en kraft til høyre, som ser ut til å ville flytte dem bort fra sentrum av kurven..
Størrelsen på sentrifugalkraften Fg beregnes ved hjelp av følgende uttrykk:
-Fg er størrelsen på sentrifugalkraften
-m er massen til objektet
-v er hastigheten
-R er radien til den buede stien.
Kraft er en vektor, derfor brukes fet skrift for å skille den fra størrelsen, som er en skalar.
Du må alltid huske på det Fg vises bare når bevegelse er beskrevet ved hjelp av en akselerert referanseramme.
I eksemplet som ble beskrevet i begynnelsen utgjør den roterende bilen en akselerert referanse, siden den krever sentripetal akselerasjon, så jeg kan snu meg.
Artikkelindeks
- 1 Hvordan beregner du sentrifugalkraften?
- 1.1 Diagram over fritt kropp i et treghets- og ikke-treghetssystem
- 2 Eksempler
- 3 Øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 4 Søknader
- 4.1 Sentrifuger
- 4.2 Skiver
- 4.3 Kan ikke kurver
- 5 Referanser
Hvordan beregner du sentrifugalkraften?
Valget av referansesystem er avgjørende for forståelsen av bevegelsen. En akselerert referanseramme er også kjent som en ikke-treghetsramme..
I denne typen system, som en snurrende bil, dukker opp fiktive krefter som sentrifugalkraft, hvis opprinnelse ikke er et reelt samspill mellom objekter. En passasjer kan ikke si hva som skyver ham ut av kurven, han kan bare bekrefte at dette er tilfelle.
På den annen side, i et treghetsreferansesystem, oppstår samspillet mellom virkelige objekter, for eksempel kroppen i bevegelse og jorden, noe som gir vekt, eller mellom kroppen og overflaten den beveger seg på, som har friksjon og vanlig.
En observatør som står på siden av veien og ser hvordan bilen svinger kurven, er et godt eksempel på et treghetsreferansesystem. For denne observatøren snur bilen seg fordi en kraft rettet mot sentrum av kurven virker på den, som tvinger den til ikke å forlate den. Det handler om sentripetal kraft produsert av friksjon mellom dekk og fortau.
I en treghetsreferanseramme vises ikke sentrifugalkraften. Derfor er det første trinnet for å beregne det å nøye velge referansesystemet som skal brukes til å beskrive bevegelsen..
Til slutt skal det bemerkes at treghetsreferansesystemene ikke nødvendigvis trenger å være i ro, som observatøren som ser på kjøretøyet vri kurven. En treghetsreferanseramme, kjent som laboratorieramme, det kan også være på farta. Selvfølgelig med konstant hastighet med hensyn til en treghet.
Frikroppsdiagram i et treghets- og ikke-treghetssystem
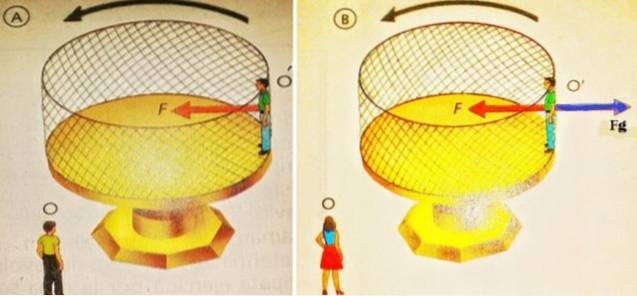
I neste figur til venstre står en observatør O og ser på O ', som er på plattformen som roterer i angitt retning. For O, som er en treghetsramme, fortsetter absolutt O 'å rotere på grunn av sentripetalkraften Fc produsert av veggen på gitteret på baksiden av O '.

Bare i treghetsreferanserammer er det gyldig å anvende Newtons andre lov, som sier at nettokraften er lik masseproduktet og akselerasjonen. Og når vi gjør det, med frikroppsdiagrammet vist, får vi:
Fc = mac
Fc= mvto / R
På samme måte er det i figuren til høyre også et frikroppsdiagram som beskriver hva observatøren O 'ser. Fra sitt synspunkt er han i ro, derfor balanserer kreftene på ham.
Disse kreftene er: de normale F, at veggen utøver på den, i rødt og rettet mot sentrum og sentrifugalkraften Fg som skyver den utover og som ikke kommer fra noen interaksjon, er en ikke-treghetskraft som vises i de roterende referanserammene.
Sentrifugalkraften er fiktiv, den balanseres av en reell kraft, kontakten eller normal kraft som peker mot sentrum. Derfor:
∑Fx = 0 → Fg - F = 0
Fg = F
Eksempler
Selv om sentrifugalkraft betraktes som en pseudokraft, er dens virkninger ganske reelle, som man kan se i følgende eksempler:
- I ethvert spinnende spill i en fornøyelsespark er sentrifugalkraft til stede. Hun sørger for at vi "stikker av fra sentrum" og tilbyr konstant motstand hvis du prøver å gå inn i sentrum av en karusell i bevegelse. I følgende pendel kan du se sentrifugalkraften:
- Coriolis-effekten oppstår fra jordens rotasjon, noe som får jorden til å slutte å være en treghetsramme. Så dukker Coriolis-styrken opp, som er en pseudokraft som avbøyer objekter sideveis, akkurat som folk som prøver å gå på en platespiller..
Opplæring
Øvelse 1
En bil som snurrer med akselerasjon TIL til høyre er et kosedyr hengende fra innsiden av sidespeilet. Tegn og sammenlign frikroppsdiagrammene til leketøyet sett fra:
a) Treghetsreferanserammen til en observatør som står på veien.
b) En passasjer som reiser i bilen.
Løsning til
En observatør som står på veien merker at leketøyet beveger seg raskt, med akselerasjon TIL til høyre.
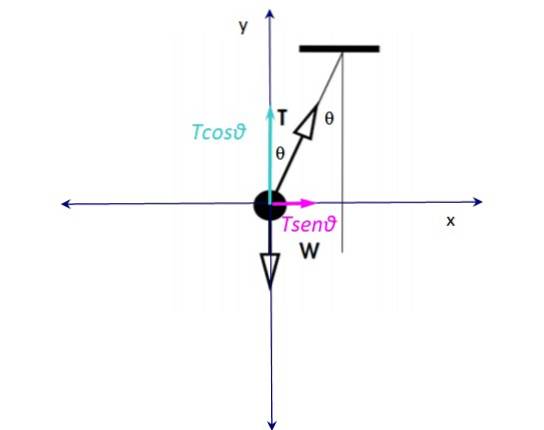
Det er to krefter som virker på leketøyet: på den ene siden spenningen i strengen T og loddrett vekt ned W. Vekten balanseres med den vertikale strekkomponenten Tcosθ, Og dermed:
W - Tcosθ = 0
Den horisontale komponenten av stress: T. senθ er den ubalanserte kraften som er ansvarlig for akselerasjonen til høyre, derfor er sentripetalkraften:
Fc= T. sinθ = mac
Løsning b
For en passasjer i bilen henger leketøyet i likevekt og diagrammet er som følger:

Som i forrige tilfelle kompenseres vekten og den vertikale komponenten av spenningen. Men den horisontale komponenten balanseres av den fiktive kraften Fg = mA, så det:
-mA + Tsenθ = 0
Fg = mA
Øvelse 2
En mynt er på kanten av en gammel vinylplatespiller, hvis radius er 15 cm og roterer med en hastighet på 33 omdreininger / minutt. Finn den minste statiske friksjonskoeffisienten som er nødvendig for at mynten skal holde seg på plass, ved å bruke referanserammen solidaritet med mynten.
Løsning
På figuren er frikroppsdiagrammet for en observatør som beveger seg med mynten. Det normale N at platespilleren anstrenger vertikalt opp, balanseres med vekten W, mens sentrifugalkraften Fg kompenseres av statisk friksjon Fta på.
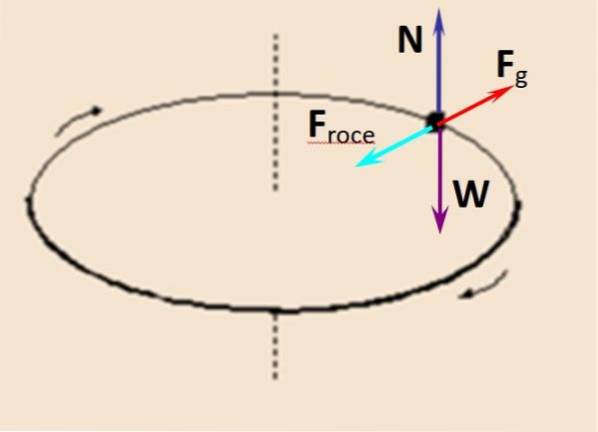
N - W = 0
Fta på - Fg = 0
Størrelsen på sentrifugalkraften er mvto/ R, som sagt i begynnelsen, da:
Fta på = Fg = mvto/ R
På den annen side er den statiske friksjonskraften gitt av:
Fgni = μs.N
Hvor μs er koeffisienten for statisk friksjon, en dimensjonsløs størrelse hvis verdi avhenger av hvordan overflatene er i kontakt. Å erstatte denne ligningen er:
μs.N = mvto/ R → μs = mvto/R.N
Det gjenstår å bestemme størrelsen på det normale, som er relatert til vekten i henhold til N = mg. Bytte ut igjen:
μs = mvto/R.mg → μs = vto/ Rg
Tilbake til uttalelsen rapporterer den at mynten roterer med en hastighet på 33 omdreininger / minutt, som er vinkelhastigheten eller vinkelfrekvensen ω, relatert til lineær hastighet v:
v = ω.R = 33 omdr./min. 2π radianer / turtall 15 cm. (1 min / 60 s) = 51,8 cm / s
μs = vto/Rg=( 51,8 cm / s)to/ (15cm x 981 cm / sto) = 0,18
Resultatene av denne øvelsen ville ha vært de samme hvis en treghetsreferanseramme hadde blitt valgt. I dette tilfellet er den eneste kraften som kan forårsake akselerasjon mot sentrum statisk friksjon..
applikasjoner
Som vi har sagt, er sentrifugalkraften en fiktiv kraft, som ikke vises i treghetsrammer, som er de eneste Newtons lover er gyldige i. I dem er sentripetalkraften ansvarlig for å gi kroppen den nødvendige akselerasjonen mot sentrum.
Sentripetalkraften er ikke en annen kraft fra de som allerede er kjent. Tvert imot, det er nettopp disse som spiller rollen som sentripetale krefter når det passer. For eksempel tyngdekraften som får månen til å bane rundt jorden, spenningen i et tau som en stein roteres med, den statiske friksjonen og den elektrostatiske kraften.
Men siden akselererte referanserammer florerer i praksis, har fiktive krefter veldig reelle effekter. Her er for eksempel tre viktige applikasjoner der de har konkrete effekter:
Sentrifuger
Sentrifuger er instrumenter som er mye brukt i laboratoriet. Ideen er å få en blanding av stoffer til å rotere i høy hastighet, og de stoffene med større masse opplever en større sentrifugalkraft, ifølge ligningen som ble beskrevet i begynnelsen..
Da vil de mest massive partiklene ha en tendens til å bevege seg bort fra rotasjonsaksen, og dermed bli skilt fra de lettere partiklene, som vil forbli nærmere sentrum..
Vaskemaskiner
Automatiske vaskemaskiner har forskjellige sentrifugeringssykluser. I dem sentrifugeres klærne for å eliminere det gjenværende vannet. Jo flere omdreininger syklusen er, desto mindre fuktig blir klærne på slutten av vasken.

Kan ikke kurver
Biler er flinkere til å svinge på veier, fordi sporet skråner litt mot sentrum av kurven, som er kjent som superelevasjon. På denne måten er ikke bilen bare avhengig av den statiske friksjonen mellom dekkene og veien for å fullføre svingen uten å forlate kurven..
Referanser
- Acosta, Victor. Konstruksjon av en didaktisk veiledning om sentrifugalkraft for studenter i syklus V klasse 10. Hentet fra: bdigital.unal.edu.co.
- Toppr. Laws of Motion: Circular Motion. Gjenopprettet fra: toppr.com.
- Resnick, R. (1999). Fysisk. Vol. 1. 3. utgave på spansk. Compañía Editorial Continental S.A. av C.V.
- Autonome universitetet i delstaten Hidalgo. Sentrifugalkraft. Gjenopprettet fra: uaeh.edu.mx
- Wikipedia. Sentrifuger. Gjenopprettet fra: es.wikipedia.org.



Ingen har kommentert denne artikkelen ennå.