
Bijektiv funksjon hva er det, hvordan gjøres det, eksempler, øvelser

EN bijektiv funksjon er en som oppfyller den doble betingelsen om å være injeksjons- og surjektiv. Det vil si at alle elementene i domenet har et enkelt bilde i kodene, og i sin tur er kodene like funksjonens rang ( RF ).
Det oppfylles ved å vurdere et en-til-en-forhold mellom elementene i domenet og kodene. Et enkelt eksempel er funksjonen F: R → R definert av linjen F (x) = x
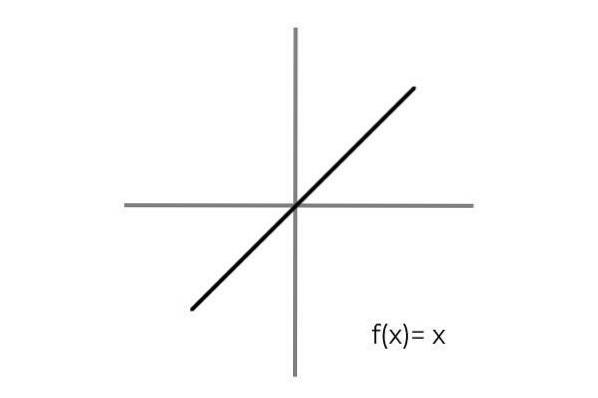
Det observeres at for hver verdi av domenet eller startsettet (begge vilkårene gjelder likt) er det et enkelt bilde i kodesett eller ankomstsett. I tillegg er det ikke noe element i kodene som ikke er et bilde.
Og dermed F: R → R definert av linjen F (x) = x er bijektiv
Artikkelindeks
- 1 Hvordan gjør du en bijektiv funksjon?
- 1.1 Injektivitet av en funksjon
- 1.2 Surjektivitet av en funksjon
- 1.3 Funksjonskondisjonering
- 2 Eksempler: løste øvelser
- 2.1 Øvelse 1
- 2.2 Øvelse 2
- 2.3 Øvelse 3
- 2.4 Øvelse 4
- 3 Foreslåtte øvelser
- 4 Referanser
Hvordan gjør du en bijektiv funksjon?
For å svare på dette er det nødvendig å være tydelig med begrepene det henvises til Injektivitet Y Surjectivity av en funksjon, i tillegg til kriteriene for å kondisjonere funksjoner for å tilpasse dem til kravene.
Injektivitet av en funksjon
En funksjon er injeksjonsmiddel når hvert av elementene i domenet er relatert til et enkelt element i kodene. Et element i kodene kan bare være bildet av et enkelt element i domenet, på denne måten kan ikke verdiene til den avhengige variabelen gjentas.
Å overveie injeksjonsmiddel til en funksjon må følgende oppfylles:
∀ x1 ≠ xto ⇒ F (x1 ) ≠ F (xto )
Surjectivity av en funksjon
En funksjon er klassifisert som surjective, hvis hvert element i kodene er et bilde av minst ett element i domenet.
Å overveie surjective til en funksjon må følgende oppfylles:
Være F: DF → CF
∀ b ℮ CF OG til ℮ DF / F (a) = b
Dette er den algebraiske måten å fastslå at for hver "b" som tilhører CF det er et “a” som tilhører DF slik at funksjonen evaluert i "a" er lik "b".
Funksjonskondisjonering
Noen ganger en funksjon som ikke er det bijective, det kan bli utsatt for visse betingelser. Disse nye forholdene kan gjøre det til et bijektiv funksjon. Alle slags modifikasjoner av domenet og kodene til funksjonen er gyldige, hvor målet er å oppfylle egenskapene til injeksjonsevne og surjektivitet i tilsvarende forhold..
Eksempler: øvelser løst
Øvelse 1
La funksjonen F: R → R definert av linjen F (x) = 5x +1
A: [Alle reelle tall]
Det observeres at for hver verdi av domenet er det et bilde i kodene. Dette bildet er unikt som gjør F være en injeksjonsfunksjon. På samme måte observerer vi at kodene til funksjonen er lik dens rang. Dermed oppfyller betingelsen om surjectivity.
Å være injiserende og surjektiv samtidig kan vi konkludere med at
F: R → R definert av linjen F (x) = 5x +1 er en bijektiv funksjon.
Dette gjelder for alle lineære funksjoner (Funksjoner hvis største grad av variabelen er en).
Øvelse 2
La funksjonen F: R → R definert av F (x) = 3xto - to
Når du tegner en horisontal linje, observeres det at grafen finnes ved mer enn en anledning. På grunn av denne funksjonen F det er ikke injiserende og vil derfor ikke være det bijective så lenge det er definert i R → R
På samme måte er det verdier for kodene som ikke er bilder av noe element i domenet. På grunn av dette er ikke funksjonen surjective, noe som også fortjener å betinges ankomstsettet.
Vi fortsetter med å kondisjonere domenet og kodene til funksjonen
F: [0 , ∞] → [- to , ∞ ]
Der det observeres at det nye domenet omfatter verdiene fra null til positiv uendelig. Unngå repetisjon av verdier som påvirker injeksjonsevnen.
På samme måte har kodemenyen blitt modifisert, teller fra "-2" til positiv uendelig, og eliminert fra kodomenet verdiene som ikke tilsvarte noe element i domenet
På denne måten kan det sikres at F : [0 , ∞] → [- to , ∞ ] definert av F (x) = 3xto - to
Det er bijektiv
Øvelse 3
La funksjonen F: R → R definert av F (x) = Sen (x)
I intervallet [ -∞ , +∞ ] sinusfunksjonen varierer resultatene mellom null og en.
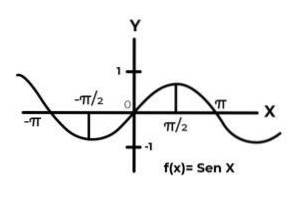
Funksjonen F den tilsvarer ikke kriteriene for injektivitet og surjektivitet, fordi verdiene til den avhengige variabelen gjentas hvert intervall på π. Også vilkårene for kodene utenfor intervallet [-elven] De er ikke et bilde av noe element i domenet.
Når du studerer grafen til funksjonen F (x) = Sen (x) intervaller observeres der at kurvens oppførsel oppfyller kriteriene for bijektivitet. Som for eksempel intervallet DF = [ π / 2,3π / 2 ] for domenet. Y CF = [-1, 1] for kodene.
Hvor funksjonen varierer, blir resultatet fra 1 til -1, uten å gjenta noen verdi i den avhengige variabelen. Og samtidig er kodene like verdiene som er benyttet av uttrykket Sen (x)
På denne måten funksjonen F: [ π / 2,3π / 2 ] → [-1, 1] definert av F (x) = Sen (x). Det er bijektiv
Øvelse 4
Oppgi nødvendige betingelser for DF og CF. Så uttrykket
F (x) = -xto være bijective.
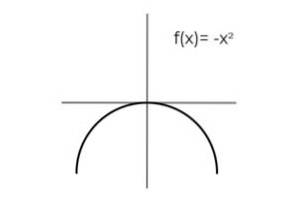
Gjentakelsen av resultatene observeres når variabelen tar motsatte verdier:
F (2) = F (-2) = -4
F (3) = F (-3) = -9
F (4) = F (-4) = -16
Domenet er betinget, og begrenser det til høyre side av den virkelige linjen.
DF = [0 , +∞ ]
På samme måte observeres det at rekkevidden til denne funksjonen er intervallet [ -∞ , 0], som når de fungerer som et kodomain oppfyller vilkårene for surjectivity.
På denne måten kan vi konkludere med det
Uttrykket F: [0 , +∞ ] → [ -∞ , 0] definert av F (x) = -xto Det er bijektiv
Foreslåtte øvelser
Sjekk om følgende funksjoner er relevante:
F: [0 , ∞) → R definert av F (x) = 3 (x + 1)to +to
F: [ 3π / 2,5π / 2 ] → R definert av F (x) = 5ctg (x)
F: [ -π,π ] → R definert av F (x) = Cos (x - 3)
F: R → R definert av linjen F (x) = -5x + 4
Referanser
- Introduksjon til logikk og kritisk tenking. Merrilee H. Laks. University of Pittsburgh
- Problemer i matematisk analyse. Piotr Biler, Alfred Witkowski. Universitetet i Wroclaw. Polen.
- Elementer av abstrakt analyse. Mícheál O'Searcoid PhD. Institutt for matematikk. University college Dublin, Beldfield, Dublind 4
- Introduksjon til logikk og metodikk for deduktive vitenskaper. Alfred Tarski, New York Oxford. Oxford University press.
- Prinsipper for matematisk analyse. Enrique Linés Escardó. Redaksjonell Reverté S. A 1991. Barcelona Spania.

Ingen har kommentert denne artikkelen ennå.