
Injeksjonsfunksjon hva det er, hva det er til og eksempler

EN injeksjonsfunksjon er en hvilken som helst forbindelse mellom elementer av domenet og et enkelt element i kodene. Også kjent som funksjon en etter en ( elleve ), er en del av klassifiseringen av funksjoner med hensyn til måten elementene deres er relatert til.
Et element i kodene kan bare være bildet av et enkelt element i domenet, på denne måten kan ikke verdiene til den avhengige variabelen gjentas.
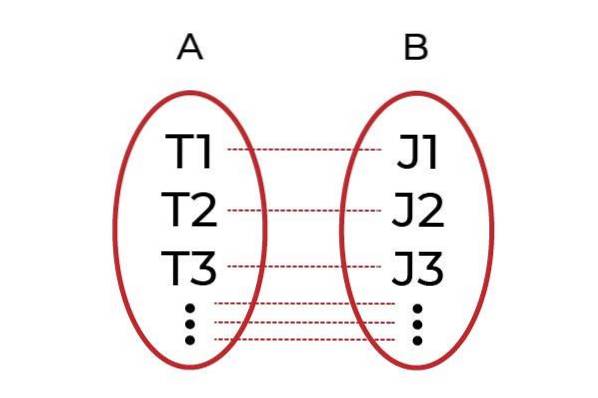
Et klart eksempel ville være å gruppere menn med jobber i gruppe A, og i gruppe B alle sjefer. Funksjonen F Det vil være den som forbinder hver arbeider med sjefen sin. Hvis hver arbeider er assosiert med en annen sjef gjennom F, deretter F vil være en injeksjonsfunksjon.
Å overveie injeksjonsmiddel til en funksjon må følgende oppfylles:
∀ x1 ≠ xto ⇒ F (x1 ) ≠ F (xto )
Dette er den algebraiske måten å si på For alle x1 forskjellig fra xto du har en F (x1 ) forskjellig fra F (xto ).
Artikkelindeks
- 1 Hva er injeksjonsfunksjonene for?
- 1.1 Funksjonskondisjonering
- 2 Eksempler på injeksjonsfunksjoner med løste øvelser
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 2.3 Eksempel 3
- 2.4 Eksempel 4
- 2.5 Eksempel 5
- 2.6 Eksempel 6
- 2.7 Eksempel 7
- 3 Øvelser foreslått for klasse / hjem
- 4 Referanser
Hva er injeksjonsfunksjoner for?
Injektivitet er en egenskap for kontinuerlige funksjoner, siden de sikrer tildelingen av bilder for hvert element i domenet, et viktig aspekt i kontinuiteten til en funksjon..
Når du tegner en linje parallelt med aksen X på grafen til en injeksjonsfunksjon, bør du bare berøre grafen på et enkelt punkt, uavhengig av høyden eller størrelsen på Y linjen er tegnet. Dette er den grafiske måten å teste injeksjonsevnen til en funksjon.
En annen måte å teste om en funksjon er injeksjonsmiddel, er å løse for den uavhengige variabelen X når det gjelder den avhengige variabelen Y. Da må det verifiseres om domenet til dette nye uttrykket inneholder reelle tall, samtidig som for hver verdi av Y det er en enkelt verdi på X.
Funksjonene eller ordenforholdene adlyder blant annet notasjonen F: DF→CF
Hva blir lest F kjører fra DF opp til CF
Hvor funksjonen F relatere settene Domene Y Codomain. Også kjent som startsett og målsett.
Dominion DF inneholder tillatte verdier for den uavhengige variabelen. Kodemannen CF Den består av alle verdiene som er tilgjengelige for den avhengige variabelen. Elementene i CF Relatert til DF er kjent som Funksjonsområde (RF ).
Funksjonskondisjonering
Noen ganger kan en funksjon som ikke er injiserende, bli utsatt for visse forhold. Disse nye forholdene kan gjøre det til et injeksjonsfunksjon. Alle slags modifikasjoner av domenet og kodene til funksjonen er gyldige, der målet er å oppfylle egenskapene til injeksjonsevne i tilsvarende forhold.
Eksempler på injeksjonsfunksjoner med løste øvelser
Eksempel 1
La funksjonen F: R → R definert av linjen F (x) = 2x - 3
A: [Alle reelle tall]
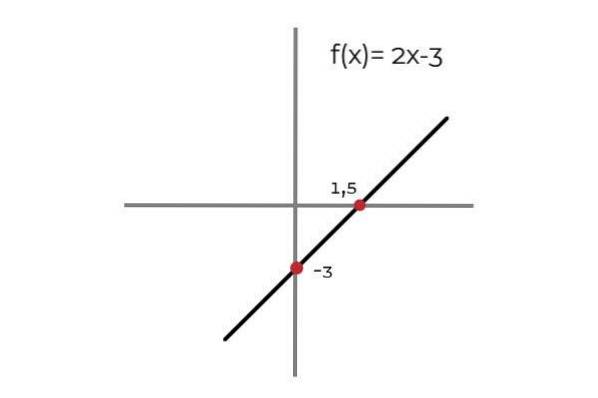
Det observeres at for hver verdi av domenet er det et bilde i kodene. Dette bildet er unikt som gjør F til en injeksjonsfunksjon. Dette gjelder for alle lineære funksjoner (Funksjoner hvis største grad av variabelen er en).
Eksempel 2
La funksjonen F: R → R definert av F (x) = xto +1
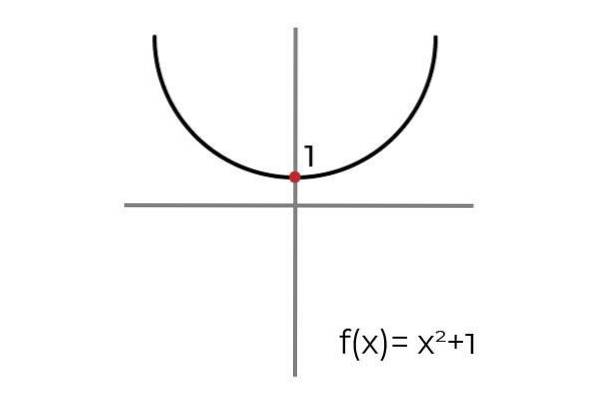
Når du tegner en horisontal linje, observeres det at grafen finnes ved mer enn en anledning. På grunn av denne funksjonen F det er ikke injiserende så lenge det er definert R → R
Vi fortsetter med å konditionere domenet til funksjonen:
F: R+ ELLER 0 → R
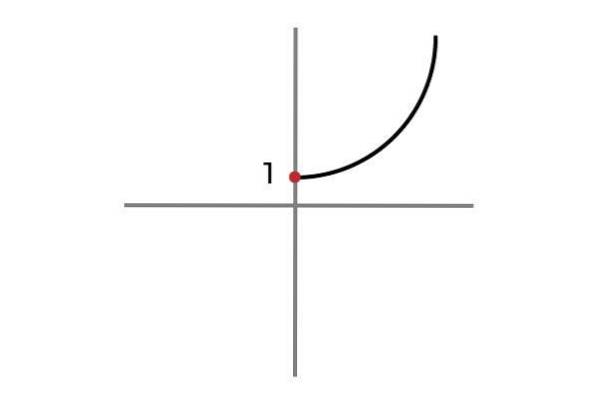
Nå tar den uavhengige variabelen ikke negative verdier, på denne måten unngås gjentatte resultater og funksjonen F: R+ ELLER 0 → R definert av F (x) = xto + 1 er injiserende.
En annen homolog løsning ville være å begrense domenet til venstre, det vil si å begrense funksjonen til å bare ta negative og nullverdier.
Vi fortsetter med å kondisjonere domenet til funksjonen
F: R- ELLER 0 → R
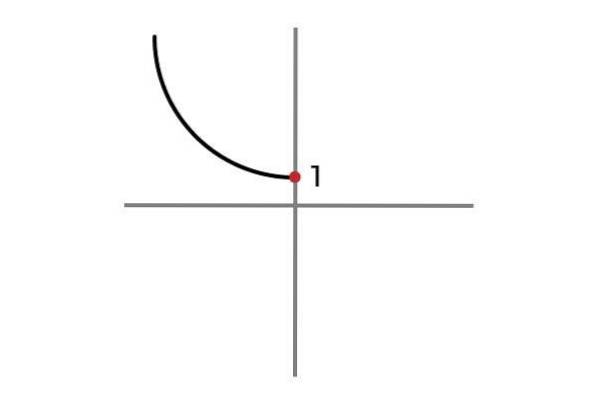
Nå tar den uavhengige variabelen ikke negative verdier, på denne måten unngås gjentatte resultater og funksjonen F: R- ELLER 0 → R definert av F (x) = xto + 1 er injiserende.
Trigonometriske funksjoner har atferd som ligner på bølger, hvor det er veldig vanlig å finne repetisjoner av verdier i den avhengige variabelen. Gjennom spesifikk kondisjonering, basert på forkunnskap om disse funksjonene, kan vi begrense domenet for å oppfylle vilkårene for injeksjonsevne.
Eksempel 3
La funksjonen F: [ -π / 2, π / 2 ] → R definert av F (x) = Cos (x)
I intervallet [ -π / 2 → π / 2 ] cosinusfunksjonen varierer resultatene mellom null og en.
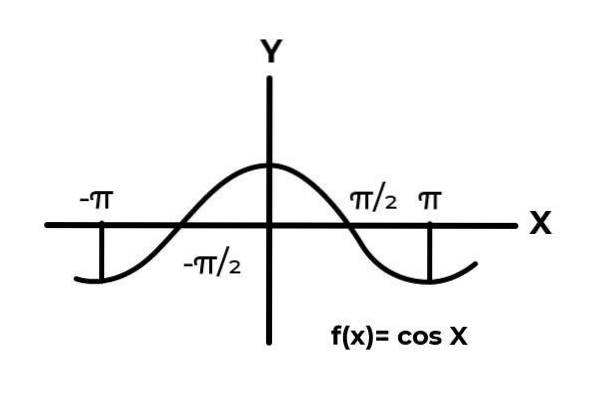
Som det fremgår av grafen. Start fra bunnen av x = -π / 2 når deretter et maksimum på null. Det er etter x = 0 at verdiene begynner å gjenta seg, til de kommer tilbake til null inn x = π / 2. På denne måten er det kjent at F (x) = Cos (x) er ikke injiserende for intervallet [ -π / 2, π / 2 ] .
Når du studerer grafen til funksjonen F (x) = Cos (x) intervaller observeres der kurvens oppførsel tilpasser seg injeksjonskriteriene. Som for eksempel intervallet
[0 , π ]
Hvor funksjonen varierer, blir resultatet fra 1 til -1, uten å gjenta noen verdi i den avhengige variabelen.
På denne måten fungerer funksjonen F: [0 , π ] → R definert av F (x) = Cos (x). Det er injiserende
Det er ikke-lineære funksjoner der lignende tilfeller oppstår. For uttrykk av rasjonell type, der nevneren inneholder minst en variabel, er det begrensninger som forhindrer injeksjonsevnen til forholdet.
Eksempel 4
La funksjonen F: R → R definert av F (x) = 10 / x
Funksjonen er definert for alle reelle tall unntatt 0 som har en ubestemmelighet (kan ikke deles med null).
Når du nærmer deg null fra venstre, tar den avhengige variabelen veldig store negative verdier, og umiddelbart etter null tar verdiene til den avhengige variabelen store positive tall.
Denne forstyrrelsen forårsaker uttrykket F: R → R definert av F (x) = 10 / x
Ikke vær injiserende.
Som sett i de foregående eksemplene tjener utelukkelsen av verdier i domenet til å "reparere" disse ubestemmelsene. Vi fortsetter å ekskludere null fra domenet, og lar avgangs- og ankomstsettene være definert som følger:
R - 0 → R
Hvor R - 0 symboliserer realene bortsett fra et sett hvis eneste element er null.
På denne måten uttrykket F: R - 0 → R definert av F (x) = 10 / x er injeksjonsdyktig.
Eksempel 5
La funksjonen F: [0 , π ] → R definert av F (x) = Sen (x)
I intervallet [0 , π ] sinusfunksjonen varierer resultatene mellom null og en.
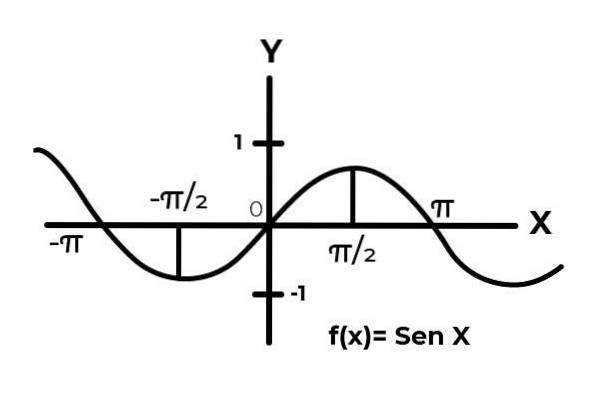
Som det fremgår av grafen. Start fra bunnen av x = 0 og nå et maksimum i x = π / 2. Det er etter x = π / 2 som verdiene begynner å gjenta, til de returnerer til null x = π. På denne måten er det kjent at F (x) = Sen (x) er ikke injiserende for intervallet [0 , π ] .
Når du studerer grafen til funksjonen F (x) = Sen (x) intervaller observeres der kurvens oppførsel tilpasser seg injeksjonskriteriene. Som for eksempel intervallet [ π / 2,3π / 2 ]
Hvor funksjonen varierer, blir resultatet fra 1 til -1, uten å gjenta noen verdi i den avhengige variabelen.
På denne måten funksjonen F: [ π / 2,3π / 2 ] → R definert av F (x) = Sen (x). Det er injiserende
Eksempel 6
Sjekk om funksjonen F: [0, ∞) → R definert av F (x) = 3xto det er injiserende.
Denne gangen er uttrykkets domene allerede begrenset. Det observeres også at verdiene til den avhengige variabelen ikke gjentar seg selv i dette intervallet.
Derfor kan det konkluderes med at F: [0, ∞) → R definert av F (x) = 3xto det er injiserende
Eksempel 7
Identifiser hvilken av de følgende funksjonene
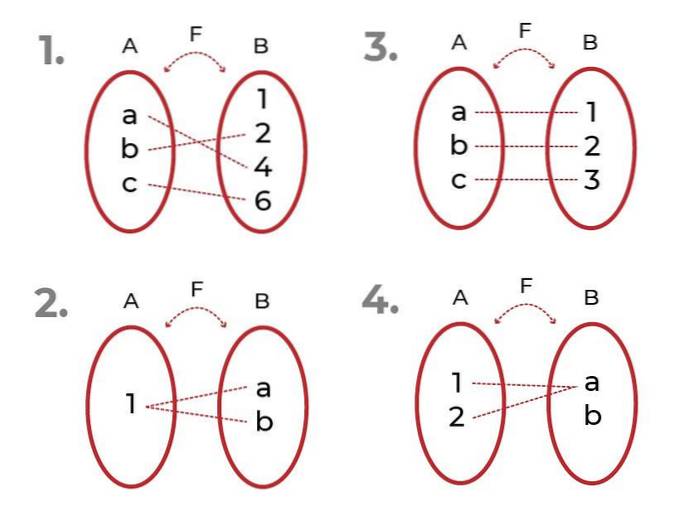
- Det er injiserende. De tilknyttede elementene i kodene er unike for hver verdi av den uavhengige variabelen.
- Det er ikke injiserende. Det er elementer i kodene tilknyttet mer enn ett element i startsettet.
- Det er injiserende
- Det er ikke injiserende
Foreslåtte øvelser for klasse / hjem
Sjekk om følgende funksjoner er injiserende:
F: [0, ∞) → R definert av F (x) = (x + 3)to
F: [ π / 2,3π / 2 ] → R definert av F (x) = Tan (x)
F: [ -π,π ] → R definert av F (x) = Cos (x + 1)
F: R → R definert av linjen F (x) = 7x + 2
Referanser
- Introduksjon til logikk og kritisk tenking. Merrilee H. Laks. University of Pittsburgh
- Problemer i matematisk analyse. Piotr Biler, Alfred Witkowski. Universitetet i Wroclaw. Polen.
- Elementer av abstrakt analyse. Mícheál O'Searcoid PhD. Institutt for matematikk. University college Dublin, Beldfield, Dublind 4.
- Introduksjon til logikk og metodikk for deduktive vitenskaper. Alfred Tarski, New York Oxford. Oxford University press.
- Prinsipper for matematisk analyse. Enrique Linés Escardó. Redaksjonell Reverté S. A 1991. Barcelona Spania.


Ingen har kommentert denne artikkelen ennå.