
Grunnleggende trigonometriske funksjoner, i det kartesiske planet, eksempler, trening
De trigonometriske funksjoner av ekte variabel tilsvarer hvilken som helst vinkel (uttrykt i radianer), et trigonometrisk forhold, som kan være sinus, cosinus, tangens, cotangens, secant og cosecant.
På denne måten har vi de seks trigonometriske funksjonene: sinus, cosinus, tangens, cosecant, secant og cotangent..
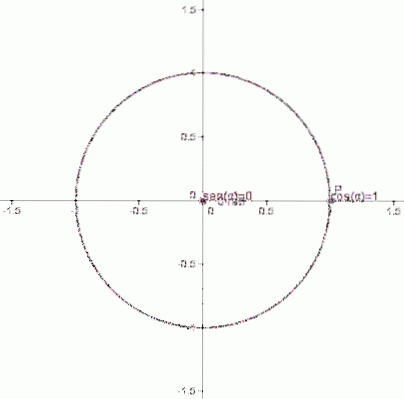
De trigonometriske funksjonene for vinkler mellom 0 og 2π er definert ved hjelp av enhetssirkelen, med radius 1 og hvis senter sammenfaller med opprinnelsen til det kartesiske koordinatsystemet: punktet (0,0).
Vi kan finne hvilket som helst punkt P med koordinater (x, y) på denne omkretsen.
Segmentet som forbinder opprinnelsen med P, sammen med de respektive segmentene som forbinder projeksjonene av P på koordinataksene, utgjør en høyre trekant, hvis trigonometriske forhold er kjent som forholdet mellom sidene av trekanten. A) Ja:
- sin θ = motsatt ben / hypotenus
- cos θ = tilstøtende ben / hypotenus
- tg θ = motsatt ben / tilstøtende ben
Og nå er årsakene som er omvendt av de forrige:
- sek θ = hypotenus / tilstøtende ben
- cosec θ = hypotenus / motsatt ben
- ctg θ = tilstøtende ben / motsatt ben
I enhetssirkelen er hypotenusen til en hvilken som helst trekant lik 1 og bena er verdt x og y, så:
synd θ = y
cos θ = x
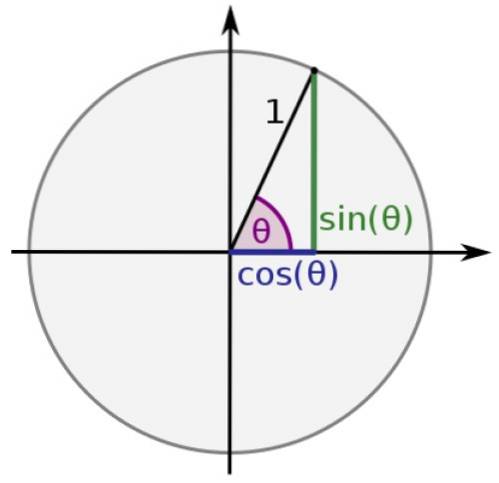
På denne måten får sinus- og cosinusfunksjonene alltid verdier mellom -1 og 1, mens resten:
tg θ = y / x
cosec θ = 1 / y
sek θ = 1 / x
De er ikke definert når x eller Y verdt 0.
Artikkelindeks
- 1 Trigonometriske funksjoner i det kartesiske planet
- 1.1 Funksjon f (x) = sin x
- 1.2 Funksjon f (x) = cos x
- 1.3 Diskontinuerlige trigonometriske funksjoner
- 2 Øvelsen løst
- 2.1 Løsning
- 3 Referanser
Trigonometriske funksjoner på det kartesiske planet
Som vi vil se nedenfor, er trigonometriske funksjoner preget av å være periodiske. Derfor er de ikke bindende, bortsett fra i et begrenset domene..
Funksjon f (x) = sin x
Fra den trigonometriske sirkelen ved punkt P (1,0) er vinkelen 0 radianer. Deretter roterer radius mot klokken, og sin x-funksjonen vokser gradvis til den når π / 2 radianer (90º), tilsvarende omtrent 1 571 radianer..
Der når den verdien y = 1 og avtar til den når null i π radianer (180 °). Senere synker den enda mer, siden verdien blir negativ til den når -1 når vinkelen er 3π / 2 radianer (270 °).
Til slutt øker den igjen til den kommer tilbake til null i 360 °, hvor alt begynner igjen. Dette gjør at y = sin x a periodisk funksjon av periode 2π, derfor er ikke sinusfunksjonen biniv.
Grafen er også symmetrisk med hensyn til punktet (0,0), derfor er funksjonen merkelig.
Deretter grafen til y = sin x:
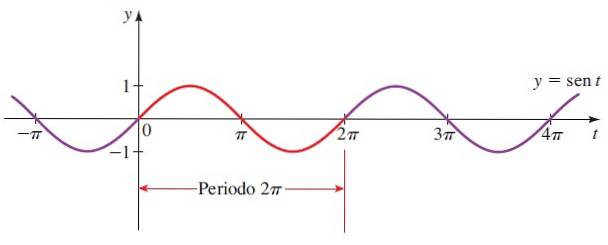
Seksjonen i rødt er den første perioden. Negative vinkler blir også vurdert, siden radiusen til den trigonometriske sirkelen kan rotere med klokken.
Sin domene x = Alle virkelige.
Sinens rekkevidde eller sti x = [-1,1]
Funksjon f (x) = cos x
På punktet P (1,0) er cosinusfunksjonen verdt 1 og derfra avtar den og når 0 når vinkelen er π / 2. Den fortsetter å synke og tar negative verdier, til den når -1 i vinkelen π.
Så begynner den gradvis å øke til den når 0 i 3π / 2 og går tilbake til verdien 1 når radiusen har gjort en fullstendig omdreining. Derfra gjentas syklusen, siden cos x er periodisk og også er jevn (symmetrisk rundt den vertikale aksen).
Formen på cosinusfunksjonen er den samme som sinusfunksjonen, bortsett fra at de forskyves π / 2 i forhold til hverandre..
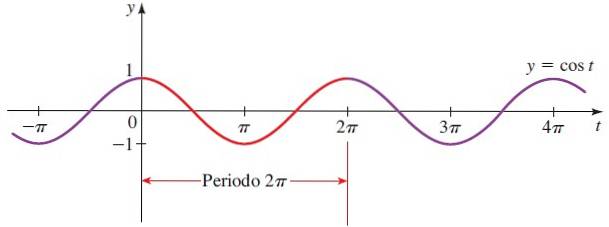
Domain of cos x = Alle virkelige.
Cos x rekkevidde eller reise = [-1,1]
Diskontinuerlige trigonometriske funksjoner
Funksjonene tg x, ctg x, sec x og cosec x er diskontinuerlige, siden de er kvotienter mellom sinus og cosinus, eller omvendt. Siden disse er verdt 0 i noen vinkler, gjør de funksjonen diskontinuerlig når de vises i nevneren.
Og siden sinus og cosinus er periodiske funksjoner, er funksjonene tg x, ctg x, sec x, cosec x også periodiske..
Tangentfunksjon f (x) = tg x
For tangensfunksjonen er diskontinuitetsverdiene: ± π / 2, ± 3π / 2, ± 5π / 2… Der tar funksjonen veldig store eller veldig små verdier. Generelt skjer dette for alle multipler av π av formen (2n + 1) π / 2, både positive og negative, med n = 0, 1, 2 ...
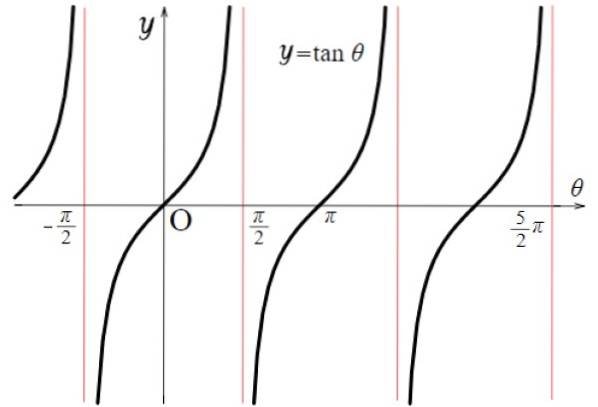
Derfor:
Tg x domene: D = x ∈ R / x ≠ (2n + 1) π / 2; n ∈ Z
Tg x rekkevidde eller reise: Helt ekte.
Merk at funksjonen f (x) = tg x gjentar mellom - π / 2 og + π / 2, derfor er perioden π. I tillegg er det symmetrisk med tanke på opprinnelsen.
Kotangensfunksjon f (x) = ctg x
For denne funksjonen forekommer diskontinuitetsverdiene ved 0, ± π, ± 2π…, det vil si heltallsmultiplene av π.
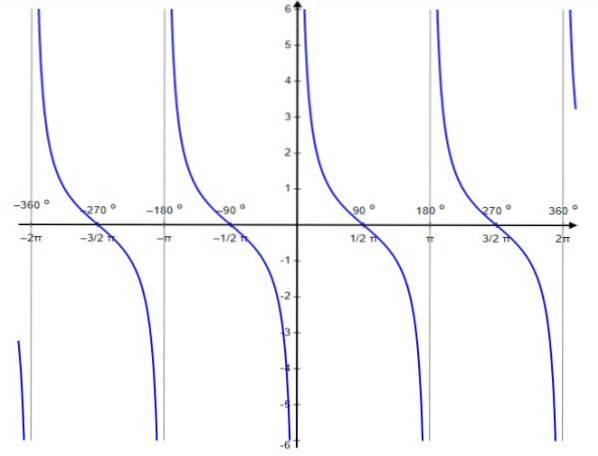
I likhet med tangensfunksjonen, er cotangensfunksjonen periodisk av perioden π. For henne er det sant at:
Ctg x domene: D = x ∈ R / x ≠ n π; n ∈ Z
Ctg x rekkevidde eller reise: Helt ekte.
Sekantfunksjon f (x) = sek x
Sec x-funksjonen har diskontinuitetspoeng ved ± π / 2, ± 3π / 2, ± 5π / 2…, hvor cos x = 0. Det er også periodisk med periode π og det observeres også fra grafen at funksjonen aldri tar verdier i intervallet (-1,1)
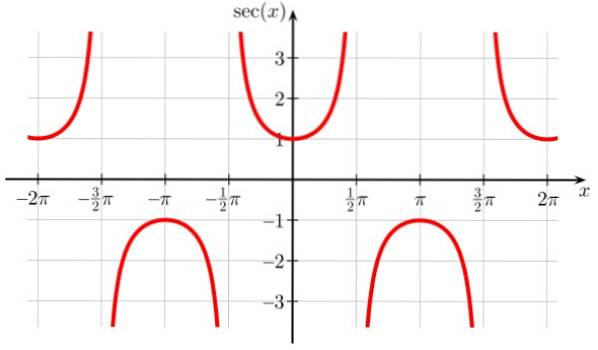
Domenet til sek x: D = x ∈ R / x ≠ (2n + 1) π / 2; n ∈ Z
Sek x rekkevidde eller reise: Alle realer unntatt (-1,1)
Cosecant-funksjon f (x) = cosec x
Det ligner på sekantfunksjonen, selv om den er forskjøvet til høyre, derfor er punktene for diskontinuitet 0, ± π, ± 2π og alle heltallmultipler av π. Det er også periodisk.
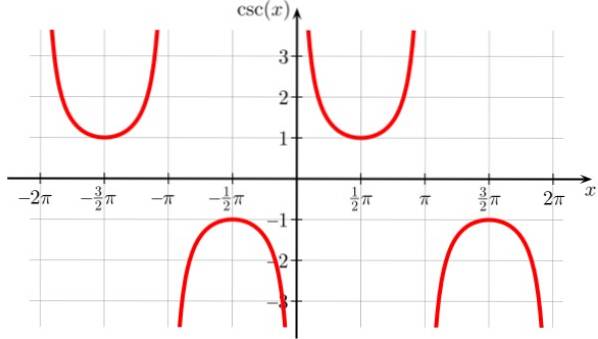
Cosec Domain X: D = x ∈ R / x ≠ n π; n ∈ Z
Høstområde eller sti x: Alle realer unntatt (-1,1)
Treningen løst
En 6 fot høy mann kaster en skygge S hvis lengde er gitt av:
S (t) = 6 │ barneseng (π.t / 12) │
Med S i føtter og t antall timer siden 06:00. Hvor høy er skyggen klokka 8.00, 12.00, 14.00 og 17.45?
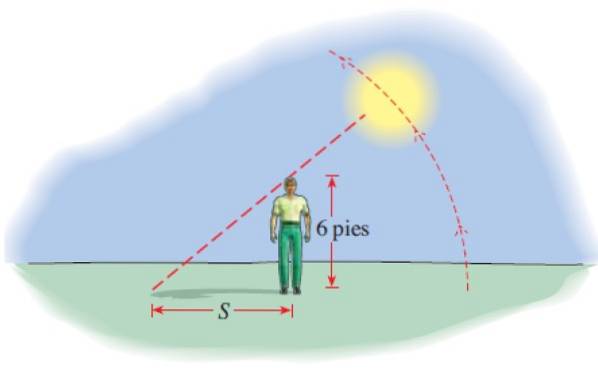
Løsning
Vi må evaluere funksjonen for hver av de gitte verdiene, og merke oss at den må ta den absolutte verdien, siden lengden på skyggen er positiv:
-Klokka 08.00 har det gått 2 timer fra klokken 06.00, derfor er t = 2 og S (t):
S (2) = 6 │ barneseng (π.2 / 12) │ft = 6 │ barneseng (π / 6) │ft = 10,39 fot.
-Når det er 12 N, har t = 6 timer gått, derfor:
S (6) = 6 │cot (π.6 / 12) │ft = 6 │cot (π / 2) │ft = 0 fot. (På den tiden faller solen vertikalt på personens hode).
-Klokka 14 t = 8 timer gått:
S (8) = 6 │ barneseng (π.8 / 12) │ft = 6 │ barneseng (2π / 3) │ft = 3,46 fot.
-Når klokken er 17.45, har det allerede gått 11,75 timer siden klokka 6, så:
S (11,75) = 6 │ barneseng (π x 11,75 / 12) │ føtter = 91,54 fot. På denne timen blir skyggene lengre.
Kan leseren beregne tiden når personens skygge tilsvarer hans høyde??
Referanser
- Carena, M. 2019. Pre-University Mathematics Manual. National University of the Litoral.
- Figuera, J. 1999. Matematikk. Første. Diversifisert. Bolivarian Collegiate Editions.
- Hoffman, J. Selection of Mathematics Topics. Volum 4.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Zill, D. 1984. Algebra og trigonometri. Mcgraw hill.

Ingen har kommentert denne artikkelen ennå.