
Hypercube definisjon, dimensjoner, koordinater, utfoldet
EN hyperkube er en kube av dimensjon n. Det spesielle tilfellet med den firedimensjonale hyperkuben kalles tesseract. En hyperkube eller n-kube består av rette segmenter, alle av samme lengde som er ortogonale ved sine hjørner.
Mennesker oppfatter tredimensjonalt rom: bredde, høyde og dybde, men det er ikke mulig for oss å visualisere en hyperkube med en dimensjon større enn 3.
På det meste kan vi lage projeksjoner av det i et tredimensjonalt rom for å representere det, på en lignende måte som hvordan vi projiserer en kube på et plan for å representere den..
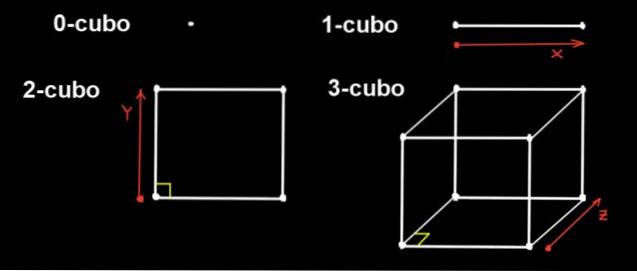
I dimensjon 0 er den eneste figuren punktet, så en 0-kube er et punkt. En 1-kube er et rett segment, som dannes ved å flytte et punkt i en retning en avstand a.
På sin side er en 2-kube en firkant. Den er konstruert ved å forskyve 1-kuben (lengdesegmentet a) i y-retningen, som er ortogonal mot x-retningen, en avstand a.
3-kuben er den vanlige kuben. Den er bygget fra firkanten ved å bevege den i tredje retning (z), som er ortogonal i retning x og y, en avstand til.
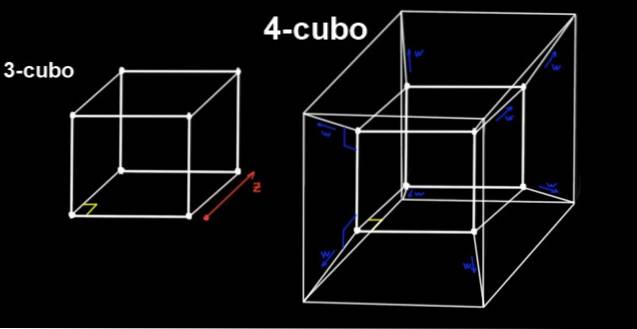
4-kuben er tesserakt, som er bygget fra en 3-kube som forskyver den ortogonalt, en avstand til, mot en fjerde dimensjon (eller fjerde retning), som vi ikke kan oppfatte.
En tesserakt har alle sine rette vinkler, den har 16 hjørner, og alle kantene (18 totalt) har samme lengde til.
Hvis lengden på kantene til en n-kube eller hyperkube av dimensjon n er 1, er det en enhetshyperkube, der den lengste diagonalen måler √n.

Artikkelindeks
- 1 Hva er dimensjoner??
- 1.1 Det tredimensjonale rommet
- 2 Koordinatene til en hyperkube
- 2.1 Brette ut en hyperkube
- 3 Referanser
Hva er dimensjoner??
Dimensjoner er frihetsgraden, eller de mulige retningene et objekt kan bevege seg i.
I dimensjon 0 er det ingen mulighet for å oversette, og det eneste mulige geometriske objektet er poenget.
En dimensjon i det euklidiske rommet representeres av en orientert linje eller akse som definerer den dimensjonen, kalt X-aksen. Skillet mellom to punkter A og B er den euklidiske avstanden:
d = √ [(xtil - xb)to].
I to dimensjoner er rommet representert med to linjer som er ortogonale mot hverandre, kalt X-aksen og Y-aksen..
Posisjonen til et hvilket som helst punkt i dette todimensjonale rommet er gitt av paret av kartesiske koordinater (x, y), og avstanden mellom to punkter A og B vil være:
d = √ [(xtil - xb)to + (Ytil - Yb)to]
Fordi det er et rom der Euklids geometri blir oppfylt.
Tredimensjonalt rom
Tredimensjonalt rom er rommet vi beveger oss i. Den har tre retninger: bredde, høyde og dybde.
I et tomt rom gir hjørnene vinkelrett på hverandre disse tre retningene, og til hver enkelt kan vi knytte en akse: X, Y, Z.
Dette rommet er også euklidisk, og avstanden mellom to punkter A og B beregnes som følger:
d = √ [(xtil - xb)to + (Ytil - Yb)to + (ztil - zb)to]
Mennesker kan ikke oppfatte mer enn tre romlige (eller euklidiske) dimensjoner.
Fra et strengt matematisk synspunkt er det imidlertid mulig å definere et n-dimensjonalt euklidisk rom.
I dette rommet har et punkt koordinater: (x1, x2, x3,…, xn) og avstanden mellom to punkter er:
d = √ [(xFørste - x1 B)to + (x2. plass - x2b)to +… + (Xna - xnb)to].
Den fjerde dimensjonen og tiden
Faktisk behandles tiden i relativitetsteorien som en dimensjon til og en koordinat er knyttet til den.
Men det må avklares at denne koordinaten assosiert med tid er et tenkt tall. Separasjonen av to punkter eller hendelser i romtid er ikke euklidisk, men følger heller Lorentz-beregningen.
En firedimensjonal hyperkube (tesseract) lever ikke i romtid, den tilhører et firedimensjonalt euklidisk hyperrom.

Koordinatene til en hyperkube
Koordinatene til toppunktene til en n-kube sentrert ved opprinnelsen oppnås ved å gjøre alle mulige permutasjoner av følgende uttrykk:
(a / 2) (± 1, ± 1, ± 1,…., ± 1)
Hvor a er lengden på kanten.
-De volum av en n-kube av kant a er: (a / 2)n (ton) = an.
-De lengste diagonal er avstanden mellom motsatte hjørner.
-Følgende er motsatte hjørner i en firkant: (-1, -1) og (+1, +1).
-Og i en Kube: (-1, -1, -1) og (+1, +1, +1).
-De lengste diagonal av en n-kube måler:
d = √ [1 - (- 1))to +… + (1 - (- 1))to] = √ [n 2to] = 2√n
I dette tilfellet ble siden antatt å være a = 2. For en n-kube fra hvilken som helst side vil følgende forbli:
d = a√n.
-En tesserakt har hver av sine 16 hjørner knyttet til fire kanter. Den følgende figuren viser hvordan hjørner er koblet sammen i en tallerkenakt.
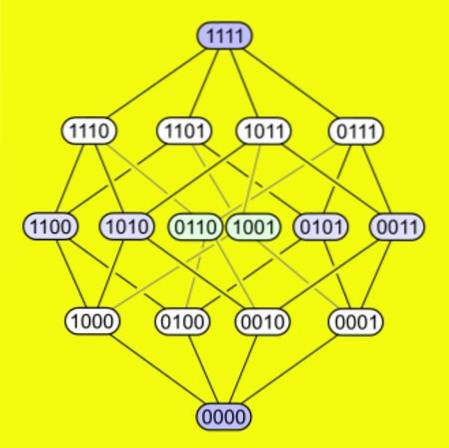
Bretting av en hyperkube
En vanlig geometrisk figur, for eksempel en polyhedron, kan brettes ut til flere figurer med mindre dimensjonalitet.
Når det gjelder en 2-kube (en firkant), kan den brettes ut i fire segmenter, det vil si fire 1-kuber.
Tilsvarende kan en 3-kube brettes ut i seks 2-kuber.

En 4-kube (tesseract) kan brettes ut til åtte 3-kuber.
Følgende animasjon viser utfoldelsen av en teaterakt.
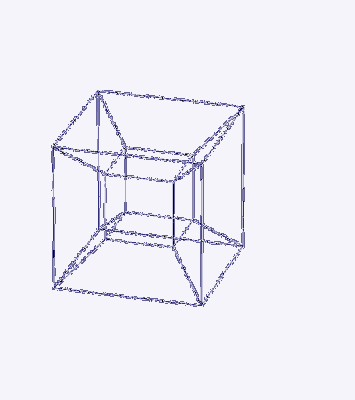

Referanser
- Vitenskapelig kultur. Hypercube, visualiserer den fjerde dimensjonen. Gjenopprettet fra: culturacientifica.com
- Epsilons. Fire-dimensjonal hyperkube eller tesserakt. Gjenopprettet fra: epsilones.com
- Perez R, Aguilera A. En metode for å oppnå en tesserakt fra utviklingen av en hyperkube (4D). Gjenopprettet fra: researchgate.net
- Wikibooks. Matematikk, polyeder, hyperkubber. Gjenopprettet fra: es.wikibooks.org
- Wikipedia. Hypercube. Gjenopprettet fra: en.wikipedia.com
- Wikipedia. Tesseract. Gjenopprettet fra: en.wikipedia.com


Ingen har kommentert denne artikkelen ennå.