
Pythagoras identitetsdemonstrasjon, eksempel, øvelser
De er Pythagoras identiteter alle trigonometriske ligninger som holder for en hvilken som helst verdi av vinkelen og er basert på Pythagoras teorem. Den mest kjente av de pythagoreiske identitetene er den grunnleggende trigonometriske identiteten:
Sento(α) + Costo(α) = 1
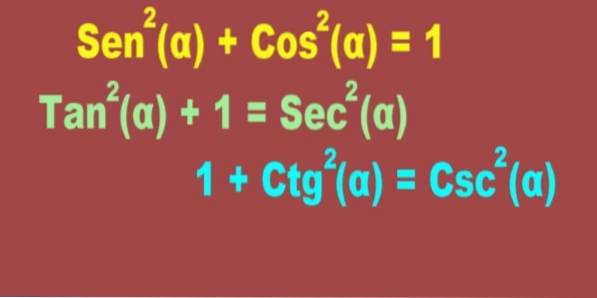
Neste i betydning, og jeg bruker den pythagoreiske identiteten til tangenten og sekanten:
Såto(α) + 1 = Sekto(α)
Og den Pythagoras trigonometriske identiteten som involverer cotangenten og cosecanten:
1 + Ctgto(α) = Cscto(α)
Artikkelindeks
- 1 Demo
- 1.1 Sinus og cosinus
- 1.2 Den grunnleggende identiteten
- 1.3 Tangensaksen
- 1.4 Tangensens pythagoriske identitet
- 2 Eksempel
- 3 Løst øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 4 Referanser
Demonstrasjon
De trigonometriske forholdene bryst Y cosinus de er representert i en sirkel med radius en (1) kjent som en trigonometrisk sirkel. Nevnte sirkel har senter ved opprinnelsen til koordinatene O.
Vinklene måles fra den positive halvaksen til X, for eksempel vinkelen α i figur 2 (se nedenfor). Mot klokken hvis vinkelen er positiv, og med klokken hvis den er en negativ vinkel.
Strålen med opprinnelse O og vinkel α tegnes, som avskjærer enhetssirkelen ved punkt P. Punkt P projiseres ortogonalt på den horisontale aksen X og gir opphav til punkt C. Tilsvarende projiseres P vinkelrett på den vertikale aksen Y og gir plass til punkt S.
Vi har riktig trekant OCP ved C.
Sinus og cosinus
Det skal huskes at det trigonometriske forholdet bryst er definert i en høyre trekant som følger:
Sinusen til en vinkel på trekanten er forholdet eller kvotienten mellom benet motsatt vinkelen og hypotenusen til trekanten.
Anvendt på trekanten OCP i figur 2 vil det se slik ut:
Sen (α) = CP / OP
men CP = OS og OP = 1, slik at:
Sen (α) = OS
Dette betyr at projeksjons-OS på Y-aksen har en verdi lik sinusen til den viste vinkelen. Det skal bemerkes at den maksimale verdien av sinusen til en vinkel (+1) oppstår når α = 90º og minimum (-1) når α = -90º eller α = 270º.
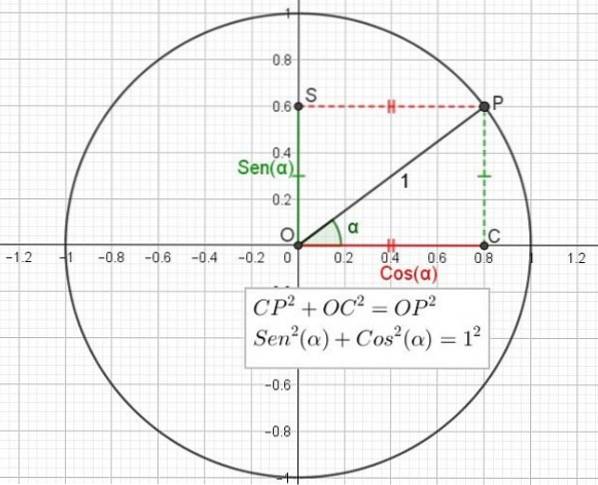
Tilsvarende er cosinusen til en vinkel kvotienten mellom benet ved siden av vinkelen og trekantenes hypotenus..
Anvendt på trekanten OCP i figur 2 vil det se slik ut:
Cos (α) = OC / OP
men OP = 1, slik at:
Cos (α) = OC
Dette betyr at projeksjonen OC på X-aksen har en verdi lik sinusen til den viste vinkelen. Det skal bemerkes at den maksimale verdien av cosinus (+1) oppstår når α = 0º eller α = 360º, mens minimumsverdien for cosinus er (-1) når α = 180º.
Den grunnleggende identiteten
For den rette trekanten OCP i C, brukes den pytagoreiske teoremet, som sier at summen av kvadratet på bena er lik kvadratet til hypotenusen:
CPto + OCto = OPto
Men det er allerede sagt at CP = OS = Sen (α), at OC = Cos (α) og at OP = 1, slik at det forrige uttrykket kan skrives om som en funksjon av sinus og cosinus i vinkelen:
Sento(α) + Costo(α) = 1
Tangensens akse
Akkurat som X-aksen i den trigonometriske sirkelen er cosinusaksen og Y-aksen sinusaksen, er det på samme måte tangensaksen (se figur 3) som nettopp er tangentlinjen til enhetssirkelen ved punktet B av koordinater (1, 0).
Hvis du vil vite verdien av tangenten til en vinkel, tegner du vinkelen fra den positive halvaksen til X, skjæringspunktet mellom vinkelen og tangensens akse definerer et punkt Q, lengden på segmentet OQ er vinkelens tangens.
Dette er per definisjon at tangensen til vinkelen α er det motsatte benet QB mellom det tilstøtende beinet OB. Det vil si at Tan (α) = QB / OB = QB / 1 = QB.
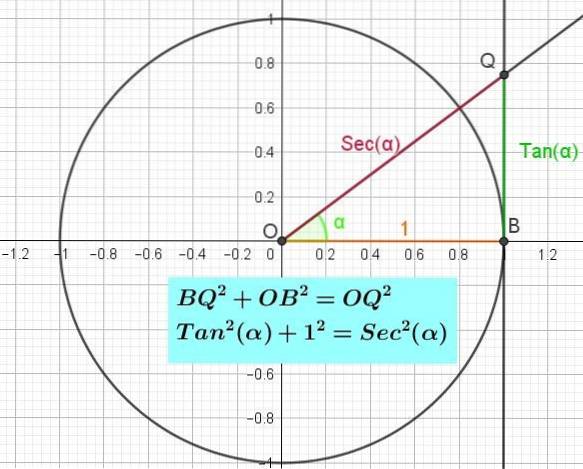
Pythagoras identitet av tangenten
Pythagoras-identiteten til tangenten kan bevises ved å vurdere den rette trekanten OBQ ved B (figur 3). Ved å bruke Pythagoras teorem på denne trekanten har vi den BQto + OBto = OQto. Men det er allerede sagt at BQ = Tan (α), at OB = 1 og at OQ = Sec (α), slik at vi i Pythagoras-likhet erstatter den rette trekanten OBQ vi har:
Såto(α) + 1 = Sekto(α).
Eksempel
Sjekk om de pythagoreiske identitetene er oppfylt i høyre trekant med ben AB = 4 og BC = 3.
Løsning: Bena er kjent, hypotenusen må bestemmes, som er:
AC = √ (AB ^ 2 + BC ^ 2) = √ (4 ^ 2 + 3 ^ 2) = √ (16 + 9) = √ (25) = 5.
Vinkelen ∡BAC vil bli kalt α, ∡BAC = α. Nå bestemmes trigonometriske forhold:
Sen α = BC / AC = 3/5
Cos α = AB / AC = 4/5
Så α = BC / AB = 3/4
Cotan α = AB / BC = 4/3
Sek α = AC / AB = 5/4
Csc α = AC / BC = 5/3
Det begynner med den grunnleggende trigonometriske identiteten:
Sento(α) + Costo(α) = 1
(3/5) ^ 2 + (4/5) ^ 2 = 9/25 + 16/25 = (9 +16) / 25 = 25/25 = 1
Det konkluderes med at det er oppfylt.
- Den neste pythagoreiske identiteten er tangenten:
Såto(α) + 1 = Sekto(α)
(3/4) ^ 2 + 1 = 9/16 + 16/16 = (9 + 16) / 16 = 25/16 = (5/4) ^ 2
Og det konkluderes med at identiteten til tangenten er bekreftet.
- På samme måte som cotangenten:
1 + Ctgto(α) = Cscto(α)
1+ (4/3) ^ 2 = 1 + 16/9 = 25/9 = (5/3) ^ 2
Det konkluderes med at den også er oppfylt, med hvilken oppgaven med å verifisere de pytagoreiske identitetene for den gitte trekanten er fullført..
Løst øvelser
Bevis følgende identiteter, basert på definisjonene av trigonometriske forhold og Pythagoras identiteter.
Øvelse 1
Bevis at Costo x = (1 + Sen x) (1 - Sen x).
Løsning: På høyre side gjenkjennes det bemerkelsesverdige produktet av multiplikasjonen av et binomium med konjugatet, som som kjent er en forskjell i kvadrater:
Costo x = 1to - Sento x
Så passerer begrepet med sinus på høyre side til venstre side med tegnet endret:
Costo x + Sento x = 1
Legg merke til at den grunnleggende trigonometriske identiteten er nådd, så det konkluderes med at det gitte uttrykket er en identitet, det vil si at det er sant for enhver verdi av x.
Øvelse 2
Begynn fra den grunnleggende trigonometriske identiteten og bruk definisjonene av de trigonometriske forholdene, demonstrer den pythagoreiske identiteten til cosecanten.
Løsning: Den grunnleggende identiteten er:
Sento(x) + Costo(x) = 1
Begge medlemmer er delt mellom Sento(x) og nevneren fordeles på det første medlemmet:
Sento(x) / Sento(x) + Costo(x) / Sento(x) = 1 / Sento(x)
Det er forenklet:
1 + (Cos (x) / Sen (x)) ^ 2 = (1 / Sen (x)) ^ 2
Cos (x) / Sen (x) = Cotan (x) er en (ikke-Pythagoras) identitet som bekreftes av definisjonen av trigonometriske forhold. Det samme skjer med følgende identitet: 1 / Sen (x) = Csc (x).
Til slutt må du:
1 + Ctgto(x) = Cscto(x)
Referanser
- Baldor J. (1973). Plan- og romgeometri med innføring i trigonometri. Mellomamerikansk kultur. AC.
- C. E. A. (2003). Element av geometri: med øvelser og geometri av kompasset. University of Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematikk 2. Grupo Editorial Patria.
- IGER. (s.f.). Matematikk Første semester Tacaná. IGER.
- Jr. geometri. (2014). Polygoner. Lulu Press, Inc..
- Miller, Heeren & Hornsby. (2006). Mathematics: Reasoning And Applications (Tiende utgave). Pearson Education.
- Patiño, M. (2006). Matematikk 5. Redaksjonell Progreso.
- Wikipedia. Trigonometri identiteter og formler. Gjenopprettet fra: es.wikipedia.com


Ingen har kommentert denne artikkelen ennå.