De Fermatgrense er en numerisk metode som brukes for å få verdien av hellingen til en linje, som er tangent til en funksjon på et gitt punkt i domenet. Den brukes også til å oppnå kritiske punkter i en funksjon. Uttrykket er definert som:
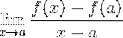
Det er åpenbart at Fermat ikke kjente grunnleggende til avledning, men det var hans studier som fikk en gruppe matematikere til å spørre om tangentlinjer og deres anvendelse i kalkulator..
Artikkelindeks
Den består av en tilnærming på to punkter, som i tidligere forhold danner en sekant linje til funksjonen med skjæringspunkt i par verdier.
Ved å nærme seg variabelen til verdien "a", blir poengparet tvunget til å møte. På denne måten blir den tidligere sekantlinjen tangent til punktet (a; f (a)).
Verdien av kvotienten (x - a), når den blir evaluert i punkt "a", gir en ubestemmelighet av K-type grenser mellom null (K / 0). Hvor disse ubestemmelsene kan brytes gjennom forskjellige faktoriseringsteknikker.
De mest brukte driftsteknikkene er:
-Forskjell på firkanter (ato - bto ) = (a + b) (a - b); Eksistensen av elementet (a-b) innebærer i de fleste tilfeller faktoren som forenkler uttrykket (x-a) i kvotienten til Fermat-grensen.
- Fullføring av firkanter (axto + bx); Etter å ha fullført kvadrater oppnås et Newton binomium, der en av dens to faktorer er forenklet med uttrykket (x - a), og bryter ubestemmelsen.
- Konjugat (a + b) / (a + b); Å multiplisere og dele uttrykket med konjugatet av en eller annen faktor kan være til stor hjelp for å bryte ubestemmelsen.
- Fellesfaktor; I mange tilfeller skjuler resultatet av å betjene telleren for Fermat-grensen f (x) - f (a) faktoren (x - a) som er nødvendig for å faktorere. For dette blir det nøye observert hvilke elementer som gjentas i hver faktor av uttrykket.
Selv om Fermat-grensen ikke skiller mellom maksimum og minimum, siden den bare kan identifisere de kritiske punktene i henhold til definisjonen, brukes den ofte til beregning av hetter eller gulv for funksjonene i flyet..
En grunnleggende kunnskap om den grafiske funksjonsteorien i forbindelse med denne teoremet kan være tilstrekkelig til å etablere maksimums- og minimumsverdier mellom funksjonene. Bøyningspunktene kan faktisk defineres ved hjelp av middelverdisetningen i tillegg til Fermats teorem.
Det viktigste paradokset for Fermat kom fra å studere den kubiske parabolen. Fordi hans oppmerksomhet ble rettet mot tangentlinjene til en funksjon for et gitt punkt, løp han inn i problemet med å definere tangentlinjen ved bøyningspunktet i funksjonen.
Det virket umulig å bestemme tangentlinjen til et punkt. Dermed begynner henvendelsen som vil gi opphav til differensialregningen. Definert senere av viktige eksponenter for matematikk.
Studiet av maksimum og minimum for en funksjon var en utfordring for klassisk matematikk, hvor det var nødvendig med en entydig og praktisk metode for å definere disse.
Fermat opprettet en metode basert på driften av små differensialverdier, som etter factoring-prosesser elimineres, og gir vei til den maksimale og minimumsverdien som søkes.
Denne variabelen må evalueres i det opprinnelige uttrykket for å bestemme koordinaten til nevnte punkt, som sammen med analytiske kriterier vil bli definert som maksimum eller minimum for uttrykket.
I sin metode bruker Fermat den bokstavelige symbolikken til Vieta, som besto i den eksklusive bruken av store bokstaver: vokaler, for ukjente og konsonanter for kjente mengder..
Når det gjelder radikale verdier, implementerte Fermat en bestemt prosess, som senere ville bli brukt i faktorisering av grensene for ubestemmelighet uendelig blant uendelig.
Denne prosessen består i å dele hvert uttrykk med verdien av differensialet som brukes. I tilfelle Fermat brukte han bokstaven E, der etter å ha delt med den høyeste kraften i E, ble verdien som ble søkt for det kritiske punktet tydelig..
Fermat-grensen er faktisk et av de minst kjente bidragene i matematikerens lange liste. Studiene hans gikk fra primtallene, for å lage grunnlag for beregningen.
Fermat var i sin tur kjent for sine eksentrisiteter i forhold til hypotesene. Det var vanlig for ham å legge igjen en slags utfordring til de andre matematikerne på den tiden, da han allerede hadde løsningen eller beviset..
Han hadde et stort utvalg av tvister og allianser med forskjellige matematikere på den tiden, som elsket eller hatet å jobbe med ham.
Hans siste setning var hovedansvarlig for verdensberømmelsen, der han uttalte at en generalisering av Pythagoras-teorem for hvilken som helst klasse "n" var det umulig. Han hevdet å ha et gyldig bevis på det, men døde før han offentliggjorde det.
Denne demonstrasjonen måtte vente i omtrent 350 år. I 1995 satte matematikerne Andrew Wiles og Richard Taylor en stopper for angsten Fermat etterlot, og viste at han hadde rett gjennom et gyldig bevis på sin siste setning.
Definer hellingen til tangentlinjen til kurven f (x) = xto på punktet (4, 16)
Å erstatte i uttrykket for Fermat-grensen har vi:
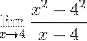
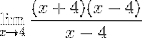
Faktorene (x - 4) er forenklet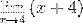
Ved evaluering har du
M = 4 + 4 = 8
Definer det kritiske punktet for uttrykket f (x) = xto + 4 ganger ved bruk av Fermat-grensen
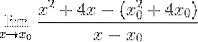
En strategisk gruppering av elementer gjennomføres som søker å gruppere X-X-parene0
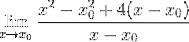
De minste kvadratene er utviklet
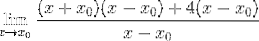
Den vanlige faktoren X-X observeres0 og ekstraheres
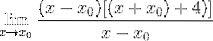
Uttrykket kan nå forenkles og ubestemmelighet brytes
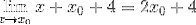
Ved minimumspunktene er det kjent at hellingen til tangentlinjen er lik null. På denne måten kan vi utjevne uttrykket funnet til null og løse verdien X0
2 X0 + 4 = 0
X0 = -4/2 = -2
For å få den manglende koordinaten er det bare nødvendig å evaluere punktet i den opprinnelige funksjonen
F (-2) = (-2)to + 4 (-2) = 4-8 = - 4
Det kritiske punktet er P (-2, -4).
Ingen har kommentert denne artikkelen ennå.