Treghetsformler, ligninger og beregningseksempler

De treghetsmoment av et stivt legeme i forhold til en viss rotasjonsakse, representerer dens motstand mot å endre sin vinkelhastighet rundt aksen. Den er proporsjonal med massen og også til plasseringen av rotasjonsaksen, siden kroppen i henhold til dens geometri kan rotere lettere rundt visse akser enn i andre.

Anta et stort objekt (bestående av mange partikler) som kan rotere rundt en akse. Anta at en styrke virker F, påført tangentielt på masseelementet Δm_Jeg, som produserer et dreiemoment eller moment, gitt av τ_nett = ∑r_Jeg x F_Jeg. Vektoren r_Jeg er posisjonen til Δm_Jeg (se figur 2).

Dette øyeblikket er vinkelrett på rotasjonsplanet (retning +k = kommer ut av papiret). Siden kraften og den radiale posisjonsvektoren alltid er vinkelrett, forblir kryssproduktet:

τ_nett = ∑ F_Jeg r_Jeg k = ∑ (Δm_Jeg til_Jeg) r_Jeg  k = ∑ Δm_Jeg (til_Jeg r_Jeg ) k

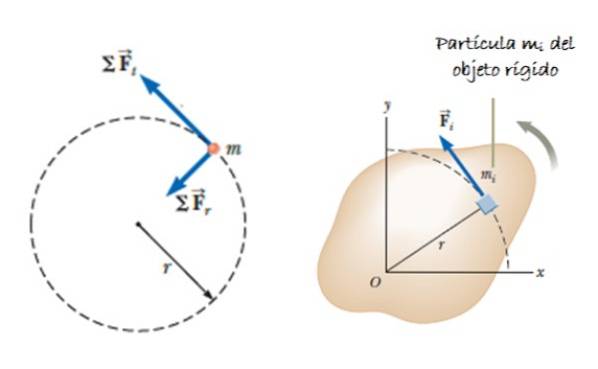
Akselerasjon til_Jeg representerer den tangentielle komponenten av akselerasjon, siden radial akselerasjon ikke bidrar til dreiemoment. Som en funksjon av vinkelakselerasjonen α, kan vi indikere at:

til_Jeg = α r_Jeg

Derfor ser netto dreiemoment slik ut:

τ_nett = ∑ Δm_Jeg (α r_Jeg^to) k = (∑ r_Jeg^to Δm_Jeg) α k

Vinkelakselerasjonen α er den samme for hele objektet, derfor påvirkes den ikke av abonnementet "i" og kan forlate summasjonen, som er nøyaktig treghetsmomentet til objektet symbolisert med bokstaven I:

Jeg = ∑ r_Jeg^to Δm_Jeg

Dette er treghetsmomentet til en diskret massefordeling. Når fordelingen er kontinuerlig, erstattes summeringen med en integral og Δm blir en massedifferensial dm. Integralen utføres over hele objektet:

Jeg = ∫_M(r^to) dm

Enhetene til treghetsmomentet i SI International System er kg x m^to. Det er en skalær og positiv mengde, siden det er produktet av en masse og kvadratet av en avstand.

Artikkelindeks

• 1 Beregningseksempler
  • 1.1 Treghetsmoment for en tynn stang i forhold til en akse som går gjennom sentrum
  • 1.2 Treghetsmoment for en disk i forhold til en akse som går gjennom sentrum
  • 1.3 Treghetsmoment for en solid kule med hensyn til en diameter
  • 1.4 Treghetsmoment for en solid sylinder i forhold til aksialaksen
  • 1.5 Treghetsmoment for et rektangulært ark i forhold til en akse som går gjennom sentrum
  • 1.6 Treghetsmoment for et firkantet ark i forhold til en akse som går gjennom sentrum
• 2 Inerti-teoremer
  • 2.1 Steiners teorem
  • 2.2 Vinkelrett aksesetning
• 3 Øvelsen løst
• 4 Referanser

Beregningseksempler

Et utvidet objekt, for eksempel en stang, disk, kule eller annet, med tetthet ρ er konstant og å vite at tettheten er massevolumforholdet, massedifferansen dm er skrevet som:

ρ = dm / dV → dm = ρdV

Ved å erstatte integralet for treghetsmomentet har vi:

Jeg = ∫r^to ρdV = ρ ∫r^todV

Dette er et generelt uttrykk, gyldig for et tredimensjonalt objekt, hvis volum V og posisjon r er funksjoner til romlige koordinater x, Y Y z. Vær oppmerksom på at tettheten er konstant utenfor integralen.

Tettheten ρ Det er også kjent som volumetrisk tetthet, men hvis objektet er veldig flatt, som et ark eller veldig tynt og smalt som en stang, kan andre former for tetthet brukes, la oss se:

- For et veldig tynt ark er tettheten som skal brukes σ, overflatetettheten (masse per arealeenhet) og gir er arealdifferensial.

- Og hvis det er en tynn stang, der bare lengden er relevant, brukes den lineære massetettheten λ og en lengdeforskjell, i henhold til aksen som brukes som referanse.

I de følgende eksemplene anses alle gjenstander for å være stive (ikke deformerbare) og ha jevn tetthet.

Treghetsmoment for en tynn stang i forhold til en akse som går gjennom sentrum

Her skal vi beregne treghetsmomentet til en tynn, stiv, homogen stang med lengde L og masse M, i forhold til en akse som går gjennom midten.

Først er det nødvendig å etablere et koordinatsystem og bygge en figur med passende geometri, slik:

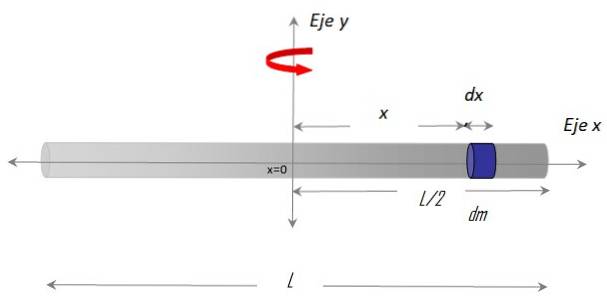
De X-akse langs baren og Akse y som rotasjonsaksen. Fremgangsmåten for å etablere integralen krever også å velge en massedifferensial over stangen, kalt dm, som har en differensiell lengde dx og ligger på posisjonen x vilkårlig, i forhold til sentrum x = 0.

I henhold til definisjonen av lineær massetetthet λ:

λ = M / L

Siden tettheten er jevn, som er gyldig for M og L, er den også gyldig for dm og dx:

λ = dm / dx → dm = λdx.

På den annen side er masseelementet i posisjon x, deretter ved å erstatte denne geometrien i definisjonen, har vi en bestemt integral, hvis grenser er endene på linjen i henhold til koordinatsystemet:

Erstatter den lineære tettheten λ = M / L:

For å finne treghetsmomentet til stangen i forhold til en annen rotasjonsakse, for eksempel en som går gjennom en av ytterpunktene, kan du bruke Steiners teorem (se øvelse løst på slutten) eller utføre en direkte beregning som ligner den vist her, men endrer geometrien på riktig måte.

Treghetsmoment for en disk i forhold til en akse som går gjennom sentrum

En veldig tynn skive med ubetydelig tykkelse er en flat figur. Hvis massen fordeles jevnt over hele overflaten av område A, er massetettheten σ:

σ = M / Y

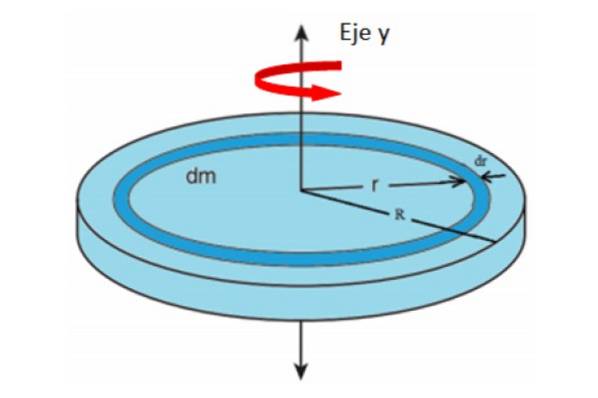
Så mye dm Hva gir tilsvarer massen og arealet til differensialringen vist på figuren. Vi vil anta at hele enheten roterer rundt y-aksen.

Du kan forestille deg at disken er sammensatt av mange konsentriske ringer med radius r, hver med sitt respektive treghetsmoment. Legge til bidragene til alle ringene til de når radiusen R, det totale treghetsmomentet på disken vil være.

σ = dm / dA → dm = σgir

Hvor M representerer hele massen av disken. Området til en disk avhenger av radiusen r som:

A = π.r^to

Avledning med hensyn til r:

dA / dr = 2 = 2π.r → dA = 2π.rdr

Erstatter det ovennevnte i definisjonen av I:

Erstatter σ = M / (π.R^to ) gjenstår:

Treghetsmoment for en solid kule med hensyn til en diameter

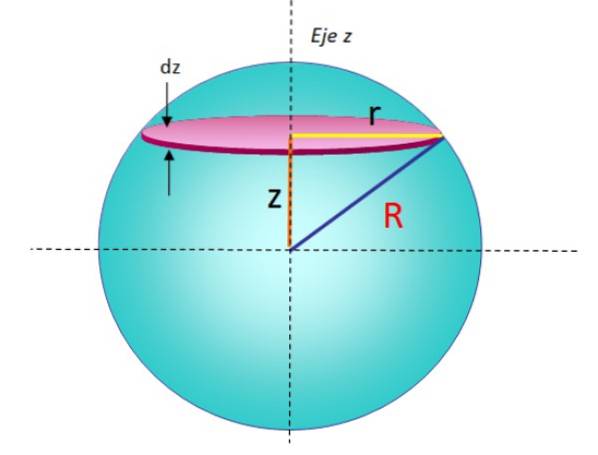
En sfære med radius R kan betraktes som en serie disker stablet oppå hverandre, der hver disk med uendelig liten masse dm, radio r og tykkelse dz, har et treghetsmoment gitt av:

ga_disk = (½) r^todm

For å finne denne differensialen, tok vi ganske enkelt formelen fra forrige avsnitt og erstattet M Y R til dm Y r, henholdsvis. En slik disk kan sees i geometrien i figur 5.

Ved å legge til alle uendelig små treghetsmomenter for stablede skiver oppnås det totale treghetsmomentet til sfæren:

Jeg_sfære = ∫dI_disk

Som tilsvarer:

Jeg = ∫_sfære (½) r^todm

For å løse integralet må du uttrykke dm ordentlig. Som alltid oppnås det fra tettheten:

ρ = M / V = ​​dm / dV → dm = ρ.dV

Volumet til en differensialskive er:

dV = Areal av base x høyde

Skivens høyde er tykkelsen dz, mens området på basen er πr^to, Og dermed:

dV = πr^todz

Og å erstatte den foreslåtte integralen, vil det se slik ut:

Jeg = ∫_sfære(½) r^todm = ∫ (½) r^to(ρπr^todz)

Men før integrering må det observeres at r -radiusen til disken- avhenger av z og R -kulens radius-, som det fremgår av figur 5. Bruk av Pythagoras teorem:

R^to = r^to + z^to → r^to = R^to - z^to

 Som fører oss til:

Jeg = ∫_sfære(½) ρ r^to(πr^todz) = ∫_sfære(½) ρ π r⁴dz= ∫_sfære(½) ρ π (R^to - z^to)^to dz

For å integrere over hele sfæren, bemerker vi at z varierer mellom -R og R, derfor:

Vet det ρ = M / V = ​​M / [(4/3) πR³] endelig er det oppnådd, etter forenkling:

Treghetsmoment for en solid sylinder i forhold til aksialaksen

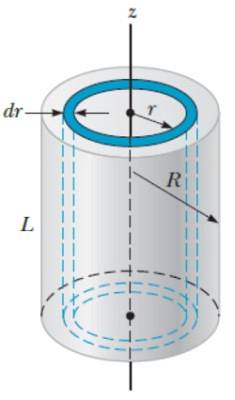
For dette objektet brukes en metode som ligner den som brukes til sfæren, bare denne gangen er det lettere hvis sylinderen er tenkt å være dannet av sylindriske skall med radius r, tykkelse dr og høyde H, som om de var lagene av en løk.

Volumet dV av et sylindrisk lag er:

dV = 2π.rL.dr

Derfor er skallmassen:

dm = ρ.dV = ρ. 2π.r.L.dr

Dette uttrykket er erstattet av definisjonen av treghetsmoment:

Ovennevnte ligning indikerer at sylinderens treghetsmoment ikke avhenger av lengden, men bare av dens masse og radius. Ja L endret, ville treghetsmomentet om den aksiale aksen forbli den samme. Av denne grunn, Jeg av sylinderen sammenfaller med den fra den tidligere beregnede tynne skiven.

Treghetsmoment for et rektangulært ark i forhold til en akse som går gjennom sentrum

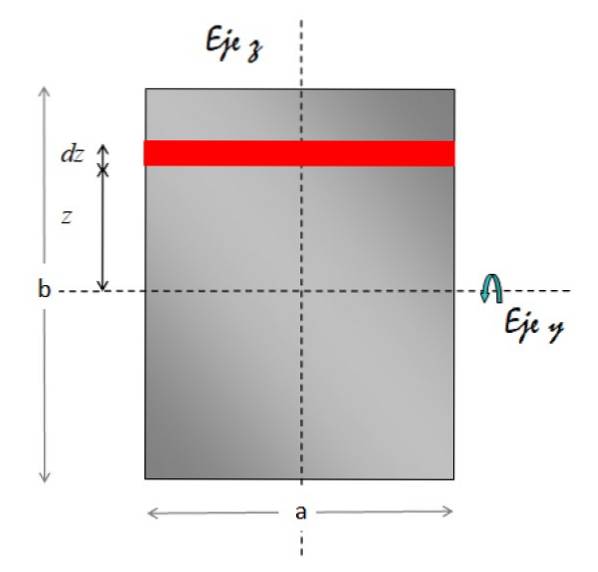
De Akse y horisontal rotasjonsakse. Figuren nedenfor viser geometrien som kreves for å gjennomføre integrasjonen:

Arealelementet merket med rødt er rektangulært. Området er base x høyde, derfor:

dA = a.dz

Derfor er massedifferansen:

dm = σ.dA = σ. (a.dz)

Når det gjelder avstanden fra arealelementet til rotasjonsaksen, er det alltid z. Vi erstatter alt dette integrert av treghetsmomentet:

Nå erstattes overflatemassetettheten σ med:

σ = M / ab

Og det ser definitivt slik ut:

Merk at det er som det med den tynne stangen.

Treghetsmoment for et firkantet ark i forhold til en akse som går gjennom sentrum

For et sidetorg L, i det forrige uttrykket som er gyldig for et rektangel, er det bare å erstatte verdien av b for den av L:

Moment of Inertia Theorems

Det er to teoremer som er spesielt nyttige for å forenkle beregningen av treghetsmomenter om andre akser, som ellers kan være vanskelig å finne på grunn av manglende symmetri. Disse setningene er:

Steiners teorem

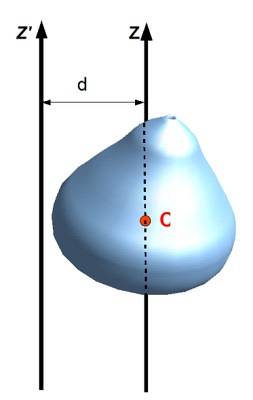
Også kalt teori for parallelle akser, relaterer treghetsmomentet i forhold til en akse med en annen som passerer gjennom massesenteret til objektet, så lenge aksene er parallelle. For å bruke den er det nødvendig å kjenne avstanden D mellom begge akser og selvfølgelig massen M til objektet.

Være Jeg_z treghetsmomentet til et utvidet objekt med hensyn til z-aksen, jeg_CM treghetsmomentet med hensyn til en akse som passerer gjennom massesenteret (CM) til nevnte objekt, så er det sant at:

Jeg_z = Jeg_CM + MD^to

Eller i notasjonen av følgende figur: Jeg_{z '} = Jeg_z + Md^to

Vinkelrett aksesetning

Denne setningen blir brukt på plane overflater og går slik: treghetsmomentet til et plan objekt rundt en akse vinkelrett på den er summen av treghetsmomentene rundt to akser vinkelrett på den første aksen:

Jeg_z = Jeg_x + Jeg_Y

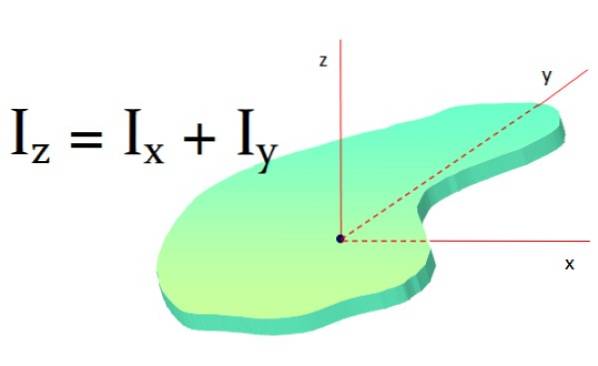
Hvis objektet har en slik symmetri Jeg_x og Jeg_Y er like, så er det sant at:

Jeg_z = 2I_x

Treningen løst

Finn treghetsmomentet til stangen i forhold til en akse som går gjennom en av endene, som vist i figur 1 (under og til høyre) og figur 10.

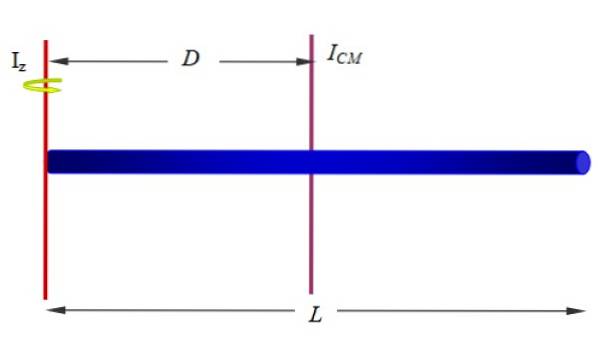
Løsning:

Vi har allerede treghetsmomentet til stangen rundt en akse som går gjennom dens geometriske sentrum. Siden stangen er homogen, er dens massesenter på det tidspunktet, så dette vil være vårt Jeg_CM å anvende Steiners teorem.

Hvis lengden på stangen er L, z-aksen er på en avstand D = L / 2, derfor:

Jeg_z = Jeg_CM + MD^to= (1/12) ML^to+M (L / 2)^to= (1/3) ML^to

Referanser

1. Bauer, W. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill. 313-340
2. Rex, A. 2011. Fundamentals of Physics. Pearson. 190-200.
3. Parallell aksesetning. Gjenopprettet fra: hyperphysics.phy-astr.gsu.edu.
4. Serway, R. 2018. Physics for Science and Engineering. Volum 1. Cengage.
5. Sevilla universitet. Treghetsmoment av sfæriske faste stoffer. Gjenopprettet fra: laplace.us.es.
6. Sevilla universitet. Treghetsmoment for et partikelsystem. Gjenopprettet fra: laplace.us.es.
7. Wikipedia. Parallellakssetning. Gjenopprettet fra: en.wikipedia.org