
Uniform sirkulær bevegelse (M.C.U.) formler, egenskaper

En partikkel har sirkulær bevegelse uniform (M.C.U.) når banen er en omkrets og den også kjører den med konstant hastighet. Mange gjenstander som deler av maskiner og motorer, for eksempel, har denne typen bevegelse, blant annet datamaskinharddisker, vifteblad, sjakter og mange andre ting skiller seg ut..
Ensartet sirkelbevegelse er også en god tilnærming for bevegelsen til noen himmellegemer som jorden. Egentlig er jordens bane elliptisk, som indikert av Keplers lover. Banens eksentrisitet er imidlertid liten, og som en første tilnærming kan den betraktes som sirkulær, noe som forenkler noen beregninger, for eksempel å finne jordens hastighet når den beveger seg rundt solen..
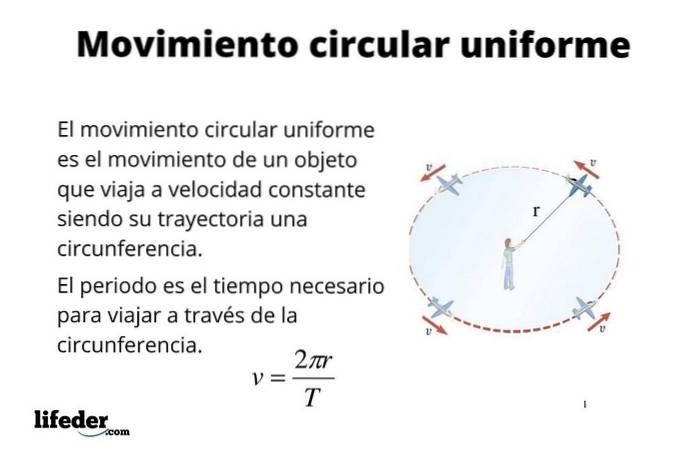
I beskrivelsen av ensartet sirkelbevegelse brukes de samme parametrene som i rettlinjet bevegelse, nemlig: posisjon, forskyvning, tid, hastighet og akselerasjon..
Akselerasjon? Ja, ja, jevn sirkulær bevegelse akselereres, selv om hastigheten er v være konstant. Dette er fordi hastigheten v, som er en vektor, og det er derfor den er fet, og endrer kontinuerlig retning når objektet eller partikkelen roterer. Enhver endring i v produseres av en akselerasjon, som, som det vil sees, er rettet mot sentrum av sirkelbanen.
Ensartet sirkelbevegelse er bevegelse i planet xy, derfor er det en bevegelse i to dimensjoner. Det er imidlertid mulig å uttrykke det mer komfortabelt ved hjelp av vinkelen θ som partikkelen feier, målt i forhold til den horisontale aksen eller en annen passende referanseakse..
Selv om det er et utvidet objekt, sveiper partiklene alltid i samme vinkel, selv om de har forskjellige koordinater. (x, y).
Artikkelindeks
- 1 Egenskaper for ensartet sirkulær bevegelse
- 2 Formler for jevn sirkulær bevegelse
- 2.1 Posisjonsvektor
- 2.2 Vinkelhastighet og lineær hastighet
- 2.3 Sentripetal akselerasjon
- 2.4 Periode og frekvens
- 3 Eksempler på ensartet sirkulær bevegelse
- 3.1 Jordens bevegelse
- 3.2 Partikler på kanten av en disk
- 3.3 Hubble-romteleskop
- 3.4 Sentrifuger
- 3.5 Hagesprinkler
- 3.6 Sport
- 4 Øvelse løst
- 5 Referanser
Kjennetegn ved ensartet sirkulær bevegelse
Egenskapene til ensartet sirkulær bevegelse kan oppsummeres som følger:
-Banen er en omkrets, derfor er den en bevegelse i planet.
-Farten v er konstant, men hastigheten v nei, fordi det kontinuerlig endrer retning og retning for å imøtekomme mobilens sving.
-Hastighetsvektoren v er alltid tangensiell for omkretsen og vinkelrett på radiell retning.
-Vinkelhastigheten ω er konstant.
-Til tross for å være ensartet, er det en akselerasjon for å forklare disse endringene i hastighetsretningen. Denne akselerasjonen er sentripetal akselerasjon.
-Sentripetal akselerasjon og hastighet er vinkelrett på hverandre.
-Det er en periodisk eller repeterende bevegelse, derfor er periode- og frekvensstørrelser definert for den.
Ensartede sirkulære bevegelsesformler
I dette skjemaet er det en partikkel P som spinner mot klokken med MCU, i henhold til retning og følelse av hastighetsvektoren v tegnet.
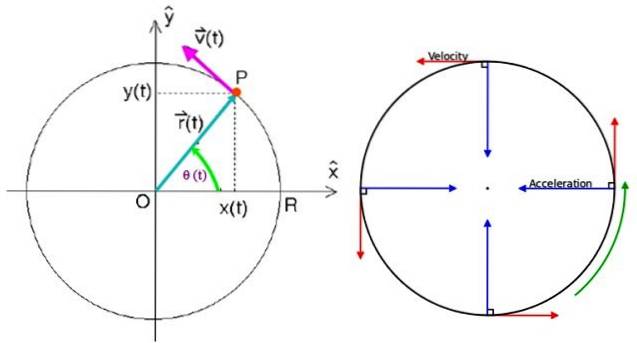
For å spesifisere posisjonsvektoren er det nødvendig å ha et referansepunkt, og det ideelle punktet er sentrum av omkretsen O som sammenfaller med sentrum av det kartesiske koordinatsystemet i xy-planet.
Posisjonsvektor
Det er betegnet som r (t) og er rettet fra opprinnelsen til punktet P hvor partikkelen er lokalisert. På et gitt øyeblikk, i kartesiske koordinater, er det skrevet som:
r (t) = x (t) Jeg + og T) j
Hvor Jeg Y j er enhetsvektorene vinkelrett i retningene x og Y henholdsvis. Fra grafen kan det sees at vektormodulen r (t) alltid verdt R, omkretsens radius. Hvis θ er dannet vinkelen r med den horisontale aksen er posisjonen lik:
r (t) = [Rcos θ(t)] Jeg +[Rsen θ(t)] j
Vinkelen den danner r (t) med den horisontale aksen er en sentral vinkel og verdien er:
θ = s / R
Hvor s er omkretsbuen reist og R radius. Sa vinkelen θ er en funksjon av tid, så den kan skrives θ = θ (t), anrop vinkelposisjon.
Siden hastigheten er konstant, beskriver partikkelen like vinkler i like tider og i analogi med den ensartede rettlinjede bevegelsen, skrives det:
θ = θ (t) = θeller + .t
Her θeller er den opprinnelige vinkelen målt i radianer i forhold til referanseaksen, den kan være 0 eller en hvilken som helst verdi og ω er vinkelhastigheten.
Vinkelhastighet og lineær hastighet
Vinkelhastighet er det første derivatet av vinkelposisjon og betegnes som ω. Verdien er konstant for jevn sirkelbevegelse, siden like vinkler feies på like tid. Med andre ord:

Enhetene med lineær hastighet i jevn sirkelbevegelse er de samme som for lineær bevegelse: m / s (i SI International System), km / t, cm / s og andre..
Sentripetal akselerasjon
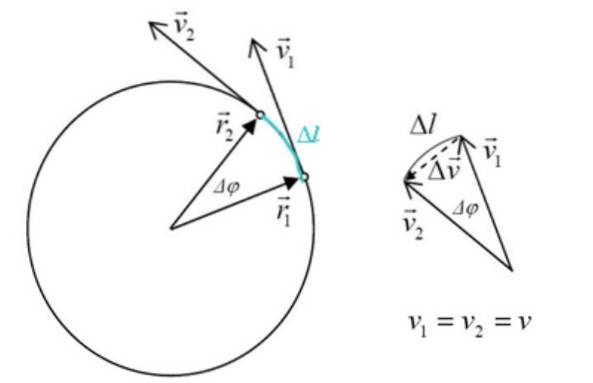
I figuren nedenfor er det en partikkel som beveger seg med klokken rundt omkretsen med konstant hastighet. Dette betyr at hastighetsvektoren alltid har samme modul, men den endrer retning for å imøtekomme omkretsen.

Enhver endring i hastighet resulterer i akselerasjon, som per definisjon er:

Trekanten dannet av vto, v1 og Δv ligner sidetrekanten rto, r1 og Δl, hvor Δφ er den sentrale vinkelen. Størrelsen på rto Y r1 de er de samme, så:
rto = r1 = r
Så, av begge trekanter, har vi disse forholdene for vinkelen:
Δφ = Δr / r; Δφ = Δv / v
Den fete typen er ikke nødvendig, siden målingen på vinkelen avhenger av størrelsen på disse vektorene. Som samsvarer med de foregående uttrykkene, følger det at:





Periode og frekvens
Siden sirkelbevegelsen er repeterende, er perioden definert T det samme som tiden det tar for mobilen å gjøre en hel sving. Siden lengden på omkretsen av radius R er 2πR, er vinkelen feid i radianer på full sving 2π radianer, og det tar tid T, er vinkelhastigheten:
ω = 2π / T
T = 2π / ω
Perioden med ensartet sirkulær bevegelse måles i sekunder i det internasjonale systemet.
For sin del frekvensen F er antall svinger per tidsenhet og er den gjensidige eller omvendte av perioden:
f = n / t = 1 / T
Frekvensenheten i det internasjonale systemet er s-1.
Eksempler på ensartet sirkelbevegelse
Mange gjenstander roterer for å gi forskjellige effekter: hjul, skiver og turbiner. Når driftshastigheten er nådd, utføres rotasjonen vanligvis med konstant hastighet. Sirkulær bevegelse er så vanlig i hverdagen at du nesten aldri tenker på det, så her er noen nære eksempler som illustrerer det veldig bra:
Jordens bevegelse

Jorden og de andre planetene i solsystemet beveger seg i elliptiske baner med liten eksentrisitet, bortsett fra kvikksølv, noe som betyr at det i første tilnærming kan antas at deres bevegelse er ensartet sirkulær.
Med dette har du en god ide om oversettelseshastigheten rundt solen, siden bevegelsesperioden i Jorden er kjent: ett år eller 365 dager..
Partikler på kanten av en disk

Partiklene som roterer på kanten av en gammel platespiller eller bladet til en vifte, følger en jevn sirkelbevegelse når enheten når avspillingshastigheten..
Hubble romteleskop

Hubble-romteleskopet sirkler jorden rundt 7550 m / s.
Sentrifuger
Vaskemaskinene utfører en spinningsprosess for å klemme på klærne, som består av å rotere beholdertrommelen i høy hastighet. Tørketrommelene roterer også i en jevn sirkelbevegelse..
Sentrifugering brukes også i laboratorier for å skille forbindelser, for eksempel, og dermed skille bestanddelene av dem ved forskjell i tetthet. Hver gang vi snakker om sentrifugering, er det en sirkelbevegelse som er jevn, i det minste en stund.
Hagevannbokser
Mange hagespredere roterer med konstant hastighet slik at bakken blir vannet jevnt..
sport

I for eksempel hammerkastet, som er en olympisk disiplin, snurrer utøveren en metallkule med kraft ved hjelp av en stålkabel festet til grepet. Målet er å sende ballen så langt som mulig, men uten å forlate et bestemt område.
Treningen løst
En partikkel beveger seg i en omkrets på radius 2m med konstant hastighet v = 8 m / s, mot urviseren. Opprinnelig var partikkelen i r = +2 j m. Regne ut:
a) Vinkelhastigheten ω
b) Dens vinkelposisjon θ (t)
c) Bevegelsesperioden
d) Sentripetal akselerasjon.
e) Partikkelens posisjon etter å ha passert t = π / 4 s
Løsning til
Fra formelen v = Rω følger det at:
ω = v / R = (8 m / s) / 2m = 4rad ∙ s-1
Løsning b
Tar den positive x-aksen som referanseakse, er partikkelen i utgangspunktet 90 ° = π / 2 radianer i forhold til aksen, siden uttalelsen sier at utgangsposisjonen er +2 j m, det vil si at partikkelen er på y = 2m når bevegelsen begynner å følge.
θ = θ (t) = θeller + ωt = π / 2 + 4t
Løsning c
T = 2π / ω = 2π / 4 s = 0,5 π s
Løsning d
a = vto / R = (8 m / s)to / 2 m = 32 m / sto
Løsning e
θ (t) = π / 2 + 4t → θ (π / 4) = π / 2 + 4 ∙ (π / 4) = 3π / 2 radianer
Dette betyr at partikkelen etter den tiden er i posisjonen y = -2m j. Det er fornuftig fordi t = π / 4 s er halve perioden, derfor beveget partikkelen en 180 ° vinkel mot urviseren fra utgangsposisjonen, og den må være i motsatt posisjon.
Referanser
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysikk. 2. plass. Ed. McGraw Hill.
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 1. Pearson.
- Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.
- Zapata, F. Sirkulær bevegelse. Gjenopprettet fra: francesphysics.blogspot.com.



Ingen har kommentert denne artikkelen ennå.