Archimedes of Syracuse (287 f.Kr. - 212 f.Kr.) var en gresk matematiker, fysiker, oppfinner, ingeniør og astronom fra den antikke byen Syracuse, på øya Sicilia. Hans mest fremragende bidrag er Archimedean-prinsippet, utviklingen av utmattelsesmetoden, den mekaniske metoden eller etableringen av det første planetariet..
Han regnes for tiden som en av de tre viktigste figurene i gammel matematikk sammen med Euklid og Apollonius, siden deres bidrag betydde viktige vitenskapelige fremskritt for tiden innen områdene kalkulator, fysikk, geometri og astronomi. Dette gjør ham igjen til en av de mest fremtredende forskerne i menneskets historie..
Til tross for at få detaljer om hans personlige liv er kjent - og de som er kjent er av tvilsom pålitelighet -, er hans bidrag kjent takket være en serie brev skrevet om hans arbeid og prestasjoner som har blitt bevart til i dag, som tilhører korrespondansen han holdt i mange år med venner og andre matematikere fra den tiden.
Archimedes var kjent i sin tid for sine oppfinnelser, som vakte stor oppmerksomhet fra hans samtid, delvis fordi de ble brukt som krigsutstyr for å forhindre mange romerske invasjoner..
Imidlertid skal han ha hevdet at det eneste som var veldig viktig var matematikk, og at hans oppfinnelser bare var et produkt av hobbyen med anvendt geometri. Ettertiden har hans arbeider innen ren matematikk vært mye mer verdsatt enn hans oppfinnelser..
Artikkelindeks
Archimedes av Syracuse ble født i ca 287 f.Kr. Det er ikke kjent mye informasjon om hans tidlige år, selv om det kan sies at han ble født i Syracuse, en by som regnes som den viktigste havnen på øya Sicilia, i dag i Italia..
På den tiden var Syracuse en av byene som utgjorde den såkalte Magna Grecia, som var plassen bebodd av nybyggere av gresk opprinnelse mot det sørlige området av den italienske halvøya og på Sicilia..
Ingen spesifikk informasjon er kjent om Archimedes 'mor. I forhold til faren er det kjent at dette ble kalt Phidias og at han var viet astronomi. Denne informasjonen om faren er kjent takket være et fragment av boka Sanddisken, skrevet av Archimedes, der han nevner farens navn.
Heraclides, som var en gresk filosof og astronom, var nære venner med Archimedes og skrev til og med en biografi om ham. Dokumentet er imidlertid ikke bevart, så all informasjonen deri er ukjent..
På den annen side indikerte historikeren, filosofen og biografen Plutarch i sin bok med tittelen Parallel Lives at Archimedes hadde et blodforhold med Hiero II, en tyrann som hadde kommandoen i Syracuse siden 265 f.Kr..
Som et resultat av den lille informasjonen vi har om Archimedes, er det ikke kjent med sikkerhet hvor han fikk sin første trening..
Ulike historiografer har imidlertid bestemt at det er stor mulighet for at Archimedes studerte i Alexandria, som var det viktigste greske kultur- og undervisningssenteret i regionen..
Denne antagelsen støttes av informasjon gitt av den greske historikeren Diodorus Siculus, som antydet at Archimedes sannsynligvis studerte i Alexandria.
I tillegg nevner Archimedes selv mange forskere fra den tiden hvis arbeid var konsentrert i Alexandria, i mange av hans verk, så det kan antas at han faktisk utviklet seg i den byen..
Noen av personlighetene som Archimedes antas å ha samhandlet med i Alexandria, er geografen, matematikeren og astronomen Eratosthenes fra Cyrene, og matematikeren og astronomen Conon de Sanos..
På den annen side kan det faktum at faren til Archimedes var astronom, ha hatt en betydelig innflytelse på tilbøyeligheter som han senere demonstrerte, fordi senere og fra en ung alder, en spesiell tiltrekning mot fagområdet.
Etter tiden i Alexandria anslås det at Archimedes vendte tilbake til Syracuse.
Etter at han kom tilbake til Syracuse, begynte Archimedes å utvikle forskjellige gjenstander som veldig snart fikk ham til å oppnå popularitet blant innbyggerne i denne byen. I denne perioden ga han seg helt til vitenskapelig arbeid, produserte forskjellige oppfinnelser og utledet ulike matematiske forestillinger i god tid før sin tid..
For eksempel, ved å studere egenskapene til solide buede og plane figurer, kom han til å heve konsepter relatert til integral- og differensialregning, som ble utviklet senere.
På samme måte var Archimedes den som definerte at volumet assosiert med en kule tilsvarer det dobbelte av størrelsen på sylinderen som inneholder den, og han var den som oppfant den sammensatte remskiven, basert på hans oppdagelser om loven om spaken..
I løpet av året 213 f.Kr. kom romerske soldater inn i byen Syracuse og omringet bosetterne for å få dem til å overgi seg..
Denne handlingen ble ledet av det greske militæret og politikeren Marco Claudio Marcelo innenfor rammen av den andre puniske krigen. Senere ble det kjent som Roma-sverdet, siden det endte med å erobre Syracuse.
Midt i konflikten, som varte i to år, kjempet innbyggerne i Syracuse mot romerne med mot og voldsomhet, og Archimedes spilte en veldig viktig rolle, siden han viet seg til å lage verktøy og instrumenter som ville bidra til å beseire romerne..
Til slutt tok Marco Claudio Marcelo byen Syracuse. Før den store intelligensen til Archimedes beordret Marcelo strengt at de ikke skulle såre eller drepe ham. Imidlertid ble Archimedes drept av en romersk soldat.
Archimedes døde i 212 f.Kr. Mer enn 130 år etter hans død, i 137 f.Kr., okkuperte forfatteren, politikeren og filosofen Marco Tulio Cicero en stilling i Roma-administrasjonen og ønsket å finne graven til Archimedes..
Denne oppgaven var ikke lett, fordi Cicero ikke kunne finne noen som angav den nøyaktige plasseringen. Imidlertid fikk han det til slutt, veldig nær Agrigento-porten og i beklagelig tilstand.
Cicero ryddet graven og oppdaget at en kule var innskrevet i en sylinder, som en referanse til oppdagelsen om volumet som Archimedes gjorde for en tid tilbake..
En av versjonene sier at Archimedes var midt i å løse et matematisk problem da han ble kontaktet av en romersk soldat. Det sies at Archimedes kan ha bedt ham litt tid på å løse problemet, så soldaten ville ha drept ham.
Den andre versjonen ligner den første. Det forteller at Archimedes løste et matteproblem da byen ble tatt.
En romersk soldat kom inn i forbindelsen hans og beordret ham til å møte Marcelo, som Archimedes svarte og sa at han først måtte løse problemet han jobbet med. Soldaten ble opprørt som et resultat av dette svaret og drepte ham.
Denne hypotesen indikerer at Archimedes hadde i sine hender et stort mangfold av matematiske instrumenter. Så så en soldat ham og tenkte at han kunne ha med seg verdifulle gjenstander, så han drepte ham.
Denne versjonen illustrerer at Archimedes ble krøpet nær bakken og tenkte på noen planer han studerte. Tilsynelatende kom en romersk soldat bakfra, og uvitende om at det var Archimedes, skjøt ham.
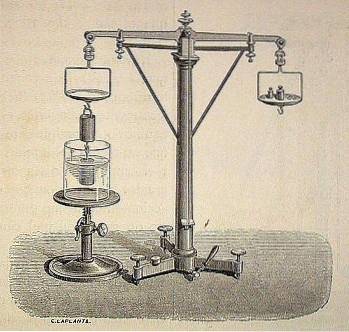
Archimedean-prinsippet betraktes av moderne vitenskap som en av de viktigste arvene fra den gamle tiden.
Gjennom historien og muntlig har det blitt overført at Archimedes kom til sin oppdagelse ved et uhell takket være at kong Hieron ga ham i oppdrag å sjekke om en gullkrone, bestilt til å bli produsert av ham, bare var laget av gullreng og ikke inneholdt noe annet metall . Jeg måtte gjøre dette uten å ødelegge kronen.
Det sies at mens Archimedes mediterte over hvordan han skulle løse dette problemet, bestemte han seg for å ta et bad, og da han kom inn i badekaret, skjønte han at vannstanden økte da han senket seg i det..
På denne måten ville han komme til å oppdage det vitenskapelige prinsippet som sier at "hver kropp helt eller delvis nedsenket i en væske (væske eller gass) mottar et trykk oppover, lik vekten av væsken som løsnes av objektet".
Dette prinsippet betyr at væsker utøver en oppadgående kraft - skyver oppover - på en hvilken som helst gjenstand nedsenket i dem, og at mengden av denne skyvekraften er lik vekten av væsken forskjøvet av det nedsenket legemet, uavhengig av vekten..
Forklaringen på dette prinsippet beskriver fenomenet flotasjon, og finnes i dets Avhandling om flytende kropper.
Archimedes 'prinsipp har blitt brukt enormt i ettertiden for flotering av gjenstander til massebruk, som ubåter, skip, livreddere og luftballonger..
En annen av Archimedes viktigste bidrag til vitenskapen var inkluderingen av en rent mekanisk - det vil si teknisk metode i resonnementet og argumentasjonen av geometriske problemer, som betydde en enestående måte å løse denne typen problemer for tiden..
I sammenheng med Archimedes ble geometri ansett som en utelukkende teoretisk vitenskap, og det vanlige var at ren matematikk kom ned mot andre praktiske vitenskap der dens prinsipper kunne brukes..
Av denne grunn blir det i dag ansett som forløperen til mekanikk som en vitenskapelig disiplin..
I skrivingen der matematikeren eksponerer den nye metoden for sin venn Eratosthenes, indikerer han at den tillater oss å ta opp spørsmål om matematikk gjennom mekanikk, og at det på en bestemt måte er lettere å konstruere beviset på et geometrisk teorem hvis det er har allerede noen tidligere praktiske kunnskaper, at hvis du ikke aner om det.
Denne nye forskningsmetoden utført av Archimedes ville bli en forløper for det uformelle stadiet for oppdagelse og hypoteseformulering av den moderne vitenskapelige metoden..
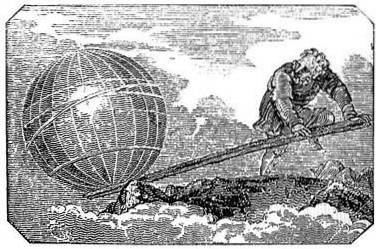
Selv om spaken er en enkel maskin som ble brukt lenge før Archimedes, var det han som formulerte prinsippet som forklarer driften i hans avhandling om balansen mellom fly.
Ved formuleringen av denne loven etablerer Archimedes prinsipper som beskriver en spaks forskjellige oppførsel når han plasserer to kropper på den, avhengig av deres vekt og avstand fra støttepunktet..
På denne måten påpeker han at to kropper som kan måles (forholdsvis), plassert på en spak, balanserer når de er i avstander omvendt proporsjonal med vekten..
På samme måte gjør umålelige legemer det (som ikke kan måles), men denne loven ble påvist av Archimedes bare med kropper av den første typen.
Hans formulering av prinsippet om spaken er et godt eksempel på anvendelsen av den mekaniske metoden, ettersom han forklarte i et brev adressert til Dositeo, ble det først oppdaget gjennom mekaniske metoder som han praktiserte.
Senere formulerte han dem ved hjelp av geometriske metoder (teoretisk). Denne eksperimenteringen på legemer ga også oppfatningen om tyngdepunktet..
Utmattelsen er en metode som brukes i geometri som består av tilnærming av geometriske figurer hvis område er kjent, ved hjelp av inskripsjonen og omskrivningen, over noen andre hvis område det er ment å vite.
Selv om Archimedes ikke var skaperen av denne metoden, utviklet han den mesterlig og klarte å beregne en nøyaktig verdi av Pi ved hjelp av den.
Archimedes, ved bruk av utmattelsesmetoden, innskrevet og omskrevne sekskanter til en omkrets med diameter 1, og reduserte til absurditet forskjellen mellom sekskantområdet og omkretsen..
For å gjøre dette, halverte han sekskantene som skapte polygoner med opptil 16 sider, som vist i forrige figur..
På denne måten kom han til å spesifisere at verdien til pi (av forholdet mellom lengden på en omkrets og dens diameter) er mellom verdiene 3.14084507… og 3.14285714… .
Archimedes brukte mesterlig metoden for utmattelse fordi han ikke bare klarte å nærme seg beregningen av Pi-verdien med en ganske lav feilmargin, og derfor ønsket, men også fordi Pi er et irrasjonelt tall gjennom denne metoden og de oppnådde resultatene la grunnlaget som ville spire i det uendelige kalkulatorsystemet, og senere, i den moderne integrerte kalkulus.
For å bestemme arealet til en sirkel, brukte Archimedes en metode som besto av å tegne en firkant som passet nøyaktig inne i en sirkel.
Da han visste at området på torget var summen av sidene, og at sirkelområdet var større, begynte han å arbeide for å oppnå tilnærminger. Han gjorde dette ved å erstatte firkantet en 6-sidig polygon og deretter jobbe med mer komplekse polygoner.
Archimedes var den første matematikeren i historien som kom nærme å gjøre en seriøs beregning av tallet Pi.
Blant de ni avhandlingene som kompilerer arkimedes arbeid i matematikk og fysikk, er det to bind på geometrien til kuler og sylindere.
Dette arbeidet handler om bestemmelsen om at overflaten til enhver radiuskule er fire ganger den største sirkelen, og at volumet til en kule er to tredjedeler av sylinderen der den er innskrevet..
Også kjent som kilometer-telleren, var det en oppfinnelse av denne berømte mannen.
Denne enheten ble bygget basert på prinsippet om et hjul som aktiverer tannhjul som gjør at den tilbakelagte avstanden kan beregnes når den roterer.
I følge dette samme prinsippet designet Archimedes forskjellige typer kilometerteller for militære og sivile formål..
Basert på vitnesbyrdet fra mange klassiske forfattere som Cicero, Ovidius, Claudian, Marciano Capela, Cassiodorus, Sextus Empiricus og Lactantius, tilskriver mange forskere i dag etableringen av det første rudimentære planetariet til Archimedes..
Det er en mekanisme som består av en serie "kuler" som klarte å etterligne planetenes bevegelse. Så langt er detaljene i denne mekanismen ukjent.
I følge Cicero var planetariumene bygget av Archimedes to. I en av dem var jorden og de forskjellige konstellasjonene i nærheten representert.
I den andre, med en enkelt rotasjon, utførte solen, månen og planetene sine egne og uavhengige bevegelser i forhold til faste stjerner på samme måte som de gjorde på en ekte dag. I sistnevnte kunne man i tillegg observere suksessive faser og formørkelser.
Archimedean-skruen er en enhet som brukes til å føre vann fra bunnen opp gjennom en skråning, ved hjelp av et rør eller en sylinder.
I følge den greske historikeren Diodorus ble takket være denne oppfinnelsen vanning av fruktbare landområder langs Nilen i det gamle Egypt gjort lettere, siden tradisjonelle verktøy krevde en enorm fysisk innsats som utmattet arbeiderne.
Sylinderen som brukes har innsiden av en skrue med samme lengde, som opprettholder sammenkoblet et system av propeller eller finner som utfører en roterende bevegelse som drives manuelt av en roterende spak.
På denne måten klarer propellene å skyve ethvert stoff fra bunnen og danne en slags uendelig krets.
Archimedes 'klo, eller jernhånden som den også er kjent, var et av de mest fryktinngytende krigsvåpenene som ble opprettet av denne matematikeren, og ble den viktigste for forsvaret av Sicilia fra romerske invasjoner..
Ifølge forskning fra professorene ved Drexel University Chris Rorres (Institutt for matematikk) og Harry Harris (Institutt for anleggsteknikk og arkitektur) var det en stor spak som hadde en gripekrok festet til spaken. Ved hjelp av en kjede som hang fra den.
Gjennom spaken ble kroken manipulert slik at den falt på fiendens skip, og målet var å hekte den og heve den til et slikt punkt at den når den slippes ville være i stand til å velte den, eller få den til å krasje mot steiner i fjæra..
Rorres og Harris presenterte på symposiet "Extraordinary Machines and Structures of Antiquity" (2001), en miniatyrrepresentasjon av denne gjenstanden med tittelen "A formidable war machine: Construction and operation of Archimedes 'iron hand"
For å utføre dette arbeidet stolte de på argumentene fra de gamle historikerne Polybius, Plutarch og Tito Livio..
Ingen har kommentert denne artikkelen ennå.