De rectilineal bevegelse er den der mobilen beveger seg langs en rett linje og derfor kjører i en dimensjon, derfor kalles den også endimensjonal bevegelse. Denne rette linjen er bane eller sti fulgt av objektet i bevegelse. Biler som beveger seg langs alléen i figur 1 følger denne typen bevegelse.
Det er den enkleste bevegelsesmodellen du kan forestille deg. De daglige bevegelsene til mennesker, dyr og ting kombinerer vanligvis bevegelser i en rett linje med bevegelser langs kurver, men noen som utelukkende er rettlinjede blir ofte observert.
Her er noen gode eksempler:
- Når du løper langs et 200 meter rett spor.
- Å kjøre bil på rett vei.
- Å slippe et objekt fritt fra en viss høyde.
- Når en ball kastes loddrett oppover.
Nå oppnås målet med å beskrive en bevegelse ved å spesifisere egenskaper som:
- Posisjon
- Forskyvning
- Hastighet
- Akselerasjon
- Vær.
For at en observatør skal oppdage bevegelsen til et objekt, må de ha et referansepunkt (opprinnelsen O) og ha etablert en bestemt retning å bevege seg i, som kan være aksen x, aksen Y eller andre.
Når det gjelder objektet som beveger seg, kan det ha et uendelig antall former. Det er ingen begrensninger i denne forbindelse, men i alt som følger vil det antas at mobilen er en partikkel; et objekt så lite at dimensjonene ikke er relevante.
Dette er kjent for ikke å være tilfelle for makroskopiske objekter; det er imidlertid en modell med gode resultater for å beskrive den globale bevegelsen til et objekt. På denne måten kan en partikkel være en bil, en planet, en person eller andre gjenstander som beveger seg.
Vi vil begynne studien vår av rettlinjet kinematikk med en generell tilnærming til bevegelse, og spesielle tilfeller som de som allerede er nevnt vil bli studert..
Artikkelindeks
Følgende beskrivelse er generell og gjelder for alle typer endimensjonale bevegelser. Det første er å velge et referansesystem. Linjen langs hvilken bevegelsen foregår vil være aksen x. Bevegelsesparametere:
Det er vektoren som går fra opprinnelsen til det punktet hvor objektet er på et gitt øyeblikk. I figur 2, vektoren x1 indikerer posisjonen til mobilen når den er i koordinaten P1 og han i tide t1. Enhetene til posisjonsvektoren i det internasjonale systemet er meter.
Forskyvningen er vektoren som indikerer endring i posisjon. I figur 3 har bilen flyttet seg fra stilling P1 å posisjonere Pto, derfor er forskyvningen Δx = xto - x1. Forskyvningen er subtraksjonen av to vektorer, den er symbolisert med den greske bokstaven Δ (“delta”) og den er i sin tur en vektor. Enhetene i det internasjonale systemet er meter.
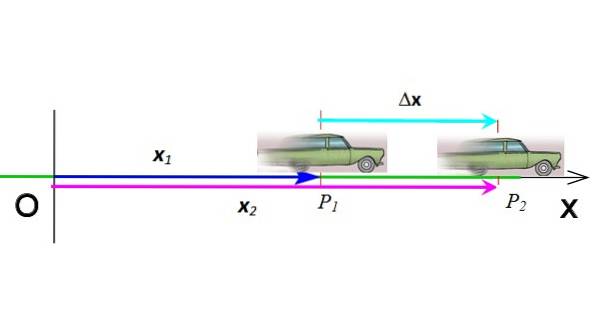
Vektorer er angitt med fet skrift i trykt tekst. Men å være på samme dimensjon, hvis du vil, kan du gjøre uten vektornotasjonen.
Avstand d reist av det bevegelige objektet er den absolutte verdien av forskyvningsvektoren:
d = ΙΔxΙ = Δx
Å være en absolutt verdi, er den tilbakelagte avstanden alltid større enn eller lik 0, og enhetene er de samme som for posisjon og forskyvning. Absolutt verdinotering kan gjøres med modulostenger eller ganske enkelt ved å fjerne fet skrift i trykt tekst.
Hvor raskt endrer stillingen seg? Det er langsomme og raske mobiler. Nøkkelen har alltid vært fart. For å analysere denne faktoren blir posisjonen analysert x tidens funksjon t.
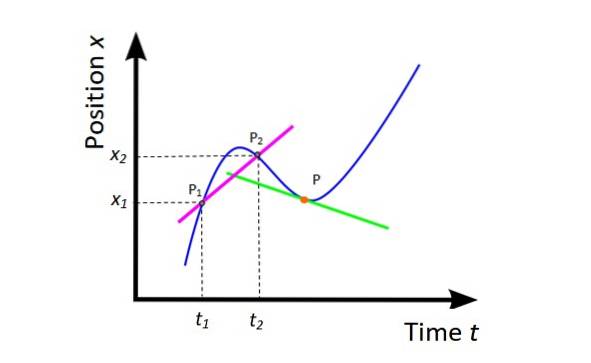
Gjennomsnittshastighet vm (se figur 4) er skråningen til secantlinjen (fuchsia) til kurven x vs. t og gir global informasjon om bevegelsen til mobilen i det vurderte tidsintervallet.
vm = (xto - x1) / (tto -t1) = Δx / Δt
Gjennomsnittlig hastighet er en vektor hvis enheter i det internasjonale systemet er meter / sekund (m / s).
Gjennomsnittlig hastighet beregnes ved å ta et målbart tidsintervall, men rapporterer ikke hva som skjer innenfor det intervallet. For å vite hastigheten når som helst, må du gjøre tidsintervallet veldig lite, matematisk tilsvarer det å gjøre:
Δt → 0
Ligningen ovenfor er gitt for gjennomsnittshastigheten. På denne måten oppnås øyeblikkelig hastighet eller bare hastighet:
Geometrisk er den avledede av posisjonen med hensyn til tid skråningen av linjen som tangerer kurven x vs. t på et gitt punkt. I figur 4 er punktet oransje og tangentlinjen er grønn. Den øyeblikkelige hastigheten på det punktet er skråningen til den linjen.
Hastighet er definert som den absolutte verdien eller hastighetsmodulen og er alltid positiv (skilt, veier og motorveier er alltid positive, aldri negative). Uttrykkene "hastighet" og "hastighet" kan brukes om hverandre hver dag, men i fysikk er skillet mellom vektor og skalar nødvendig.
v = ΙvΙ = v
Hastigheten kan endres i løpet av bevegelsen, og virkeligheten er at det forventes å gjøre det. Det er en størrelse som kvantifiserer denne endringen: akselerasjon. Hvis vi bemerker at hastighet er endring i posisjon med hensyn til tid, er akselerasjon endring i hastighet med hensyn til tid.
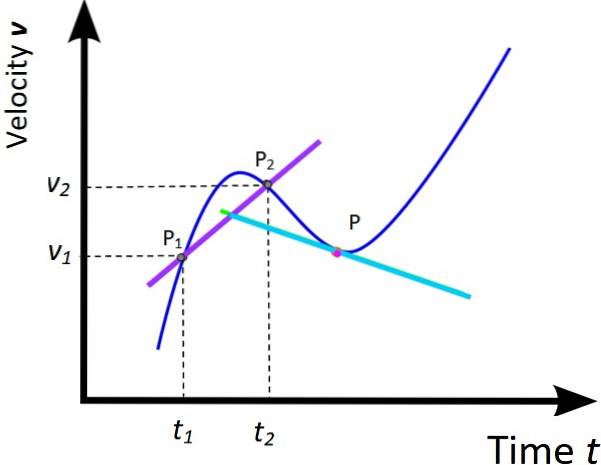
Behandlingen gitt til grafen for x vs. t av de to foregående seksjonene kan utvides til den tilsvarende grafen for v vs. t. Følgelig er en gjennomsnittlig akselerasjon og en øyeblikkelig akselerasjon definert som:
tilm = (vto - v1) / (tto -t1) = Δv / Δt (Helling av den lilla linjen)
I en-dimensjonal bevegelse har vektorer etter konvensjon positive eller negative tegn, avhengig av om de går den ene eller den andre. Når akselerasjon har samme retning som hastighet, øker den størrelsen, men når den har motsatt retning og hastigheten reduseres. Det sies da at bevegelsen er forsinket.
Klassifiseringen av rettlinjede bevegelser er generelt basert på:
- Om akselerasjonen er konstant eller ikke.
- Bevegelse går langs en horisontal eller vertikal linje.
Når akselerasjonen er konstant, er den gjennomsnittlige akselerasjonen tilm tilsvarer øyeblikkelig akselerasjon til og det er to alternativer:
- At akselerasjonen er lik 0, i hvilket tilfelle hastigheten er konstant og det er en enhetlig rettlinjet bevegelse eller MRU.
- Annen konstant akselerasjon enn 0, hvor hastigheten øker eller avtar lineært med tiden (Uniformly Varied Rectilinear Motion eller MRUV):
Hvor vF Y tF er henholdsvis endelig hastighet og tid, og veller Y teller de er starthastighet og tid. Ja teller = 0, For å løse den endelige hastigheten har vi den allerede kjente ligningen for den endelige hastigheten:
vF = veller + på
Følgende ligninger er også gyldige for denne bevegelsen:
- Posisjon som en funksjon av tid: x = xeller + veller .t + ½ klto
- Hastighet som en funksjon av posisjon: vFto = vellerto + 2..Δx (Med Δx = x - xeller)
Horisontale bevegelser er de som foregår langs den horisontale aksen eller x-aksen, mens vertikale bevegelser gjør det langs y-aksen. Vertikale bevegelser under tyngdekraften er de hyppigste og mest interessante.
I de forrige ligningene tar vi a = g = 9,8 m / sto rettet vertikalt nedover, en retning som nesten alltid velges med et negativt tegn.
På denne måten, vF = veller + på Det forvandler seg inn vF = veller - gt og hvis starthastigheten er 0 fordi objektet ble droppet fritt, forenkler det ytterligere til vF = - gt. Så lenge det ikke tas hensyn til luftmotstand, selvfølgelig.
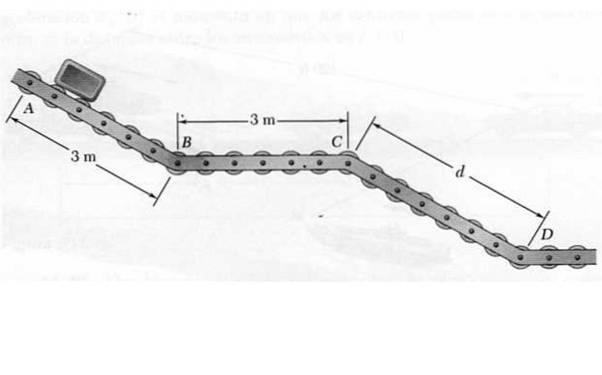
Ved punkt A frigjøres en liten pakke for å bevege seg langs transportøren med glideskiver ABCD vist på figuren. Mens du går ned bakkene AB og CD, har pakken en konstant akselerasjon på 4,8 m / sto, mens i den horisontale delen BC holder konstant hastighet.
Å vite at hastigheten som pakken kommer til D er 7,2 m / s, bestemme:
a) Avstanden mellom C og D..
b) Tiden det tar for pakken å komme til slutten.
Bevegelsen av pakken utføres i de tre rettlinjede seksjonene som er vist, og for å beregne det som kreves, kreves hastigheten ved punktene B, C og D. La oss analysere hver seksjon separat:
Siden tiden ikke er tilgjengelig i denne delen, vil den brukes vFto = vellerto + 2..Δx med vo = 0:
vFto = 2a.Δx → vFto= 2. 4,8 m / sto . 3 m = 28,8 mto/ sto → vF = 5,37 m / s = vB
Tiden det tar pakken å reise seksjonen AB er:
tAB = (vF - veller) / a = 5,37 m / s / 4,8 m / sto = 1,19 s
Hastigheten i seksjon BC er derfor konstant vB = vC = 5,37 m / s. Tiden det tar for pakken å reise denne delen er:
tF.Kr. = avstand F.Kr. / vB = 3 m / 5,37 m / s = 0,56 s
Starthastigheten til denne seksjonen er vC = 5,37 m / s, den endelige hastigheten er vD = 7,2 m / s, ved vDto = vCto + 2. a. d verdien av blir ryddet d:
d = (vDto - vCto) /2.a = (7.2to - 5.37to)/to x 4,8 m = 2,4 m
Tiden beregnes som:
tCD = (vD - vC) / a = (7,2 - 5,37) / 4,8 s = 0,38 s.
Svarene på spørsmålene er:
a) d = 2,4 m
b) Reisetiden er tAB + tF.Kr. + tCD = 1,19 s +0,56 s +0,38 s = 2,13 s.
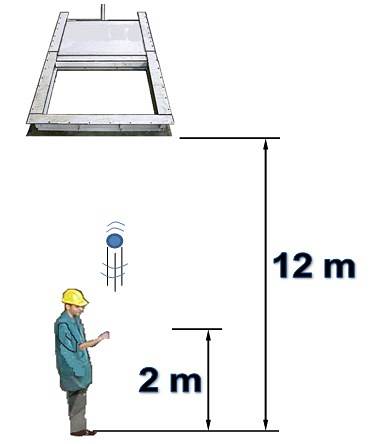
En person er under en horisontal port som opprinnelig er åpen og 12 m høy. Personen kaster en gjenstand vertikalt mot porten med en hastighet på 15 m / s.
Det er kjent at porten lukkes 1,5 sekunder etter at personen har kastet gjenstanden fra en høyde på 2 meter. Luftmotstand vil ikke bli tatt i betraktning. Svar på følgende spørsmål, begrunn:
a) Kan objektet passere gjennom porten før den lukkes?
b) Vil objektet noen gang kollidere med den lukkede porten? Hvis ja, når gjør det?
Det er 10 meter mellom startposisjonen til ballen og porten. Det er et vertikalt kast oppover, hvor denne retningen blir tatt som positiv.
Du kan finne ut hastigheten det tar å nå denne høyden, med dette resultatet beregnes tiden det tar å gjøre det og sammenlignes med lukketiden til porten, som er 1,5 sekunder:
vF to= veller to- 2 g. Δog → vF = (15to - to x 9.8 x10)1/2 m = 5,39 m / s
t = (vF - veller) / g = (5,39 - 15) / (-9,8) s = 0,98 s
Siden denne tiden er mindre enn 1,5 sekunder, konkluderes det med at objektet kan passere gjennom porten minst en gang.
Vi vet allerede at objektet klarer å passere gjennom porten mens du går opp, la oss se om det gir det en sjanse til å passere igjen når du går ned. Hastigheten, når den når portens høyde, har samme styrke som når den går oppover, men i motsatt retning. Derfor jobber vi med -5,39 m / s, og tiden det tar å nå denne situasjonen er:
t = (vF - veller) / g = (-5,39 - 15) / (-9,8) s = 2,08 s
Siden porten forblir åpen i bare 1,5 s, er det tydelig at den ikke har tid til å passere igjen før den lukkes, siden den finner den stengt. Svaret er: objektet hvis det kolliderer med den lukkede luken etter 2,08 sekunder etter at den er kastet, når den allerede er synkende.
Ingen har kommentert denne artikkelen ennå.