
Parallelogrammetodeeksempler, løste øvelser
De parallellogrammetode er en grafisk metode for å legge til to vektorer i planet. Det brukes ofte for å finne resultatet av to krefter påført et legeme eller med to hastigheter, som i tilfelle en svømmer som har til hensikt å krysse en elv vinkelrett og blir avbøyd av strømmen.
For å konstruere parallellogrammet, må opprinnelsen til vektorene som skal legges til, tegnet i målestokk, falle sammen på et punkt.
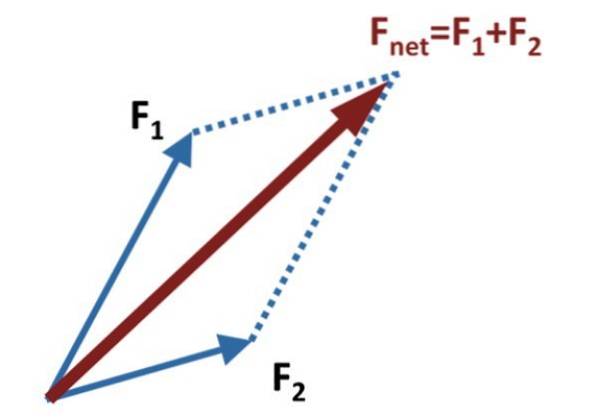
Deretter tegnes hjelpelinjer parallelt med hver vektor, og når enden til den andre, som vist i figuren ovenfor.
Summen eller den resulterende vektoren, også kalt nettokraften, er vektoren Fnett, som er oppnådd ved å tegne vektoren som kommer fra den felles opprinnelsen til F1 Y Fto, til det punktet hvor de parallelle hjelpelinjene krysser hverandre. I diagrammet til figuren er disse representert med stiplede linjer.
Metoden får navnet sitt fra figuren som dannes med tilleggsvektorene og hjelpelinjene, som nettopp er et parallellogram. Hoveddiagonalen til parallellogrammet er sumvektoren.
Det er veldig viktig å merke seg at rekkefølgen i tilleggsvektorene er plassert ikke endrer summen i det hele tatt, siden denne operasjonen mellom vektorene er kommutativ.
Artikkelindeks
- 1 Eksempel på parallellogrammetoden trinnvis
- 1.1 Spesielt tilfelle: summen av vinkelrette vektorer
- 2 Løst øvelser
- 2.1 - Øvelse 1
- 2.2 - Øvelse 2
- 3 Referanser
Eksempel på parallellogrammetoden trinn for trinn
Følgende bilde viser vektorene v Y eller i vilkårlige enheter. Vektoren v måler 3,61 enheter og danner en vinkel på 56,3º med horisontal, mens eller måler 6,32 enheter og en vinkel på 18,4 ° i forhold til referanselinjen.
Vi skal finne vektorsummen ved hjelp av parallellogrammetoden.
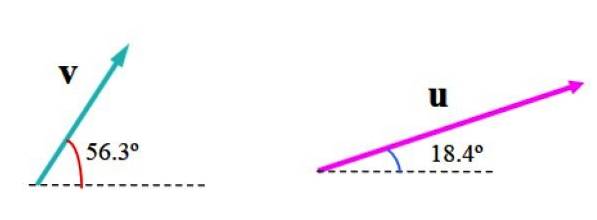
Velg en passende skala, slik som den som er vist i følgende figur, der flyet er delt av et rutenett. Bredden på firkanten representerer en (1) enhet.
Siden vektorene ikke endres når de oversettes, er de plassert på en slik måte at deres opprinnelse sammenfaller med opprinnelsen til koordinatsystemet (bildet til venstre).
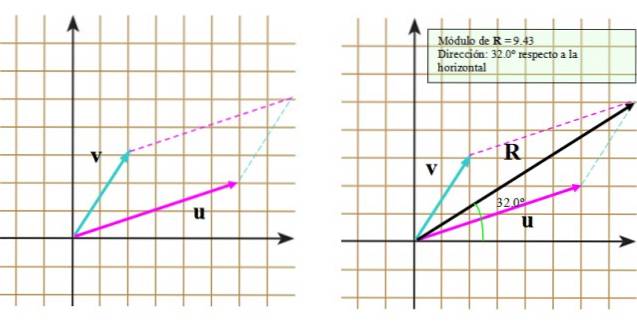
La oss nå følge disse trinnene:
- Plott etter slutten av vektoren v en segmentert linje som er parallell med vektoren eller.
- Gjenta prosedyren, men denne gangen med slutten av vektoren eller.
- Tegn hoveddiagonalen som strekker seg fra den felles opprinnelsen til skjæringspunktet for de segmenterte linjene.
Resultatet kan sees i riktig bilde, der den resulterende vektoren vises R.
Hvis vi vil vite størrelsen på R, vi kan måle lengden og sammenligne den med skalaen vi har. Og når det gjelder retning, kan den horisontale aksen eller den vertikale aksen brukes som referanser, for eksempel.
Når du bruker den horisontale aksen eller x-aksen, vil vinkelen som R form med nevnte akse måles med vinkelmåler og på denne måten vet vi retningen av R.
Likeledes størrelsen og retningen av R kan beregnes ved hjelp av cosinus- og sinussetningene, siden parallellogrammet som dannes kan deles i to kongruente trekanter, hvis sider er modulene til vektorene eller, v Y R. Se utarbeidet eksempel 1.
Spesielt tilfelle: summen av vinkelrette vektorer
Når vektorene er vinkelrett på hverandre, er figuren som dannes et rektangel. Modulen til den resulterende vektoren tilsvarer lengden på diagonalen, som enkelt kan beregnes ved hjelp av Pythagoras teorem.
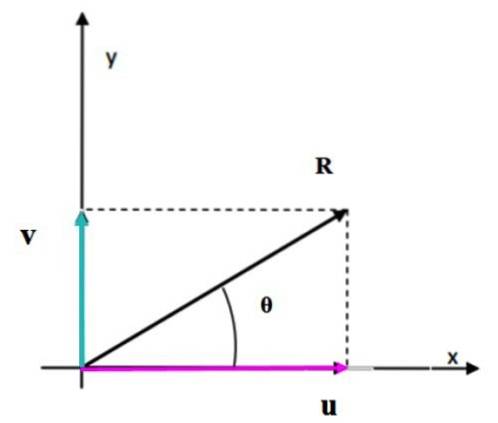
Løst øvelser
- Øvelse 1
Vi har vektoren v, som måler 3,61 enheter og danner en vinkel på 56,3º med horisontal og vektor eller, hvis mål er 6,32 enheter og danner en vinkel på 18,4º (figur 2). Bestem modulen til den resulterende vektoren R = eller + v og retningen som vektoren danner med den horisontale aksen.
Løsning
Parallellogrammetoden brukes i henhold til trinnene beskrevet ovenfor for å oppnå vektoren R. Som sagt før, hvis vektorene er nøye tegnet ved å følge skalaen og bruke linjalen og vinkelmåleren, vil størrelsen og retningen av R måles direkte på tegningen.
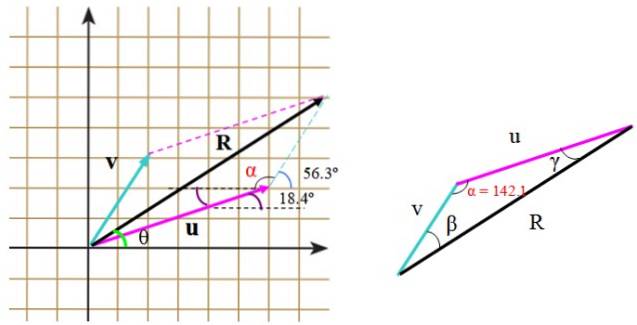
De kan også beregnes direkte, ved hjelp av trigonometri og egenskapene til vinkler. Når trekanten som er dannet ikke er riktig, som i dette tilfellet, blir kosinosetningen brukt for å finne den manglende siden.
I trekanten til høyre måler sidene u, v og R. For å bruke kosinosetningen er det nødvendig å kjenne vinkelen mellom v Y eller, som vi kan finne ved hjelp av rutenettet, ved å plassere vinklene på riktig måte.
Denne vinkelen er α og består av:
α = (90-56,3 º) + 90 º + 18,4 º = 142,1 º
I følge kosinussetningen:
Rto = vto + ellerto - 2u⋅v⋅cos α = 3,61to + 6.32to - 2 × 3,61 × 6,32 × cos 142,1º = 88,98
R = 9,43 enheter.
Til slutt, vinkelen mellom R og den horisontale aksen er θ = 18,4 º + γ. Vinkelen γ finner du ved hjelp av sinussetningen:
sin α / R = sin γ / u
Derfor:
sin γ = v (sin α / R) = 3,61 x (sin 142,1º / 9,43)
γ = 13,6º
θ = 18,4 º + 13,6 º = 32 º
- Øvelse 2
En svømmer er i ferd med å krysse en elv som svømmer vinkelrett på strømmen med en konstant hastighet på 2,0 m / s. Svømmeren starter fra A, men havner ved B, et punkt nedstrøms, på grunn av strømmen som avledet ham.
Hvis strømens hastighet er 0,8 m / s og alle hastigheter antas konstant, finn svømmerens hastighet sett av en observatør som står på kysten.
Løsning
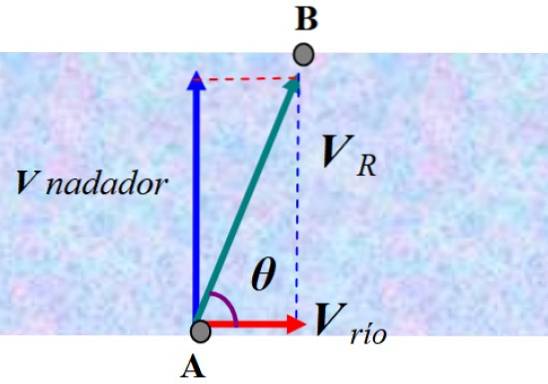
En observatør som står på kysten vil se hvordan svømmeren avbøyes i henhold til den resulterende hastigheten VR. For å finne svaret, må vi legge vekt på svømmerens hastighet i forhold til vannet og strømens hastighet, som vi kaller V Elv:
V R = V svømmer + V Elv
I figuren, som ikke skaleres, ble vektorene lagt til for å oppnå V R. I dette tilfellet kan Pythagoras teorem brukes for å oppnå størrelsen:
VRto = 2,0to + 0,8to = 4,64
VR = 2,15 m / s
Retningen svømmeren avviker fra den vinkelrette retningen beregnes enkelt, og bemerker at:
θ = arctg (2 / 0,8) = 68,2º
Så avviker svømmeren 90º - 68,2º = 27,2º fra sin opprinnelige retning.
Referanser
- Bauer, W. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysikk. 2. plass. Ed. McGraw Hill.
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 1.


Ingen har kommentert denne artikkelen ennå.