
Trachtenberg-metoden hva den består av, eksempler
De Trachtenberg-metoden er et system for å utføre aritmetiske operasjoner, hovedsakelig multiplikasjon, på en enkel og rask måte, når reglene er kjent og mestret.
Det ble utviklet av den russiskfødte ingeniøren Jakow Trachtenberg (1888-1953) da han var fange av nazistene i en konsentrasjonsleir, som en form for distraksjon for å opprettholde sunn fornuft mens han fortsatte i fangenskap..
Artikkelindeks
- 1 Hva den består av, fordeler og ulemper
- 2 Eksempler
- 2.1 - Multipliser et tall med 10 eller med 11
- 2.2 - Multiplikasjon med tall fra 12 til 19
- 2.3 - Utvidelse av reglene for multiplikasjon med 13,… opp til 19
- 3 regler for produkter etter 6, 7 og 5
- 3.1 - Multiplikasjon med 6
- 3.2 - Multiplikasjon med 7
- 3.3 - Multiplikasjon med 5
- 4 Regler for produkter innen 9
- 5 Multiplikasjon med 8, 4, 3 og 2
- 5.1 - Multiplikasjon med 8
- 5.2 - Multiplikasjon med 4
- 5.3 - Multiplikasjon med 3
- 5.4 - Multiplikasjon med 2
- 6 Multipliser med sammensatte figurer
- 6.1 Trening
- 7 Referanser
Hva den består av, fordeler og ulemper
Fordelen med denne metoden er at for å utføre multiplikasjon er det ikke nødvendig å huske multiplikasjonstabellene, i det minste delvis, er det bare nok å vite hvordan man teller og legger til, samt å dele et siffer med to.
Ulempen er at det ikke er noen universell regel for å multiplisere med noe tall, snarere regelen varierer i henhold til multiplikatoren. Imidlertid er mønstrene ikke vanskelig å huske, og tillater i prinsippet operasjoner uten hjelp av papir og blyant..
Gjennom denne artikkelen vil vi fokusere på reglene for å multiplisere raskt.
Eksempler
For å anvende metoden er det nødvendig å kjenne reglene, det er derfor vi skal presentere dem en etter en og med eksempler:
- Multipliser et tall med 10 eller med 11
Regel for å multiplisere med 10
-Hvis du vil multiplisere et tall med 10, legger du bare til null til høyre. For eksempel: 52 x 10 = 520.
Regler for å multiplisere med 11
-Et null legges til begynnelsen og slutten av figuren.
-Hvert siffer legges til med naboen til høyre, og resultatet plasseres under det tilsvarende sifferet i den opprinnelige figuren.
-Hvis resultatet overstiger ni, blir enheten notert og en prikk plasseres på den for å huske at vi har en enhet som vil bli lagt til i summen av neste figur med naboen til høyre.
Detaljert eksempel på multiplikasjon med 11
Multipliser 673179 med 11
06731790 x 11 =
--
= 7404969
Trinnene som kreves for å nå dette resultatet, illustrert med farger, er som følger:
-1 av enheten til multiplikatoren (11) ble multiplisert med 9 av multiplikatoren (06731790) og 0 ble lagt til den. Enhetstallet for resultatet ble oppnådd: 9.
-Deretter multipliserer vi 1 med 7 og legger til ni til 16, og vi bærer 1, vi plasserer ti-tallet: 6.
-Etter å ha multiplisert 1 med 1, gir han nabo til høyre 7 pluss 1 som han bar 9 for hundre.
-Neste figur er oppnådd ved å multiplisere 1 med 3 pluss naboen 1, det er 4 for tusenvis.
-Multipliser 1 med 7 og legg til naboen 3, noe som resulterer i 10, plasser null (0) som et ti tusen siffer og tar ett.
-Deretter 1 ganger 6 pluss nabo 7 resultater 13 pluss en 1 som hadde resultater 14, den 4 som hundretusen siffer og tar 1.
-Til slutt multipliseres 1 med null som ble lagt til i begynnelsen, noe som gir null pluss naboen 6 pluss en som ble båret. Det viser seg endelig 7 for tallet som tilsvarer millionene.
- Multiplikasjon med tall fra 12 til 19
Slik multipliserer du et tall med 12:
-Et null legges til i begynnelsen og et annet null på slutten av figuren som skal multipliseres.
-Hvert siffer i figuren som skal multipliseres blir doblet og lagt til med naboen til høyre.
-Hvis summen overstiger 10, blir en enhet lagt til neste dupliseringsoperasjon og summen med naboen.
Eksempel på multiplikasjon med 12
Multipliser 63247 med 12
0632470 x 12 =
-
758964
Detaljene for å komme til dette resultatet, strengt etter de angitte reglene, er vist i følgende figur:

- Utvidelse av reglene for multiplikasjon med 13, ... opp til 19
Metoden med å multiplisere med 12 kan utvides til å bli multiplisert med 13, 14 til 19 ved å endre regelen om dobling ved å tredoble for tilfellet tretten, firdoble for tilfelle av 14 og så videre til den når 19.
Regler for produkter etter 6, 7 og 5
- Multiplikasjon med 6
-Legg til nuller i begynnelsen og slutten av figuren for å multiplisere med 6.
-Legg til halvparten av naboen til høyre for hvert siffer, men hvis sifferet er merkelig, legg til 5 i tillegg.
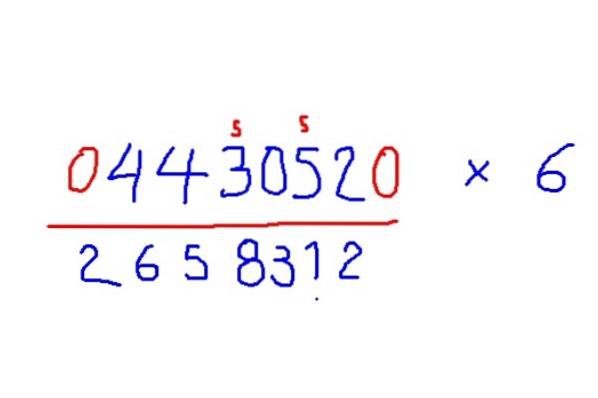
- Multiplikasjon med 7
-Legg til nuller til begynnelsen og slutten av tallet som skal multipliseres.
-Dobbelt hvert siffer og legg til den nedre hele halvdelen av naboen, men hvis sifferet er merkelig, legg til 5.
Eksempel på multiplikasjon med 7
-Multipliser 3412 med 7
-Resultatet er 23884. For å bruke reglene, anbefales det å først gjenkjenne oddetallene og plassere en liten 5 over dem for å huske å legge til denne figuren i resultatet..
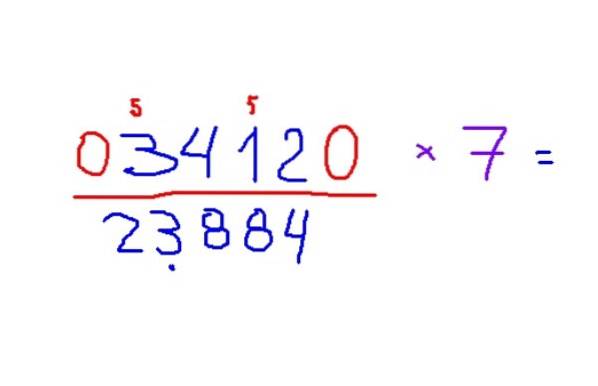
- Multiplikasjon med 5
-Legg til nuller til begynnelsen og slutten av tallet som skal multipliseres.
-Plasser den nedre hele halvdelen av naboen under hvert siffer til høyre, men hvis sifferet er merkelig, legg til i tillegg 5.
Eksempel multipliser med 5
Multipliser 256413 med 5
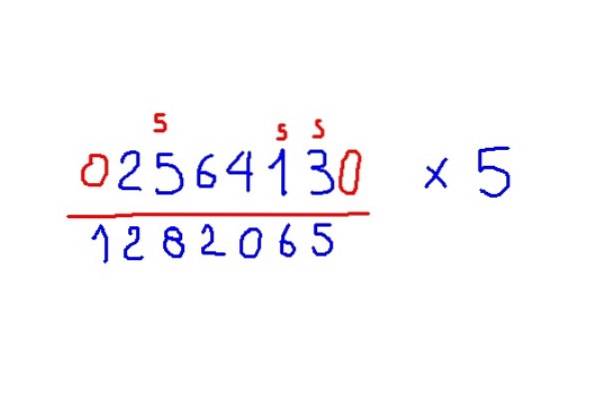
Regler for produkter innen 9
-Et null legges til i begynnelsen og et annet på slutten av figuren som skal multipliseres med ni.
-Det første sifferet til høyre oppnås ved å trekke det tilsvarende sifferet i tallet for å multiplisere fra 10.
-Deretter trekkes neste siffer fra 9 og naboen legges til.
-Det forrige trinnet gjentas til vi når nullpunktet til multiplikatoren, der vi trekker 1 fra naboen og resultatet kopieres til under null..
Eksempel på multiplikasjon med 9
Multipliser 8769 med 9:
087690 x 9 =
--
78921
Operasjoner
10 - 9 = 1
(9-6) + 9 = 1to (de to og tar 1)
(9-7) + 1 + 6 =9
(9-8) +7 =8
(8-1) = 7
Multiplikasjon med 8, 4, 3 og 2
-Legg til nuller til begynnelsen og slutten av tallet som skal multipliseres.
-For det første sifferet fra høyre trekker du fra 10 og resultatet blir doblet.
-For de følgende sifrene trekker vi fra 9, dobles resultatet og naboen legges til.
-Når du når null, trekker du 2 fra naboen til høyre.
- Multiplikasjon med 8
Eksempel på multiplikasjon med 8
-Multipliser 789 med 8
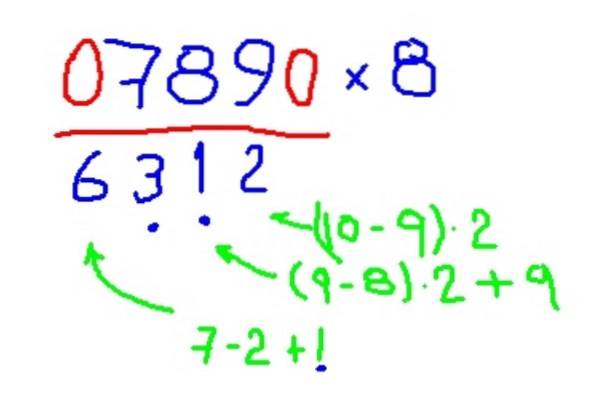
- Multiplikasjon med 4
-Legg til nuller til høyre og venstre for multiplikatoren.
-Trekk det tilsvarende sifferet fra enheten ved å legge til 5 hvis det er et oddetall.
-Trekk hvert siffer i multiplikasjonen fra 9 i skjemaet, legg halvparten av naboen til høyre, og hvis det er et oddetall, legg til 5 i tillegg.
-Når du når nullpunktet for begynnelsen av multiplikatoren, plasser halvparten av naboen minus en.
Eksempel på multiplikasjon med 4
Multipliser 365187 x 4
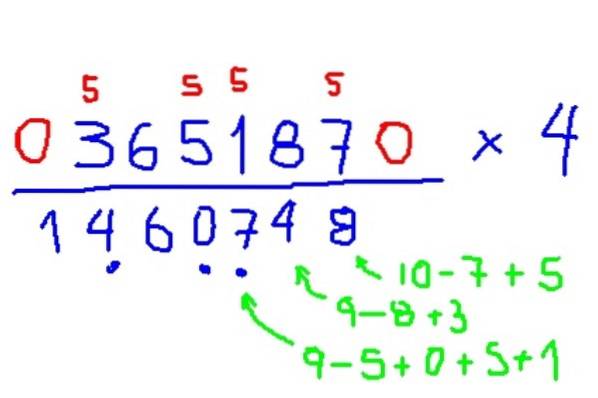
- Multiplikasjon med 3
-Legg til null i hver ende av multiplikatoren.
-Trekk 10 minus ensifret, og legg til 5 hvis det er et oddetall.
-For de andre sifrene trekker du 9, dobler du resultatet, legger til halvparten av naboen og legger til 5 hvis det er rart..
-Når du når nullpunktet for overskriften, plasserer du den nedre heltallshalvdelen av naboen minus 2.
Eksempel på multiplikasjon med 3
Multipliser 2588 med 3

- Multiplikasjon med 2
-Legg til nuller i endene og doble hvert siffer, hvis det overstiger 10, legg til ett til det neste.
Eksempel multipliser med 2
Multipliser 2374 med 2
023740 x 2
04748
Multipliser med sammensatte figurer
Reglene oppført ovenfor gjelder, men resultatene kjøres til venstre av antall steder som tilsvarer tiere, hundrevis og så videre. La oss se på følgende eksempel:
Trening
Multipliser 37654 med 498
0376540 x 498
301232 linjal for 8
338886-regel for 9
150616 linjal for 4
18751692 endelig sum
Referanser
- Cutler, Ann. 1960 Trachtenbergs hastighetssystem for grunnleggende matematikk. Doubleday & CO, NY.
- Dialnet. Rask grunnleggende matte system. Gjenopprettet fra: dialnet.com
- Matematisk hjørne. Rask multiplikasjon etter Trachtenberg-metoden. Gjenopprettet fra: rinconmatematico.com
- Trachtenberg Speed System of Basic Mathematics. Gjenopprettet fra: trachtenbergspeedmath.com
- Wikipedia. Trachtenberg-metoden. Gjenopprettet fra: wikipedia.com


Ingen har kommentert denne artikkelen ennå.