Konjugere interne og eksterne vinkler eksempler, øvelser

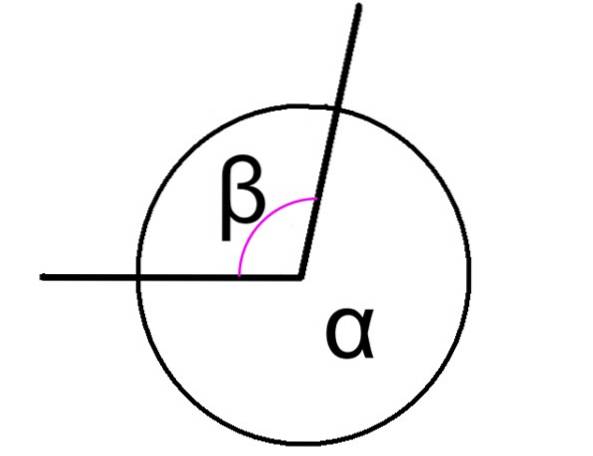
De konjugerte vinkler Det er de som, når de er lagt til, gir 360 ° som et resultat, uavhengig av om disse vinklene er tilstøtende eller ikke. I figur 1 er to konjugerte vinkler vist, betegnet som α og β.

I dette tilfellet har vinklene α og β i figuren et felles toppunkt, og sidene deres er vanlige, derfor er de tilstøtende. Forholdet mellom dem uttrykkes som følger:

α + β = 360º

Det er en klassifisering av vinklene etter summen. Andre viktige definisjoner inkluderer komplementære vinkler, hvis sum er 90 º og tilleggsvinkler, totalt 180 º.

På den annen side, la oss nå se på to parallelle linjer kuttet av en sekant, hvis arrangement er vist nedenfor:

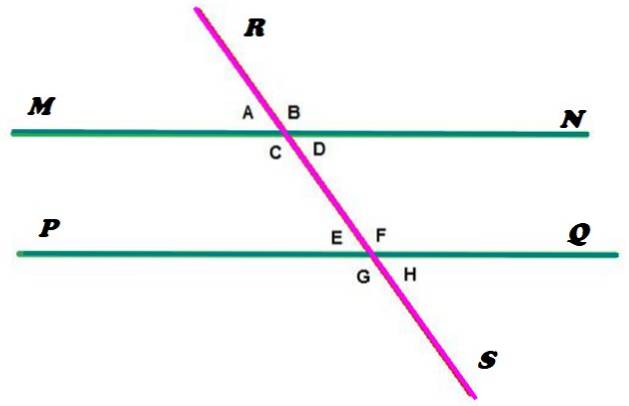
Linjene MN og PQ er parallelle, mens linjen RS er sekant og krysser parallellene på to punkter. Som man kan se, bestemmer denne konfigurasjonen dannelsen av åtte vinkler, som er betegnet med små bokstaver.

I følge definisjonen gitt i begynnelsen er vinklene a, b, c og d konjugert. Og på samme måte er e, f, g og h, siden begge tilfeller er sanne:

a + b + c + d = 360º

Y

e + f + g + h = 360º

For denne konfigurasjonen er to vinkler konjugert hvis de er på samme side i forhold til sekantlinjen RS og begge er interne eller eksterne. I det første tilfellet snakker vi om vinkler indre konjugater, mens i det andre er de vinkler eksterne konjugater.

Artikkelindeks

• 1 Eksempler
• 2 Innvendige vinkler på en firkant
  • 2.1 Eksempler
• 3 Øvelser
  • 3.1 - Øvelse 1
  • 3.2 - Øvelse 2
• 4 Referanser

Eksempler

I figur 2 er de ytre vinklene de som er utenfor regionen avgrenset av linjene MN og PQ, de er vinklene A, B, G og H. Mens vinklene som ligger mellom de to linjene er C, D, E og F.

Nå er det nødvendig å analysere hvilke vinkler som er til venstre og hvilke til høyre for sekanten.

Til venstre for RS er vinklene A, C, E og G. Og til høyre er vinklene B, D, F og H.

Vi fortsetter umiddelbart med å bestemme de konjugerte vinkelparene, i henhold til definisjonen gitt i forrige avsnitt:

-A og G, ekstern og til venstre for RS.

-D og F, internt og til høyre for RS.

-B og H, utvendig og til høyre for RS.

-C og E, internt og til venstre for RS.

Egenskap av konjugerte vinkler mellom parallelle linjer

De konjugerte vinklene mellom parallelle linjer er supplerende, det vil si at summen er lik 180º. På denne måten gjelder følgende for figur 2:

A + G = 180º

D + F = 180º

B + H = 180º

C + E = 180º

Parene med tilsvarende vinkler for parallelle linjer

De er de som er på samme side av sekantlinjen, de er ikke tilstøtende og den ene er intern og den andre er ekstern. Det er viktig å visualisere dem, siden deres mål er det samme, fordi de er motsatte vinkler ved toppunktet.

Når vi kommer tilbake til figur 2, er de tilsvarende vinkelparene identifisert som:

-A og E

-C og G

-B og F

-D og H

Innvendige vinkler på en firkant

Kvadrilaterale er 4-sidige polygoner, blant annet firkanten, rektangelet, trapesformet, parallellogrammet og romben, for eksempel. Uansett form, i noen av dem er det sant at summen av deres indre vinkler er 360 °, derfor oppfyller de definisjonen gitt i begynnelsen..

La oss se noen eksempler på firkanter og hvordan man beregner verdien av deres indre vinkler i henhold til informasjonen i de foregående avsnittene:

Eksempler

a) Tre av vinklene til et firkantmål 75º, 110º og 70º. Hvor mye skal den gjenværende vinkelen måle?

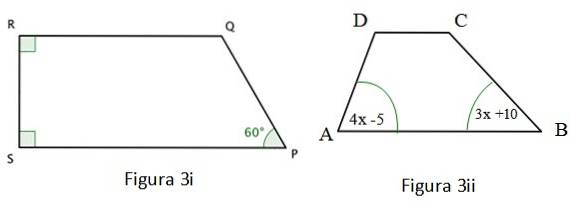
b) Finn verdien av vinkelen ∠Q i figur 3 i.

c) Beregn mål på vinkelen ∠A i figur 3 ii.

Løsning til

La α være den manglende vinkelen, det er tilfreds med at:

α + 75º + 110º + 70º = 360º → α = 105º

Løsning b

Figur 3i vist er a trapes og to av dens indre vinkler er rette, som er merket med en farget firkant i hjørnene. For dette firsidet er følgende bekreftet:

∠R + ∠S + ∠P + ∠Q = 360º; ∠S = ∠R = 90 °; ∠P = 60º

Derfor:

∠ Q = 2 x 90º + 60º = 240º

Løsning c

Kvadrilateralen i figur 3 ii er også en trapesform, som følgende gjelder:

∠A + ∠B + ∠C + ∠D = 360º

Derfor:

4x -5 + 3x + 10 +180 = 360

7x + 5 = 180

x = (180 - 5) / 7

x = 25

For å bestemme vinkelen som er bedt om i uttalelsen, bruker vi at ∠A = 4x - 5. Ved å erstatte den tidligere beregnede verdien av x følger det at ∠A = (4 × 25) -5 = 95º

Opplæring

- Øvelse 1

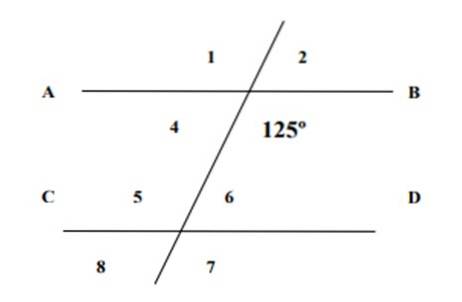
Å vite at en av de viste vinklene er 125º, finn målingene til de 7 gjenværende vinklene i følgende figur og rettferdiggjør svarene.

Løsning

Vinkel 6 og vinkel 125º er indre konjugater, hvis sum er 180º, i henhold til egenskapen til konjugerte vinkler, derfor:

∠6 + 125º = 180º → ∠6 = 180º - 125º = 55º

På den annen side er ∠6 og ∠8 motsatte vinkler ved toppunktet, hvis mål er det samme. Derfor måler ∠8 55º.

Vinkelen ∠1 er også motsatt av toppunktet ved 125 º, så kan vi bekrefte at ∠1 = 125 º. Vi kan også appellere til at de tilsvarende vinkelparene har samme mål. I figuren er disse vinklene:

∠7 = 125 º

∠2 = ∠6 = 55 º

∠1 = ∠5 = 125º

∠4 = ∠8 = 55 º

- Øvelse 2

Finn verdien av x i følgende figur og verdiene til alle vinklene:

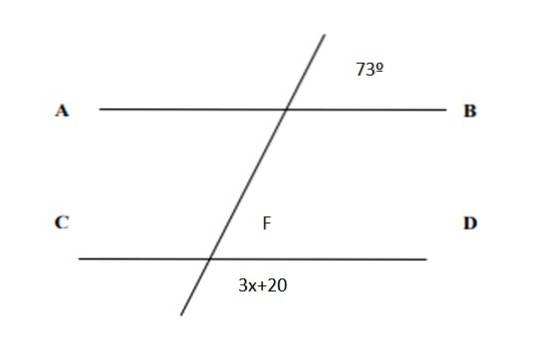
Løsning

Siden de er tilsvarende par, følger det at F = 73º. Og på den annen side er summen av de konjugerte parene 180º, derfor:

3x + 20º + 73º = 180º

3x = 180º - 73º -20º = 87

Endelig er verdien av x:

x = 87/3 = 29

Når det gjelder alle vinklene, er de oppført i følgende figur:

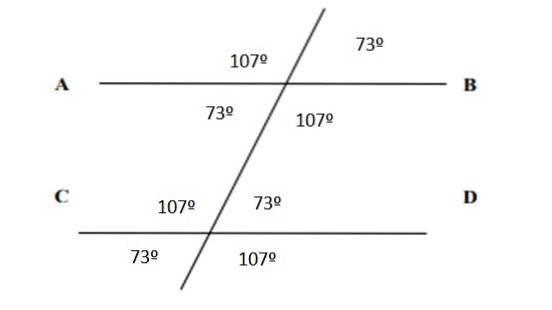
Referanser

1. Vinkelgrupper. Utfyllende, supplerende og utfyllende vinkler Forklaring. Gjenopprettet fra: thisiget.com/
2. Baldor, A. 1983. Plane and Space Geometry and Trigonometry. Patria Cultural Group.
3. Corral, M. Mathematics LibreTexts: Angles. Gjenopprettet fra: math.libretexts.org.
4. Mathmania. Klassifisering og konstruering av vinkler etter måling. Gjenopprettet fra: mathematania.com/
5. Wentworth, G. Plane Geometry. Gjenopprettet fra: gutenberg.org.
6. Wikipedia. Konjugerte vinkler. Gjenopprettet fra: es.wikipedia.org.