
Komplekse tallegenskaper, eksempler, operasjoner
De komplekse tall er det numeriske settet som inkluderer reelle tall og alle røttene til polynomene, inkludert de jevne røttene til de negative tallene. Disse røttene eksisterer ikke i settet med reelle tall, men i komplekse tall er det løsningen.
Et komplekst tall består av en reell del og en del kalt “imaginær”. Den virkelige delen heter til, for eksempel, og den imaginære delen ib, med til Y b reelle tall og "i" liker imaginær enhet. På denne måten tar det komplekse tallet form:
z = a + ib

Eksempler på komplekse tall er 2 - 3i, -πi, 1 + (1/2) i. Men før vi opererer med dem, la oss se hvor den imaginære enheten har sin opprinnelse Jeg, vurderer denne kvadratiske ligningen:
xto - 10x + 34 = 0
I hvilke a = 1, b = -10 og c = 34.
Når vi bruker løsningsformelen for å bestemme løsningen, finner vi følgende:

Hvordan bestemme verdien av √-36? Det er ikke noe reelt tall som kvadreres, og resulterer i en negativ mengde. Deretter konkluderes det med at denne ligningen ikke har noen reelle løsninger.
Imidlertid kan vi skrive dette:
√-36 = √-6to = √6to (-1) = 6√-1
Hvis vi definerer en viss verdi x slik at:
xto = -1
Deretter:
x = ± √-1
Og ligningen ovenfor ville ha en løsning. Derfor ble den imaginære enheten definert som:
i = √-1
Og så:
√-36 = 6i
Mange antikkens matematikere arbeidet med å løse lignende problemer, særlig renessansen Girolamo Cardano (1501-1576), Nicolo Fontana (1501-1557) og Raffaele Bombelli (1526-1572).
Flere år senere kalte René Descartes (1596-1650) mengder som √-36 i eksemplet "imaginær". Av denne grunn er √-1 kjent som imaginær enhet.
Artikkelindeks
- 1 Egenskaper for komplekse tall
- 2 Representasjon av komplekse tall
- 2.1 - Binomial form
- 2.2 - Polarform
- 3 Eksempler på komplekse tall
- 4 Hva er de for??
- 5 Operasjoner med komplekse tall
- 5.1 - Eksempel 1
- 5.2 - Eksempel 2
- 6 Søknad
- 7 Referanser
Egenskaper for komplekse tall
-Settet med komplekse tall er betegnet C og inkluderer de reelle tallene R og de imaginære tallene Im. Antall sett er representert i et Venn-diagram, som vist i følgende figur:
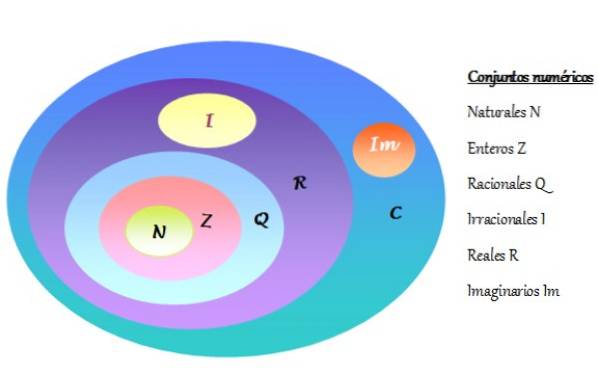
-Hvert komplekst tall består av en reell del og en imaginær del.
-Når den imaginære delen av et komplekst tall er 0, er det et rent reelt tall.
-Hvis den virkelige delen av et komplekst tall er 0, er tallet rent imaginært.
-To komplekse tall er like hvis deres respektive virkelige del og imaginære del er de samme.
-Med komplekse tall utføres de kjente operasjonene av addisjon, subtraksjon, multiplikasjon, produkt og forbedring, noe som resulterer i et annet komplekst tall.
Representasjon av komplekse tall
Komplekse tall kan vises på forskjellige måter. Her er de viktigste:
- Binomial form
Det er skjemaet som ble gitt i begynnelsen, hvor z er det komplekse tallet, til det er den virkelige delen, b er den imaginære delen e Jeg er den tenkte enheten:
z = a + ib
Eller også:
z = x + iy
En måte å tegne det komplekse tallet på er gjennom det komplekse planet vist i denne figuren. Den imaginære aksen Im er vertikal, mens den virkelige aksen er horisontal og betegnes som Re.
Det komplekse tallet z er representert på dette planet som et koordinatpunkt (x, y) eller (a, b), slik det gjøres med punktene i det virkelige planet.
Avstanden fra opprinnelsen til punktet z er modulet til det komplekse tallet, betegnet som r, mens φ er vinkelen som dannes r med den virkelige aksen.
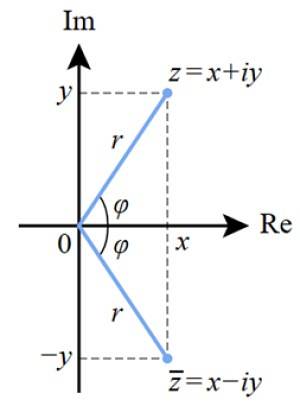
Denne representasjonen er nært beslektet med vektorene i det virkelige planet. Verdien av r tilsvarer modul av det komplekse tallet.
- Polarform
Polarformen består i å uttrykke det komplekse tallet ved å gi verdiene til r og av φ. Hvis vi ser på figuren, er verdien av r tilsvarer hypotenusen til en rett trekant. Bena er verdt til Y b, O vel x Y Y.
Fra binomial eller binomial form kan vi bevege oss til polarformen ved å:
r = √xto+Yto
Vinkelen φ Det er den som danner segmentet r med den horisontale aksen eller den imaginære aksen. Det er kjent som argument av det komplekse tallet. På denne måten:
φ = arctg (y / x)
Argumentet har uendelige verdier, og tar i betraktning at hver gang en sving som er verdt 2π radianer, inntar r den samme posisjonen igjen. På denne generelle måten uttrykkes argumentet til z, betegnet Arg (z) slik:
Arg (z) = φ + 2kπ
Der k er et helt tall og brukes til å indikere antall svinger som er slått: 2, 3, 4…. Skiltet indikerer rotasjonsretningen, hvis den er med eller mot klokken.
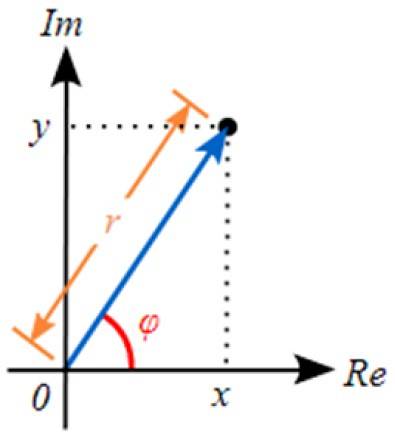
Og hvis vi vil gå fra polarform til binomialform, bruker vi de trigonometriske forholdene. Fra forrige figur kan vi se at:
x = r cos φ
y = r sin φ
På denne måten z = r (cos φ + i sin φ)
Som forkortes slik:
z = r cis φ
Eksempler på komplekse tall
Følgende komplekse tall er gitt i binomial form:
a) 3 + i
b) 4
d) -6i
Og disse i form av et bestilt par:
a) (-5, -3)
b) (0, 9)
c) (7.0)
Til slutt er denne gruppen gitt i polær eller trigonometrisk form:
a) √2 cis 45º
b) √3 cis 30º
c) 2 cis 315º
Hva er de for?
Nytten av komplekse tall går utover å løse den kvadratiske ligningen som ble vist i begynnelsen, siden de er essensielle innen ingeniørfag og fysikk, spesielt i:
-Studiet av elektromagnetiske bølger
-Vekselstrøm og spenningsanalyse
-Modellering av alle slags signaler
-Relativitetsteori, der tid antas å være en innbilt størrelse.
Komplekse nummeroperasjoner
Med komplekse tall kan vi utføre alle operasjonene som gjøres med ekte. Noen er lettere å gjøre hvis tallene kommer i binomial form, for eksempel addisjon og subtraksjon. I stedet er multiplikasjon og deling enklere hvis de utføres med polarformen.
La oss se på noen eksempler:
- Eksempel 1
Legg til z1 = 2 + 5i og zto = -3 -8i
Løsning
De virkelige delene legges til separat fra de imaginære delene:
z1 + zto = (2 + 5i) + (-3 -8i) = -1 -3i
- Eksempel 2
Multipliser z1 = 4 cis 45º og zto = 5 cis 120º
Løsning
Det kan vises at produktet av to komplekse tall i polær eller trigonometrisk form er gitt av:
z1 . zto = r1.rto cis (φ1 + φto)
I følge dette:
z1 . zto = (4 × 5) cis (45 + 120) = 20 cis 165º
App
En enkel anvendelse av komplekse tall er å finne alle røttene til en polynomligning som den som ble vist i begynnelsen av artikkelen.
Når det gjelder ligningen xto - 10x + 34 = 0, når vi bruker løsningsformelen får vi:

Derfor er løsningene:
x1 = 5 + 3i
xto = 5 - 3i
Referanser
- Earl, R. Komplekse tall. Gjenopprettet fra: maths.ox.ac.uk.
- Figuera, J. 2000. Matematikk 1.. Diversifisert. CO-BO utgaver.
- Hoffmann, J. 2005. Utvalg av matematikkemner. Monfort-publikasjoner.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Wikipedia. Komplekse tall. Gjenopprettet fra: en.wikipedia.org



Ingen har kommentert denne artikkelen ennå.