Sammensatte tallegenskaper, eksempler, øvelser

De sammensatte tall er de heltallene som har mer enn to delere. Hvis vi ser nøye på, er alle tall i det minste delbare nøyaktig av seg selv og av 1. De som bare har disse to delene kalles primtall, og de som har flere er forbindelser..

La oss se på tallet 2, som bare kan deles mellom 1 og 2. Nummeret 3 har også to deler: 1 og 3. Derfor er de begge primære. La oss nå se på tallet 12, som vi kan dele nøyaktig med 2, 3, 4, 6 og 12. Ved å ha 5 delere er 12 et sammensatt tall.

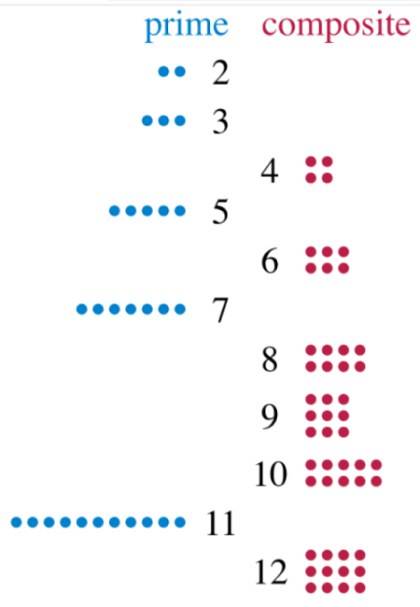
Og hva skjer med tallet 1, den som deler alle de andre? Vel, det er ikke prime, fordi det ikke har to delere, og det er ikke sammensatt, derfor faller 1 ikke inn i noen av disse to kategoriene. Men det er mange, mange flere tall som gjør det..

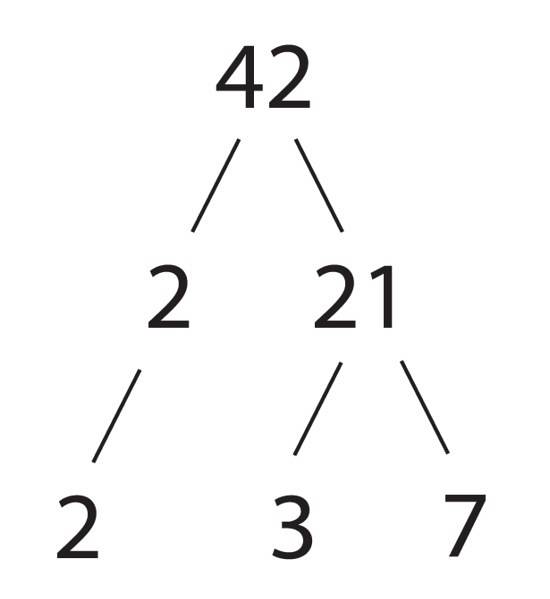
Sammensatte tall kan uttrykkes som produktet av primtall, og dette produktet, unntatt rekkefølgen av faktorene, er unikt for hvert tall. Dette er garantert av den grunnleggende regningen om regning bevist av den greske matematikeren Euklid (325-365 f.Kr.).

La oss gå tilbake til nummer 12, som vi kan uttrykke på forskjellige måter. La oss prøve noen:

12 = 4 x 3 = 2 x 6 = 12 x 1 = 2^to x 3 = 3 x 2^to = 3 x 2 x 2 = 2 x 2 x 3 = 2 x 3 x 2

Formene som er uthevet med fet skrift er produkter med primtall, og det eneste som endres er rekkefølgen på faktorene, som vi vet ikke endrer produktet. De andre skjemaene, selv om de er gyldige for å uttrykke 12, består ikke bare av primtall.

Eksempler på sammensatte tall

Hvis vi vil dekomponere et sammensatt tall i dets primfaktorer, må vi dele det mellom primtall på en slik måte at inndelingen er nøyaktig, det vil si at resten er 0.

Denne prosedyren kalles primtallsfaktorisering eller kanonisk nedbrytning. Primære faktorer kan løftes til positive eksponenter.

Vi skal nedbryte tallet 570, og merke oss at det er jevnt og derfor delbart med 2, som er et primtall.

Vi bruker en skråstrek for å skille tallet til venstre fra skillelinjene til høyre. De respektive kvotientene plasseres under nummeret etter hvert som de oppnås. Nedbrytningen er fullført når den siste figuren i venstre kolonne er 1:

570 │2
285 │

Når vi deler med 2, er kvotienten 285 som kan deles med 5, et annet primtall som ender på 5.

570 │2
285 5
57 │

57 er delelig med 3, også et primtall, siden summen av sifrene 5 + 7 = 12 er et multiplum av 3.

570 │2
285 5
57 3
19 │

Til slutt får vi 19, som er et primtall, hvis delere er 19 og 1:

570 │2
285 5
57 3
19-19
1 │

Ved å skaffe 1 kan vi allerede uttrykke 570 på denne måten:

570 = 2 x 5 x 3 x 19

Og vi ser at det i virkeligheten er et produkt av 4 primtall.

I dette eksemplet starter vi med å dele med 2, men de samme faktorene (i en annen rekkefølge) ville blitt oppnådd hvis vi for eksempel begynte med å dele med 5.

Delbarhetskriterier

For å spalte et sammensatt tall i hovedfaktorene, er det nødvendig å dele det nøyaktig. Kriteriene for delbarhet mellom primtall er regler som gjør det mulig å vite når et tall kan deles av en annen nøyaktig, uten å måtte prøve eller bevise.

-Delbarhet med 2

Alle partall, de som ender på 0 eller et partall, kan deles med 2.

-Delbarhet med 3

Hvis summen av sifrene til et tall er et multiplum av 3, er tallet også delbart med 3.

-Delbarhet med 5

Tall som slutter på 0 eller 5 kan deles med 5.

-Delbarhet med 7

Et tall kan deles med 7 hvis den siste sifferet skilles fra, multipliseres med 2 og trekker fra det gjenværende tallet, er den resulterende verdien et multiplum av 7.

Denne regelen virker litt mer komplisert enn de forrige, men i virkeligheten er den ikke så mye, så la oss se på et eksempel: vil 98 være delelig med 7?

La oss følge instruksjonene: vi skiller den siste figuren som er 8, vi multipliserer den med 2 som gir 16. Tallet som gjenstår når vi skiller 8 er 9. Vi trekker 16 - 9 = 7. Og siden 7 er et multiplum av seg selv , 98 kan deles mellom 7.

-Delbarhet med 11

Hvis summen av figurene i jevn stilling (2, 4, 6 ...) blir trukket fra summen av tallene i odde posisjon (1, 3, 5, 7 ...) og 0 eller et multiplum av 11 oppnås, blir tallet er delelig med 11.

De første multiplene på 11 kan lett identifiseres: de er 11, 22, 33, 44 ... 99. Men vær forsiktig, 111 er ikke, i stedet er 110.

Som et eksempel, la oss se om 143 er et multiplum av 11.

Dette tallet har 3 sifre, det eneste jevne sifferet er 4 (det andre), de to odde sifrene er 1 og 3 (første og tredje), og summen er 4.

Begge summene er trukket fra: 4 - 4 = 0 og siden 0 oppnås, viser det seg at 143 er et multiplum av 11.

-Delbarhet med 13

Tallet uten ensifferet må trekkes fra 9 ganger tallet. Hvis tellingen returnerer 0 eller et multiplum av 13, er tallet et multiplum av 13.

Som et eksempel vil vi verifisere at 156 er et multiplum av 13. Ensifret er 6 og tallet som forblir uten det er 15. Vi multipliserer 6 x 9 = 54 og nå trekker vi fra 54 - 15 = 39.

Men 39 er 3 x 13, så 56 er et multiplum av 13.

Primtall til hverandre

To eller flere primtall eller sammensatte tall kan være primtall eller samprime. Dette betyr at den eneste fellesdeleren de har er 1.

Det er to viktige egenskaper å huske når det kommer til coprimes:

-To, tre og flere påfølgende tall er alltid primære for hverandre.

-Det samme kan sies for to, tre eller flere oddetall på rad.

For eksempel er 15, 16 og 17 primtall for hverandre, og det samme er 15, 17 og 19.

Hvordan vite hvor mange delere et sammensatt tall har

Et primtall har to delere, det samme tallet og 1. Og hvor mange delere har et sammensatt tall? Disse kan være fettere eller forbindelser.

La N være et sammensatt tall uttrykt i form av dets kanoniske nedbrytning som følger:

N = aⁿ . b^m. c^s... r^k

Der a, b, c ... r er de viktigste faktorene og n, m, p ... k de respektive eksponentene. Antall delere C som N har er gitt av:

C = (n +1) (m + 1) (p +1) ... (k + 1)

Med C = primærdelere + sammensatte delere + 1

For eksempel 570, som uttrykkes slik:

570 = 2 x 5 x 3 x 19

Alle hovedfaktorene er hevet til 1, derfor har 570:

C = (1 + 1) (1 + 1) (1+ 1) (1 +1) = 16 delere

Av disse 10 delerne vet vi allerede: 1, 2, 3, 5, 19 og 570. Det mangler 10 flere divisorer, som er sammensatte tall: 6, 10, 15, 30, 38, 57, 95, 114, 190 og 285. De blir funnet ved å observere nedbrytningen i hovedfaktorer og også multiplisere kombinasjoner av disse faktorene sammen..

Løst øvelser

- Øvelse 1

Nedbryt følgende tall i hovedfaktorer:

a) 98

b) 143

c) 540

d) 3705

Løsning til

98 │2
49 │7
7 │7
1 │

98 = 2 x 7 x 7

Løsning b

143 11
13-13
1 │

143 = 11 x 13

Løsning c

540 │5
108 │2
54 │2
27 │3
9 │3
3 │3
1 │

540 = 5 x 2 x 2 x 3 x 3 x 3 = 5 x 2^to x 3³

Løsning d

3705 5
741 │3
247 13
19-19
1 │

3705 = 5 x 3 x 13 x 19

- Øvelse 2

Finn ut om følgende tall er primære for hverandre:

6, 14, 9

Løsning

-Delene på 6 er: 1, 2, 3, 6

-Når det gjelder de 14, er den delelig med: 1, 2, 7, 14

-Endelig har 9 deler: 1, 3, 9

Den eneste deleren de har til felles er 1, derfor er de primære for hverandre.

Referanser

1. Baldor, A. 1986. Aritmetikk. Codex-utgaver og distribusjoner.
2. Byju's. Prim og komposittall. Gjenopprettet fra: byjus.com.
3. Primtall og sammensatte tall. Gjenopprettet fra: profeyennyvivaslapresentacion.files.wordpress.com
4. Smartick. Delbarhetskriterier. Gjenopprettet fra: smartick.es.
5. Wikipedia. Sammensatte tall. Gjenopprettet fra: en.wikipedia.org.