De irrasjonelle tall er de hvis desimaluttrykk har uendelige tall uten et gjentatt mønster, derfor kan de ikke oppnås ved å lage kvotienten mellom to heltall.
Blant de mest kjente irrasjonelle tallene er:
Blant dem er uten tvil π (pi) den mest kjente, men det er mange flere. Alle tilhører settet med reelle tall, som er det numeriske settet som grupperer rasjonelle og irrasjonelle tall..
Ellipsen i figur 1 indikerer at desimalene fortsetter på ubestemt tid. Det som skjer er at plassen til vanlige kalkulatorer bare tillater å vise noen få.
Hvis vi ser nøye, når vi lager kvotienten mellom to hele tall, får vi en desimal med begrensede tall eller hvis ikke, med uendelige figurer der en eller flere blir gjentatt. Vel, dette skjer ikke med irrasjonelle tall..
Artikkelindeks
Den store eldgamle matematikeren Pythagoras, født 582 f.Kr. i Samos, Hellas, grunnla den pytagoreiske tankeskolen og oppdaget den berømte setningen som bærer navnet hans. Vi har det her til venstre (kanskje babylonerne allerede visste det lenge før).
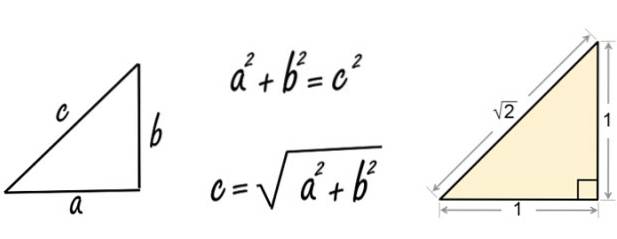
Da Pythagoras (eller sannsynligvis en disippel av ham) brukte setningen på en høyre trekant med sider lik 1, fant han det irrasjonelle tallet √2.
Han gjorde det på denne måten:
c = √1to + 1to = √1 + 1 = √2
Og umiddelbart skjønte han at dette nye tallet ikke kom fra kvotienten mellom to andre naturlige tall, som var de som var kjent på den tiden.
Derfor kalte han det irrasjonell, og oppdagelsen forårsaket stor angst og forvirring blant pythagoreerne.
-Settet med alle irrasjonelle tall er betegnet med bokstaven I og noen ganger som Q * eller QC. Forbindelsen mellom de irrasjonelle tallene I eller Q * og de rasjonelle tallene Q, gir opphav til settet med reelle tall R.
-Med irrasjonelle tall kan de kjente aritmetiske operasjonene utføres: addisjon, subtraksjon, multiplikasjon, divisjon, empowerment og mer.
-Divisjon med 0 er heller ikke definert mellom irrasjonelle tall.
-Summen og produktet mellom irrasjonelle tall er ikke nødvendigvis et annet irrasjonelt tall. For eksempel:
√2 x √8 = √16 = 4
Og 4 er ikke et irrasjonelt tall.
-Summen av et rasjonelt tall pluss et irrasjonelt tall resulterer imidlertid i et irrasjonelt. På denne måten:
1 + √2 = 2.41421356237 ...
-Produktet av et annet rasjonelt tall enn 0 med et irrasjonelt tall er også irrasjonelt. La oss se på dette eksemplet:
2 x √2 = 2.828427125 ...
-Det omvendte av et irrasjonelt resulterer i et annet irrasjonelt tall. La oss prøve noen:
1 / √2 = 0,707106781 ...
1 / √3 = 0.577350269 ...
Disse tallene er interessante fordi de også er verdiene til noen trigonometriske forhold av kjente vinkler. De fleste av de trigonometriske forholdene er irrasjonelle tall, men det er unntak, for eksempel sin 30º = 0,5 = ½, som er rasjonell.
-I tillegg oppfylles kommutative og assosierende egenskaper. Hvis a og b er to irrasjonelle tall, betyr dette at:
a + b = b + a.
Og hvis c er et annet irrasjonelt tall, så:
(a + b) + c = a + (b + c).
-Den fordelende egenskapen til multiplikasjon med hensyn til tillegg er en annen kjent egenskap som også holder for irrasjonelle tall. I dette tilfellet:
a. (b + c) = a.b + a.c.
-En irrasjonell a har sitt motsatte: -a. Når de legges sammen er resultatet 0:
a + (- a) = 0
-Mellom to forskjellige begrunnelser er det minst ett irrasjonelt tall.
Den virkelige linjen er en horisontal linje der de reelle tallene ligger, hvor irrasjonelle er en viktig del.
For å finne et irrasjonelt tall på den virkelige linjen, i geometrisk form, kan vi bruke Pythagoras teorem, en linjal og et kompass.
Som et eksempel skal vi finne √5 på den virkelige linjen, som vi tegner en rett trekant med sider for x = 2 Y y = 1, som bildet viser:
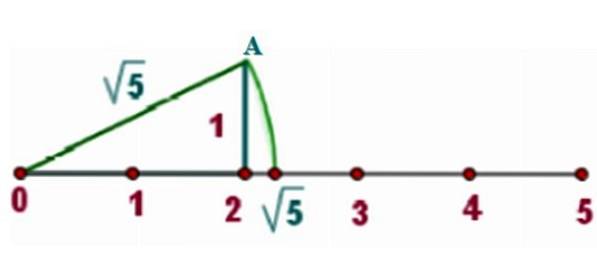
Av Pythagoras teorem er hypotenusen til en slik trekant:
c = √2to + 1to = √4 + 1 = √5
Nå er kompasset plassert med punktet 0, hvor en av toppunktene i høyre trekant også er. Poenget med kompassblyanten skal være i toppunkt A.
En bue av omkrets tegnes som skjærer til den virkelige linjen. Siden avstanden mellom sentrum av omkretsen og et hvilket som helst punkt på den er radiusen, som er lik √5, er skjæringspunktet også langt √5 fra sentrum.
Fra grafen kan det sees at √5 er mellom 2 og 2,5. En kalkulator gir oss den omtrentlige verdien av:
√5 = 2.236068
Og så, ved å bygge en trekant med passende sider, kan andre irrasjonelle være lokalisert, som √7 og andre.
Irrasjonelle tall er klassifisert i to grupper:
-Algebraisk
-Transcendent eller transcendental
Algebraiske tall, som kan eller ikke kan være irrasjonelle, er løsninger av polynomiske ligninger hvis generelle form er:
tiln xn + tiln-1xn-1 + tiln-2xn-2 +…. + a1x + aeller = 0
Et eksempel på en polynomligning er en kvadratisk ligning som denne:
x3 - 2x = 0
Det er lett å vise at det irrasjonelle tallet √2 er en av løsningene i denne ligningen.
På den annen side oppstår de transcendente tallene, selv om de er irrasjonelle, aldri som en løsning av en polynomligning.
De transcendente tallene som finnes hyppigst i anvendt matematikk er π, på grunn av dets forhold til omkretsen og tallet e, eller Eulers nummer, som er basen for naturlige logaritmer..
En grå firkant er plassert på en svart firkant i posisjonen som er angitt i figuren. Overflaten på den svarte firkanten er kjent for å være 64 cmto. Hvor mye er lengdene på begge rutene?
Arealet av et firkant med side L er:
A = L.to
Siden den svarte firkanten er 64 cmto av området, bør siden være 8 cm.
Denne målingen er den samme som diagonalen av den grå firkanten. Ved å bruke Pythagoras teorem på denne diagonalen, og huske at sidene av et kvadrat måler det samme, vil vi ha:
8to = Lgto + Lgto
Hvor Lg er siden av den grå firkanten.
Derfor: 2Lgto = 8to
Påføring av kvadratrot på begge sider av likheten:
Lg = (8 / √2) cm
Ingen har kommentert denne artikkelen ennå.