De transcendente tall er de som ikke kan oppnås som et resultat av en polynomligning. Det motsatte av et transcendent tall er a algebraisk nummer, som er løsninger av en polynomligning av typen:
tiln xn + tiln-1 xn-1 +… + Ato xto + til1 x + a0 = 0
Hvor koeffisientene an, tiln-1,… tilto, til1, til0 er rasjonelle tall, kalt polynomets koeffisienter. Hvis et tall x er en løsning på den forrige ligningen, er tallet ikke transcendent.
Vi vil analysere noen få tall og se om de er transcendente eller ikke:
a) 3 er ikke transcendent fordi det er en løsning av x - 3 = 0.
b) -2 kan ikke være transcendent fordi det er en løsning av x + 2 = 0.
c) ⅓ er en løsning av 3x - 1 = 0
d) En løsning av ligningen xto - 2x + 1 = 0 er √2 -1, slik at tallet per definisjon ikke er transcendent.
e) Det er heller ikke √2 fordi det er resultatet av ligningen xto - 2 = 0. Kvadrering √2 gir resultatet 2, som trekkes fra 2 er lik null. Så √2 er et irrasjonelt tall, men det er ikke transcendent.
Artikkelindeks
Problemet er at det ikke er noen generell regel for å få tak i dem (senere vil vi si en måte), men noen av de mest berømte er antallet pi og Neper nummer, betegnet henholdsvis med: π Y og.
Antallet π Det ser naturlig ut ved å observere at den matematiske kvotienten mellom omkretsen P av en sirkel og dens diameter D, uansett om den er en liten eller stor sirkel, alltid gir det samme tallet, kalt pi:
π = P / D ≈ 3.14159 ...
Dette betyr at hvis diameteren på omkretsen blir tatt som måleenhet, for alle, store eller små, vil omkretsen alltid være P = 3,14 ... = π, som kan sees i animasjonen i figur 2.
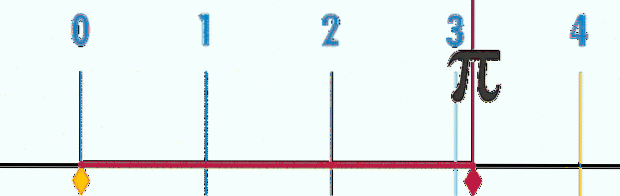
For å bestemme flere desimaler er det nødvendig å måle P og D med større presisjon og deretter beregne kvotienten, som er gjort matematisk. Poenget er at desimalene i kvotienten ikke har noen ende og aldri gjentar seg selv, så tallet π i tillegg til å være transcendent er det også irrasjonell.
Et irrasjonelt tall er et tall som ikke kan uttrykkes som delingen av to hele tall.
Det er kjent at hvert transcendente tall er irrasjonelt, men det er ikke sant at alle irrasjonelle tall er transcendente. For eksempel er √2 irrasjonell, men det er ikke transcendent.
Det transcendente tallet e er basen til naturlige logaritmer og dens desimale tilnærming er:
e ≈ 2.718281828459045235360 ... .
Hvis du ville skrive nummeret og nøyaktig, ville det være nødvendig å skrive uendelige desimaler, fordi hvert transcendente tall er irrasjonelt, som sagt før.
De ti første sifrene i og er enkle å huske:
2,7 1828 1828, og selv om det ser ut til å følge et repeterende mønster, oppnås dette ikke i desimalordre større enn ni.
En mer formell definisjon av og er den neste:
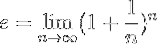
Noe som betyr at den eksakte verdien av og oppnås ved å utføre operasjonen som er angitt i denne formelen, når det naturlige tallet n har en tendens til uendelig.
Dette forklarer hvorfor vi bare kan få tilnærminger av og, siden uansett hvor stort tallet n er plassert, vil det alltid være mulig å finne et n høyere.
La oss se etter noen tilnærminger alene:
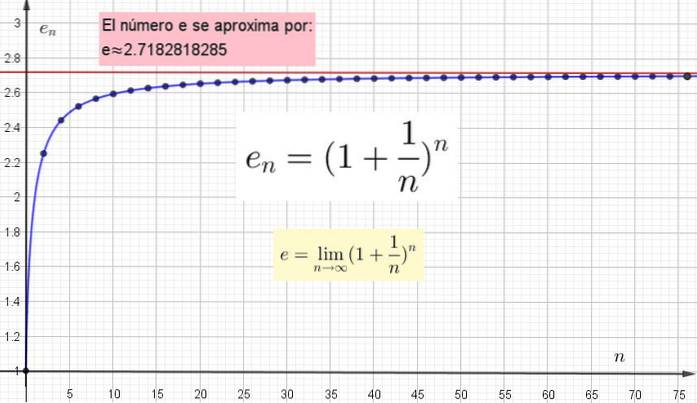
-Når n = 100 da (1 + 1/100)100 = 2,70481 som knapt sammenfaller i første desimal med den "sanne" verdien av e.
-Hvis du velger n = 10.000 har du (1 + 1 / 10.000)10.000 = 2.71815 som samsvarer med den "eksakte" verdien av e i de tre første desimalene.
Denne prosessen må følges uendelig for å oppnå den "sanne" verdien av e. Jeg tror ikke vi har tid til å gjøre det, men la oss prøve en til:
La oss bruke n = 100.000:
(1 + 1 / 100.000)100.000 = 2.7182682372
Det har bare fire desimaler som samsvarer med verdien som anses nøyaktig.
Det viktige er å forstå at jo høyere verdien av n valgt å beregne en, jo nærmere den er den sanne verdien. Men den sanne verdien vil bare være når n er uendelig.
Andre viktige tall
Bortsett fra disse berømte tallene, er det andre transcendente tall, for eksempel:
- to√2
Hvert algebraisk tall, annet enn 0 eller 1, hevet til en irrasjonell eksponent vil være et transcendent tall.
-Champernowne-nummeret i base 10:
C_10 = 0.123456789101112131415161718192021 ... .
-Champernowne-nummeret i base 2:
C_2 = 0.1101110010110111 ... .
-Gamma-tallet γ eller Euler-Mascheroni-konstanten:
γ ≈ 0,577 215 664 901 532 860 606
Som oppnås ved å gjøre følgende beregning:
γ ≈ 1 + ½ + ⅓ + ¼ +… + 1 / n - ln (n)
Når n være veldig veldig stor. For å ha den nøyaktige verdien av gammatallet, må du gjøre beregningen med n uendelig. Noe som ligner på det vi gjorde ovenfor.
Og det er mange flere transcendente tall. Den store matematikeren Georg Cantor, født i Russland og som bodde mellom 1845 og 1918, viste at settet med transcendente tall er mye større enn settet med algebraiske tall.
P = π D = 2 π R, hvor P er omkretsen, D diameteren og R omkretsens radius. Det skal huskes at:
-Diameteren på omkretsen er det lengste segmentet som forbinder to punkter av det samme og som alltid passerer gjennom sentrum,
-Radien er halvparten av diameteren og er segmentet som går fra sentrum til kanten.
A = π Rto = ¼ π Dto
S = 4 π Rto.
Ja, selv om det kanskje ikke virker som det, er overflaten til en sfære den samme som for fire sirkler med samme radius som sfære..
V = 4/3 π R3
Pizzeriaen “EXÓTICA” selger pizza med tre diametre: små 30 cm, middels 37 cm og store 45 cm. Et barn er veldig sulten, og han skjønte at to små pizzaer koster det samme som en stor. Hva vil være bedre for ham, kjøp to små pizzaer eller en stor?
Jo større område, jo større mengde pizza, av denne grunn blir arealet av en stor pizza beregnet og sammenlignet med to små pizzaer:
Stort pizzaområde = ¼ π Dto = ¼ ⋅3.1416⋅45to = 1590,44 cmto
Lite pizzaområde = ¼ π dto = ¼ ⋅3.1416⋅30to = 706,86 cmto
Derfor vil to små pizzaer ha et område på
2 x 706,86 = 1413,72 cmto .
Det er klart: du vil ha mer pizza når du kjøper en stor en enn to små.
“EXÓTICA” pizzeria selger også en halvkuleformet pizza med en radius på 30 cm til samme pris som en rektangulær form med en side på 30 x 40 cm. Hvilket ville du valgt?
Som nevnt i forrige avsnitt, er overflatearealet til en kule fire ganger så stor som en sirkel med samme diameter, så en halvkule på 30 cm i diameter vil ha:
12 '' halvkuleformet pizza: 1413,72 cmto (to ganger et sirkulært med samme diameter)
Rektangulær pizza: (30 cm) x (40 cm) = 1200 cmto .
Den halvkuleformede pizzaen har et større område.
Ingen har kommentert denne artikkelen ennå.