
Omkrets av sirkelen hvordan du får den ut og formler, løste øvelser

De sirkel omkrets er settet med punkter som danner omrisset av en sirkel og er også kjent som lengde av omkretsen. Det avhenger av radiusen, siden en større omkrets åpenbart vil ha en større kontur.
Være P omkretsen av en sirkel og R radiusen av den, så kan vi beregne P med følgende ligning:
P = 2π.R

Der π er et reelt tall (les “pi”) som er verdt omtrent 3,1416 ... Ellipsen skyldes at π har uendelige desimaler. Derfor, når du gjør beregninger, er det nødvendig å avrunde verdien.
For de fleste applikasjoner er det imidlertid nok å ta beløpet som er angitt her, eller å bruke alle desimalene som kalkulatoren du jobber med, returnerer..
Hvis det i stedet for å ha radius, er det foretrukket å bruke diameteren D, som vi vet er dobbelt så stor som radiusen, blir omkretsen uttrykt som følger:
P = π.2R = π.D
Siden omkretsen er en lengde, må den alltid uttrykkes i enheter som meter, centimeter, føtter, tommer og mer, avhengig av hvilket system som foretrekkes..
Artikkelindeks
- 1 Omkretser og sirkler
- 2 Demonstrasjonsøvelser for å beregne sirkelens omkrets
- 2.1 - Øvelse 1
- 2.2 - Øvelse 2
- 2.3 - Øvelse 3
- 3 applikasjoner
- 4 Referanser
Omkretser og sirkler
Dette er ofte begreper som brukes om hverandre, det vil si synonymt. Men det hender at det er forskjeller mellom dem.
Ordet "omkrets" kommer fra gresk "peri" som betyr kontur og "meter" eller mål. Omkretsen er omrisset eller omkretsen av sirkelen. Formelt er det definert som følger:
En sirkel er settet med punkter med lik avstand til et punkt som kalles sentrum, og denne avstanden er omkretsens radius.
For sin del er sirkelen definert som følger:
En sirkel er settet med punkter hvis avstand til et punkt kalt sentrum er mindre enn eller lik på en fast avstand kalt radio.
Leseren kan se den subtile forskjellen mellom de to begrepene. Omkretsen refererer bare til settet med kantene, mens sirkelen er settet med punkter fra kanten til det indre, hvorav omkretsen er grensen..
Øvelser ddemonstrasjon av beregning av sirkelens omkrets
Gjennom de følgende øvelsene vil konseptene som er beskrevet ovenfor bli praktisert, så vel som noen andre som vil bli forklart slik de ser ut. Vi starter fra det enkleste og vanskelighetsgraden vil gradvis øke.
- Øvelse 1
Finn omkretsen og arealet av sirkelen med en radius på 5 cm.
Løsning
Ligningen gitt i begynnelsen brukes direkte:
P = 2π.R= 2π,5 cm = 10 π cm = 31,416 cm
For å beregne arealet TIL følgende formel brukes:
TIL = π.Rto = π. (5cm)to= 25π cmto= 78,534 cmto
- Øvelse 2
a) Finn omkretsen og området til det blanke området i følgende figur. Sentrum av den skyggelagte sirkelen er på det røde punktet, mens midten av den hvite sirkelen er det grønne punktet.
b) Gjenta forrige avsnitt for det skyggelagte området.
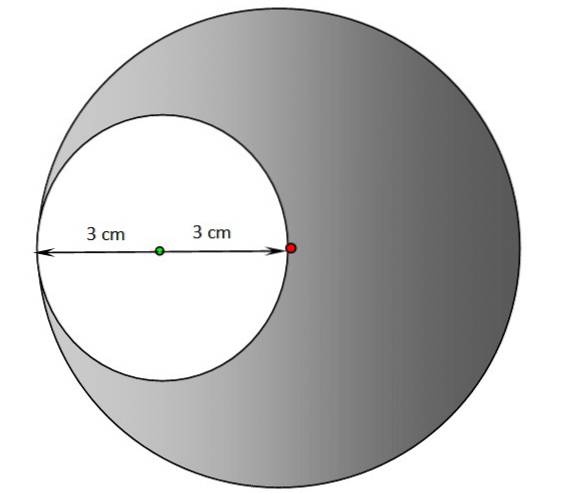
Løsning
a) Radien til den hvite sirkelen er 3 cm, derfor bruker vi de samme ligningene som i øvelse 1:
P = 2π.R= 2π,3 cm = 6 π cm = 18,85 cm
TIL = π.Rto = π. (3cm)to= 9π cmto= 28,27 cmto
b) For den skyggelagte sirkelen er radiusen 6 cm, omkretsen er dobbelt så stor som beregnet i del a):
P = 2π.R= 2π,6 cm = 12 π cm = 37,70 cm
Og til slutt beregnes området i det skyggelagte området slik:
- Først finner vi området av den skyggelagte sirkelen som om den var komplett, som vi vil kalle A ', slik:
TIL' = π.Rto= π. (6 cm)to = 36π cmto= 113,10 cmto
- Så til området TIL' Området til den hvite sirkelen trekkes fra, tidligere beregnet i avsnitt a), på denne måten oppnås det etterspurte området, som bare betegnes som A:
A = A '- 28,27 cmto = 113,10-28,27 cmto = 84,83 cmto
- Øvelse 3
Finn området og omkretsen til det skyggelagte området i følgende figur:
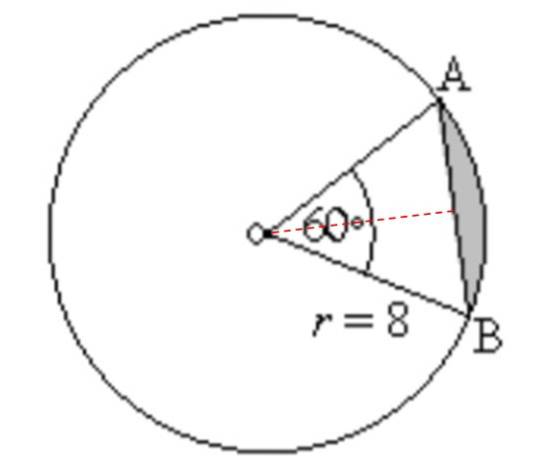
Løsning
Beregning av arealet til det skyggelagte området
Vi beregner først arealet av sirkulær sektor eller kil mellom de rette segmentene OA og OB og det sirkulære segmentet AB, som vist i følgende figur:
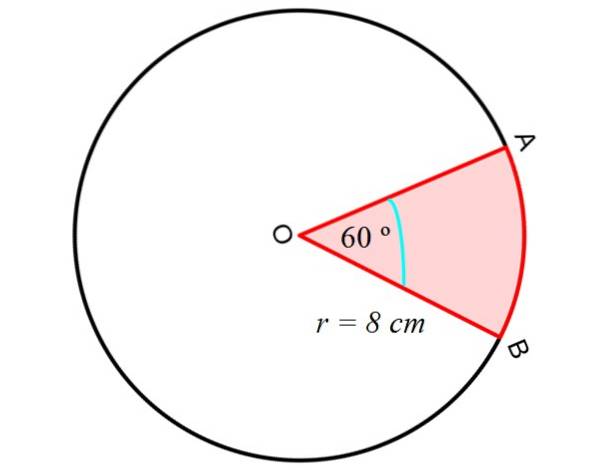
For dette brukes følgende ligning, som gir oss arealet til en sirkulær sektor, og vet radiusen R og den sentrale vinkelen mellom segmentene OA og OB, det vil si to av radiene til omkretsen:
TIL sirkulær sektor = Π.Rto. (αº / 360º)
Der αº er den sentrale vinkelen - er den sentral fordi toppunktet er sentrum for omkretsen - mellom to radier.
Trinn 1: beregne arealet til sirkulær sektor
Dermed er sektorområdet vist i figuren:
TIL sirkulær sektor = Π.Rto. (αº / 360º) = π. (8 cm)to. (60º / 360º) = (64/6) π cmto= 33,51 cmto
Trinn 2: beregne arealet til trekanten
Deretter beregner vi arealet til den hvite trekanten i figur 3. Denne trekanten er liksidig og dens areal er:
TIL triangel = (1/2) base x høyde
Høyden er den røde stiplede linjen sett i figur 4. For å finne den kan du for eksempel bruke Pythagoras teorem. Men det er ikke den eneste måten.
Den observante leseren vil ha lagt merke til at den likesidige trekanten er delt inn i to identiske høyre trekanter, hvis base er 4 cm:
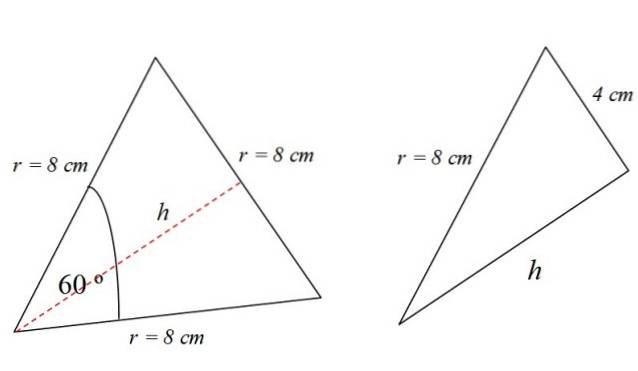
I en rett trekant oppfylles den pythagoreiske satsen, derfor:

TIL triangel = (1/2) bunn x høyde = (1/2) 8 cm x 6,93 cm = 27,71 cmto.
Trinn 3: Beregning av det skyggelagte området
Det er nok å trekke det større området (det av sirkulær sektor) fra det mindre området (det av den likesidige trekanten): A skyggelagt område = 33,51 cmto - 27,71 cmto = 5,80 cmto.
Beregning av omkretsen til det skyggelagte området
Den søkte omkretsen er summen av den rettlinte siden på 8 cm og buen med omkrets AB. Nå, den komplette omkretsen undergraver 360 º, derfor er en bue som danner 60 º en sjettedel av den totale lengden, som vi vet er 2.π.R:
AB = 2.π.R / 6 = 2.π.8 cm / 6 = 8.38 cm
Erstatter omkretsen av det skyggelagte området er:
P = 8 cm + 8,38 cm = 16,38 cm.
applikasjoner
Omkretsen, som området, er et veldig viktig begrep innen geometri og med mange bruksområder i det daglige..
Kunstnere, designere, arkitekter, ingeniører og mange andre mennesker bruker omkretsen mens de utvikler sitt arbeid, spesielt det som en sirkel, siden den runde formen er overalt: fra reklame, gjennom mat til maskiner.

For å kjenne lengden på en omkrets direkte, er det nok å pakke den inn med en tråd eller streng, og deretter utvide denne tråden og måle den med et målebånd. Det andre alternativet er å måle radius eller diameter på sirkelen og bruke en av formlene beskrevet ovenfor..
I det daglige arbeidet brukes begrepet perimeter når:
-Riktig form er valgt for en bestemt størrelse på pizza eller kake.
-En byvei skal utformes ved å beregne størrelsen på et hetteglass der biler kan snu for å endre retning.
-Vi vet at jorden kretser rundt solen i en omtrent sirkulær bane - planetbaner er faktisk elliptiske, i følge Keplers lover - men omkretsen er en veldig god tilnærming for de fleste planeter..
-Den passende størrelsen på en ring er valgt for å bli kjøpt i en nettbutikk.
-Vi velger en skiftenøkkel av riktig størrelse for å løsne en mutter.
Og mange flere.
Referanser
- Gratis matematikkopplæringer. Areal og omkrets av en sirkel - Geometri Kalkulator. Gjenopprettet fra: analyzemath.com.
- Math Open Reference. Omkrets, omkrets av en sirkel. Gjenopprettet fra: mathopenref.com.
- Monterey Institute. Omkrets og område. Gjenopprettet fra: montereyinstitute.org.
- Vitenskapelig. Hvordan finne omkretsen av en sirkel. Gjenopprettet fra: sciencing.com.
- Wikipedia. Omkrets. Gjenopprettet fra: en.wikipedia.org.



Ingen har kommentert denne artikkelen ennå.