De elektrisk potensial den defineres når som helst der et elektrisk felt eksisterer, som den potensielle energien til det feltet per enhetsladning. Punktladninger og punkt- eller kontinuerlige ladningsfordelinger produserer et elektrisk felt og har derfor et tilhørende potensial.
I det internasjonale systemet for enheter (SI) måles det elektriske potensialet i volt (V) og betegnes som V. Matematisk uttrykkes det som:
V = U / qeller
Hvor U er den potensielle energien forbundet med ladningen eller fordelingen og qeller det er en positiv testladning. Siden U er en skalar, er potensialet det også.
Fra definisjonen er 1 volt rett og slett 1 Joule / Coulomb (J / C), der Joule er SI-enheten for energi og Coulomb (C) er enheten for elektrisk ladning..
Anta en poengladning q. Vi kan sjekke arten av feltet som denne ladningen produserer ved å bruke en liten, positiv testladning, kalt qeller, brukt som sonde.
Arbeidet W trengte for å flytte denne lille lasten fra punktet til til poenget b, er det negative av forskjellen på potensiell energi ΔU mellom disse punktene:
Wa → b = -ΔU = - (Ub - ELLERtil)
Deler alt mellom qeller:
Wa → b / qeller= - ΔU / qeller = - (Ub - ELLERtil) / qeller = - (V.b - Vtil) = -AV
Her Vb er potensialet ved punkt b og Vtil er det i punkt a. Den potensielle forskjellen Vtil - Vb er potensialet i om b og kalles Vab. Rekkefølgen til abonnementene er viktig. Hvis den ble endret, ville den representere potensialet i b med hensyn til a.
Artikkelindeks
Av det foregående følger det at:
-AV = Wa → b / qeller
Derfor:
AV = -Wa → b / qeller
Nå beregnes arbeidet som integral av skalarproduktet mellom den elektriske kraften F mellom q og qeller og forskyvningsvektoren dℓ mellom punkt a og b. Siden det elektriske feltet er kraft per enhetsladning:
OG = F/ qeller
Arbeidet med å bære testbelastningen fra a til b er:
Denne ligningen gir deg muligheten til direkte å beregne potensialforskjellen hvis det elektriske feltet til ladningen eller fordelingen som produserer den tidligere er kjent..
Og det bemerkes også at potensialforskjellen er en skalar størrelse, i motsetning til det elektriske feltet, som er en vektor.
Fra den forrige definisjonen observerer vi at hvis OG og dℓ er vinkelrett, er potensialforskjellen AV null. Dette betyr ikke at potensialet på slike punkter er null, men at det bare er Vtil = Vb, det vil si at potensialet er konstant.
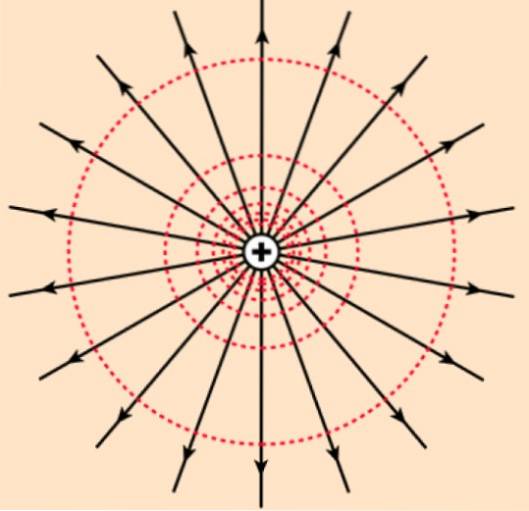
Linjene og overflatene der dette skjer kalles potensial. For eksempel er de ekvipotensielle linjene i feltet til en punktladning omkretser konsentriske til ladningen. Og de ekvipotensielle overflatene er konsentriske kuler.
Hvis potensialet produseres av en positiv ladning, hvis elektriske felt består av radiale linjer som projiserer ladningen, når vi beveger oss bort fra feltet, blir potensialet mindre og mindre. Som testbelastning qeller er positiv, føler du mindre elektrostatisk frastøting jo lenger du er fra q.
Tvert imot, hvis lasten hva er negativ, testladningen qeller (positivt) vil ha et lavere potensial når det kommer nærmere hva.
Integralet gitt ovenfor tjener til å finne potensialforskjellen, og derfor potensialet på et gitt punkt b, hvis referansepotensialet er kjent på et annet tidspunkt til.
For eksempel er det tilfellet med en punktbelastning hva, hvis elektriske feltvektor på et punkt som ligger på avstand r av lasten er:
OG = kq / rto r
Hvor k er den elektrostatiske konstanten hvis verdi i internasjonale systemenheter er:
k = 9 x 10 9 Nmto / Cto.
Og vektoren r er enhetsvektoren langs linjen som forbinder hva med punkt P.
Det erstattes i definisjonen av AV:
Velge det punktet b være på avstand r av ladningen og at når a → ∞ potensialet er 0, så er Vtil = 0 og forrige ligning er som:
V = kq / r
Velg Vtil = 0 når a → ∞ gir mening, fordi det på et punkt veldig langt fra belastningen er vanskelig å oppfatte at det eksisterer.
Når det er mange punktladninger fordelt i en region, beregnes det elektriske potensialet de produserer på et hvilket som helst punkt P i rommet, og legger til de individuelle potensialene som hver produserer. A) Ja:
V = V1 + Vto + V3 +… VN = ∑ VJeg
Summasjonen strekker seg fra i = til N, og potensialet for hver ladning beregnes ved hjelp av ligningen gitt i forrige avsnitt.
Med utgangspunkt i potensialet til en punktladning, kan vi finne potensialet som produseres av et ladet objekt, med en målbar størrelse, når som helst P.
For å gjøre dette er kroppen delt inn i mange små uendelig små ladninger dq. Hver bidrar til det fulle potensialet med en dV uendelig liten.
Deretter blir alle disse bidragene lagt til gjennom en integral, og dermed oppnås det totale potensialet:
Det er elektrisk potensial i forskjellige enheter, takket være det er mulig å skaffe elektrisk energi, for eksempel batterier, bilbatterier og stikkontakter. Elektriske potensialer er også etablert i naturen under elektriske stormer.
I celler og batterier lagres elektrisk energi gjennom kjemiske reaksjoner inni dem. Disse oppstår når kretsen er lukket, slik at likestrøm strømmer og en lyspære tennes, eller bilens startmotor fungerer..
Det er forskjellige spenninger: 1,5 V, 3 V, 9 V og 12 V er de vanligste.
Enheter og apparater som kjører på kommersiell vekselstrøm, er koblet til et innfelt stikkontakt. Avhengig av plassering kan spenningen være 120 V eller 240 V.
Det er den som oppstår under stormer på grunn av bevegelsen av elektrisk ladning gjennom atmosfæren. Det kan være i størrelsesorden 108 V.
Takket være et gummibånd produseres friksjonsladning som akkumuleres på en ledende kule plassert på toppen av en isolasjonssylinder. Dette genererer en potensiell forskjell som kan være flere millioner volt.
I hjertet er det spesialiserte celler som polariserer og depolariserer, og forårsaker potensielle forskjeller. Disse kan måles som en funksjon av tiden ved hjelp av et elektrokardiogram..
Denne enkle testen utføres ved å plassere elektroder på personens bryst, i stand til å måle små signaler..
Ettersom de er veldig lave spenninger, må du forsterke dem på en enkel måte og deretter ta dem opp på et papirbånd eller se dem gjennom datamaskinen. Legen analyserer pulsen for avvik og oppdager dermed hjerteproblemer.
Hjernens elektriske aktivitet kan også registreres med en lignende prosedyre, kalt EEG..
Mye Spørsmål = - 50,0 nC ligger 0,30 m fra punktet TIL og 0,50 m fra punkt B, som vist i følgende figur. Svar på følgende spørsmål:
a) Hva er potensialet i A produsert av denne ladningen?
b) Og hva er potensialet i B?
c) Hvis en ladning q beveger seg fra A til B, hva er den potensielle forskjellen den beveger seg gjennom?
d) I følge det forrige svaret, øker eller reduseres potensialet??
e) Hvis q = - 1.0 nC, hva er endringen i den elektrostatiske potensielle energien når den beveger seg fra A til B?
f) Hvor mye arbeid gjør det elektriske feltet produsert av Q når testladningen beveger seg fra A til B?
Q er en punktladning, derfor blir det elektriske potensialet i A beregnet av:
VTIL = kQ / rTIL = 9 x 109 x (-50 x 10-9) / 0,3 V = -1500 V
På samme måten
VB = kQ / rB = 9 x 109 x (-50 x 10-9) / 0,5 V = -900 V
AV = Vb - Vtil = -900 - (-1500) V = + 600 V
Hvis ladningen q er positiv, øker potensialet, men hvis det er negativt, reduseres potensialet.
ΔV = ΔU / qeller → ΔU = qeller AV = -1,0 x 10-9 x 600 J = -6,0 x 10-7 J.
Det negative logget inn ΔU indikerer at den potensielle energien i B er mindre enn A.
Siden W = -ΔU realiserer feltet seg +6,0 x 10-7 J av arbeid.
Ingen har kommentert denne artikkelen ennå.