
Relativt trykkformel, hvordan det beregnes, eksempler, trening
De trykkslektning på er den som måles med hensyn til en viss verdi eller datum, som vanligvis er atmosfæretrykket ved havnivå (standard atmosfæretrykk). Dette er hensiktsmessig fordi mye av trykkmålingene utføres under gasslagene som utgjør atmosfæren, som utøver sitt eget trykk..
I stedet måles absolutt trykk i forhold til et totalvakuum der det ikke er noen interagerende molekyler. I en beholder der det er laget vakuum er det ingen partikler som virker fra innsiden på veggene eller på gjenstander inni den..

Trykket som måles kan være over eller under atmosfærisk trykk. I det første tilfellet snakker vi om måler trykk og i den andre av vakuumtrykk.
Normalt er trykket som måles daglig i dekk og blodtrykk relativt trykk, mens når atmosfæretrykk måles ved hjelp av et barometer, er det et absolutt trykk.
Artikkelindeks
- 1 Formel for relativt trykk
- 2 Hvordan beregnes relativt trykk?
- 3 Trykkvariasjon med dybde
- 4 Eksempler på relativt trykk
- 4.1 Trykk på bunnen av et svømmebasseng
- 4.2 Trykk i et dekk
- 5 Øvelse løst
- 5.1 Løsning
- 6 Referanser
Relativt trykk formel
Å være det relative trykket er forskjellen mellom det absolutte trykket Pabs og atmosfærisk trykk Pminibank, det er et differensialtrykk eller trykkdifferanse. Ved det relative trykket Prel Det er kjent på engelsk som måler trykk Pg og er gitt av forholdet:
Pabs = Pminibank + Pg
Prel = Pabs - Pminibank
For trykk brukes pascal som måleenhet for det internasjonale systemet for enheter, uavhengig av om det er et absolutt trykk eller et relativt trykk..
Pascal er lik kraften som utøves av 1 newton på et område på 1 mto, men andre enheter brukes ofte, for eksempel millimeter kvikksølv, vann, angelsaksiske enheter som f.eks psi og andre.
Hvordan beregner du det relative trykket?
Hvis absolutt trykk ved et punkt og standard atmosfærisk trykk er kjent, er det relative trykket subtraksjonen mellom de to.
Anta for eksempel at det absolutte trykket i et bestemt system er 305 kPa. Å vite at standard atmosfæretrykk er 101,3 kPa, er det relative trykket:
Pg = Pabs - Pminibank = 305 - 101,3 kPa = 203,7 kPa
KPa eller kilopascal er tusen ganger større enn en pascal. Det brukes oftere, siden trykkverdiene er i størrelsesorden tusenvis av pascal. Vekten til et eple er omtrent 1 newton og en pascal er lik denne kraften fordelt over et kvadrat med en side på 1 meter. Andre multipler brukes også som megapascal (1 MPa = 1 x 106 Pa) eller gigapascal (1 GPa = 1x 109 Pa).
Trykket i eksemplet er måler fordi det er over atmosfærisk trykk, men det er absolutt trykk under det. For eksempel, hvis en gass i en beholder har et absolutt trykk på 50 kPa, er dens relative trykk et vakuumtrykk som produserer sug:
Pg = Pabs - Pminibank = 50 - 101,3 kPa = -51,3 kPa
I disse eksemplene ble standard atmosfæretrykk brukt, som er trykket ved havnivå. Men hvis det kreves større nøyaktighet i beregningen, kan det lokale atmosfæretrykket brukes, som kan avvike fra 101,3 kPa, siden det avhenger av høyden og andre geografiske forhold..
I tekstene er trykket som er gitt vanligvis relativt, og hvis det kreves å arbeide med absolutt trykk, skiller man disse ved bruk av abonnement for å unngå forvirring..
Trykkvariasjon med dybde
På hvert punkt inne i en væske som vann er det trykk. Forutsatt at vannet er ukomprimerbart, forblir dens tetthet konstant og trykket varierer vertikalt.
Det kan kontrolleres ved å ta en liten porsjon væske i form av en tykk plate dy som er i ro midt i væskemassen.
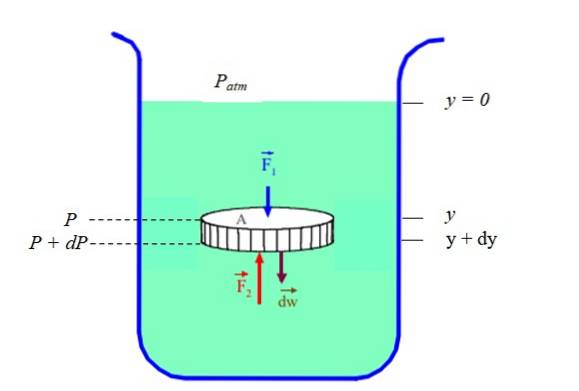
Kreftene på skivens sirkulære kanter avbrytes parvis, men ikke kreftene som utøves av massen av væske over og under skiven: F1 Y Fto. I tillegg er det nødvendig å vurdere vekten av væskeskiven dW i Newtons andre lov:
∑FY = Fto - F1 - W = 0
Disse kreftene kan uttrykkes i form av trykk, som er den vinkelrette kraften per arealenhet. På denne måten har vi trykket P, produsert av kraften F1:
F1 = P. A
Hvor A er sirkelområdet på disken. På samme måte:
Fto = (P + dP). TIL
Med P + dP trykket på dybden y + dy. Vekten er dW = dm. g:
(P + dP). A - P. A - dm. g = 0
Tettheten av væsken er ρ = dm / dV, med dV som volumet av væskeskiven, gitt av A.dy. På denne måten:
(P + dP). A - P. A - ρA.dy .g = 0
Ligningen som oppnås er forenklet til:
dP - ρgdy = 0 → dP = ρgdy
Integrering av begge sider fra og1 til ogto:
= Pto - P1 = ρg (ogto - Y1)
Begrepet Pto - P1 det er en trykkforskjell eller differensialtrykk. Hvis vi vil vite trykket ved det vertikale koordinatpunktet y, gjør vi det Y1 = 0, Yto = og Y Peller = Pminibank. Med dette vil vi ha trykket i forhold til dybden, som bare avhenger av dybden og:
Pto - Pminibank = ρgy ⇒ Prel = ρgy
Eksempler på relativt trykk
Trykk på bunnen av et svømmebasseng
Vi har alle opplevd presset fra å dykke ned i et basseng eller havet. Hva er det relative trykket som føltes når det senkes ned i et ferskvannsbasseng på en dybde på 5 meter? Ved å bruke forrige uttrykk, og vite at tettheten av ferskvann er 1000 kg / m3, med g = 9,81 m / sto det relative trykket er:
Prel = ρgy = 1000 x 9,81 x 5 Pa = 49050 Pa.
Trykk i et dekk
Bildekk har vanligvis et trykk på 32 psi. Dette er en måler eller relativt trykk i pund per kvadrattomme, enheten som brukes i engelsktalende land. Mange målere er kalibrert i disse enhetene. 32 psi tilsvarer 220632 Pa eller 220 kPa.
Treningen løst
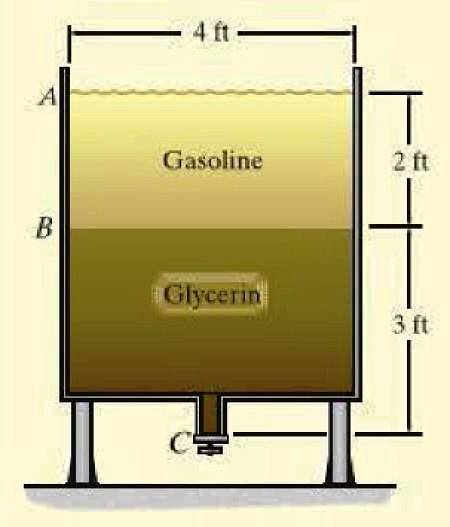
En tank inneholder bensin og glyserin, to blandbare væsker (de blandes ikke) i de angitte høydene. Hva er målertrykket i bunnen av tanken? De spesifikke vektene, betegnet med den greske bokstaven γ, for hver væske er festet:
γgass = 45,3 lb / ft3
γgly = 78,7 lb / ft3

Løsning
Den spesifikke tyngdekraften γ til en væske er produktet av dens tetthet og tyngdekraftakselerasjonen. Derfor kan ligningen av det relative trykket uttrykkes som følger:
Prel = γ.y
Det relative trykket i bunnen av tanken skyldes både vekten av glyserinkolonnen og bensinen og er uavhengig av tankens form:
Prel = γgass . YAB + γgly . YF.Kr. = (45,3 x 2 + 78,7 x 3) lb / ftto = 326,7 lb / ftto
Referanser
- Cimbala, C. 2006. Fluid Mechanics, Fundamentals and Applications. Mc. Graw bakke.
- Hibbeler, R. 2015. Fluid Mechanics. Første. Ed Pearson.
- Mott, R. 2006. Væskemekanikk. 4. plass Utgave. Pearson Education.
- Smits, A. 2006. Fluid Mechanics, A Physical Introduction. Alpha Omega.
- Streeter, V. 1999. Væskemekanikk. Mcgraw hill.
- Zapata, F. Trykk og dybde. Gjenopprettet fra: francesphysics.blogspot.com.


Ingen har kommentert denne artikkelen ennå.