
Sammensatt proporsjonalitetsforklaring, sammensatt regel på tre, øvelser
De sammensatt eller multiple proporsjonalitet Det er forholdet mellom mer enn to størrelser, hvor direkte og omvendt proporsjonalitet kan observeres mellom dataene og det ukjente. Dette er en mer avansert versjon av enkel proporsjonalitet, selv om teknikkene som brukes i begge prosedyrer er like..
For eksempel, hvis det trengs 7 personer for å losse 10 tonn varer på 3 timer, kan sammensatt proporsjonalitet brukes til å beregne hvor mange mennesker det vil ta å losse 15 tonn på 4 timer..
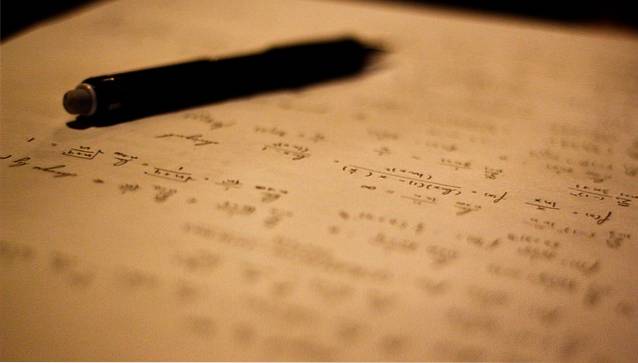
For å svare på dette spørsmålet er det praktisk å lage en verditabell for å studere og relatere størrelser og ukjente.
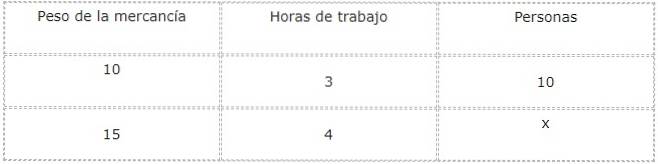
Vi fortsetter med å analysere typer forhold mellom hver størrelse og den nåværende ukjente, som i dette tilfellet tilsvarer antall personer som vil jobbe.
Når vekten på varene øker, øker også antall personer som skal lastes ned. På grunn av dette er forholdet mellom vekt og arbeidere direkte.
På den annen side, når antall arbeidstakere øker, reduseres arbeidstiden. På grunn av dette er forholdet mellom mennesker og arbeidstid av den omvendte typen.
Artikkelindeks
- 1 Hvordan beregne sammensatte proporsjoner
- 2 Forklaring
- 3 Direkte regel på tre
- 4 Omvendt regel på tre
- 5 Tilstand
- 6 Verifisering av resultater
- 7 Klarering
- 8 Historie
- 9 Løst øvelser
- 9.1 Øvelse 1
- 9.2 Øvelse 2
- 10 Foreslåtte øvelser
- 11 Referanser
Hvordan beregne sammensatte proporsjoner
For å løse eksempler som den ovenfor, brukes sammensatt regel av tre-metoden mest. Dette består i å etablere typer forhold mellom størrelser og ukjente og deretter representere et produkt mellom brøk.
Med hensyn til det første eksemplet er brøkene som tilsvarer verditabellen organisert som følger:
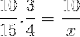
Men før du løser og løser det ukjente, må brøkene som tilsvarer det omvendte forholdet inverteres. Som for dette tilfellet tilsvarer den variable tiden. På denne måten vil operasjonen som skal løses være:
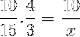
Hvis eneste forskjell er inversjonen av brøkdelen som tilsvarer tidsvariabelen 4/3. Vi fortsetter å operere og tømme verdien av x.
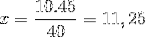
Dermed trengs mer enn elleve mennesker for å kunne laste ut 15 tonn med varer på 4 timer eller mindre.
Forklaring
Proporsjonalitet er det konstante forholdet mellom størrelser som kan endres, som vil være symmetrisk for hver av de involverte størrelsene. Det er direkte og omvendt proporsjonale forhold, og definerer dermed parametrene for enkel eller sammensatt proporsjonalitet.
Direkte regel på tre
Den består av et forhold mellom variabler, som viser den samme oppførselen når den modifiseres. Det er veldig hyppig i beregningen av prosentandeler som refererer til andre størrelser enn hundre, hvor dens grunnleggende struktur blir verdsatt.
Som et eksempel kan 15% av 63 beregnes. Ved første øyekast kan denne prosentandelen ikke lett forstås. Men ved å implementere regelen om tre, kan følgende forhold opprettes: hvis 100% er 63, så 15%, hvor mye vil det være?
100% - 63
15% -X
Og den tilsvarende operasjonen er:
(15%. 63) / 100% = 9,45
Hvor prosenttegnene er forenklet og tallet 9.45 er oppnådd, som representerer 15% av 63.
Omvendt regel på tre
Som navnet antyder, er forholdet mellom variablene i dette tilfellet det motsatte. Det omvendte forholdet må etableres før du går videre til beregningen. Prosedyren er homolog med den direkte regelen om tre, bortsett fra at investeringen i brøkdelen skal beregnes..
For eksempel trenger 3 malere 5 timer på å fullføre en vegg. Om hvor mange timer ville fire malere fullføre det?
I dette tilfellet er forholdet omvendt, ettersom antall malere øker, bør arbeidstiden reduseres. Forholdet er etablert;
3 malere - 5 timer
4 malere - X timer
Når forholdet er omvendt, blir rekkefølgen for operasjonen reversert. Dette er den riktige måten;
(3 malere). (5 timer) / 4 malere = 3,75 timer
Begrepet malere er forenklet, og resultatet er 3,75 timer.
Tilstand
For å være i nærvær av en forbindelse eller multiple proporsjonalitet, er det nødvendig å finne begge typer forhold mellom størrelser og variabler.
- Direkte: Variabelen har samme oppførsel som det ukjente. Det vil si at når den ene øker eller reduseres, endres den andre likt.
- Omvendt: Variabelen presenterer en antonymadferd til den ukjente. Fraksjonen som definerer nevnte variabel i verditabellen, må inverteres for å representere det omvendte proporsjonale forholdet mellom variabel og ukjent..
Verifisering av resultater
Det er veldig vanlig å forveksle størrelsesorden når du arbeider med sammensatte proporsjoner, i motsetning til hva som skjer i de vanlige proporsjonsberegningene, hvis natur stort sett er direkte og løselig ved hjelp av en enkel regel på tre..
Av denne grunn er det viktig å undersøke den logiske rekkefølgen på resultatene, verifisere sammenhengene i figurene produsert av regelen om tre sammensatte.
I det første eksemplet vil det å gjøre en slik feil resultere i 20 som resultatet. Det vil si 20 personer som skal laste av 15 tonn med varer på 4 timer.
Ved første øyekast ser det ikke ut som et sprøtt resultat, men det er merkelig en økning på nesten 200% i personalet (fra 7 til 20 personer) når økningen i varer er 50%, og til og med med større tidsrom til å utføre arbeidet.
På denne måten representerer den logiske verifiseringen av resultatene et viktig skritt når man implementerer regelen om tre sammensatte..
Klarering
Selv om det er mer grunnleggende i forhold til matematisk opplæring, er klarering et viktig skritt i tilfeller av proporsjonalitet. En feil klarering er nok til å ugyldiggjøre ethvert resultat oppnådd i den enkle eller sammensatte regelen på tre..
Historie
Regelen om tre ble kjent i Vesten gjennom araberne, med publikasjoner av forskjellige forfattere. Blant dem Al-Jwarizmi og Al-Biruni.
Takket være sin flerkulturelle kunnskap hadde Al-Biruni tilgang til omfattende informasjon om denne praksisen på sine reiser til India, og var ansvarlig for den mest omfattende dokumentasjonen om regelen om tre.
Han argumenterer i sin forskning om at India var det første stedet hvor bruken av regelen om tre ble vanlig. Forfatteren forsikrer at den ble utført på en flytende måte i sine direkte, inverse og til og med sammensatte versjoner..
Den nøyaktige datoen da regelen om tre ble en del av den matematiske kunnskapen i India, er fortsatt ukjent. Imidlertid ble det eldste dokumentet som adresserte denne praksisen, Bakhshali-manuskriptet, oppdaget i 1881. Det er for tiden i Oxford.
Mange historikere av matematikk hevder at dette manuskriptet stammer fra begynnelsen av denne tiden..
Løst øvelser
Øvelse 1
Et flyselskap må frakte 1535 personer. Det er kjent at med tre fly vil det ta 12 dager å få den siste passasjeren til destinasjonen. 450 flere personer har ankommet flyselskapet, og to fly er beordret reparert for å hjelpe til med denne oppgaven. Hvor mange dager vil det ta flyselskapet å overføre den siste passasjeren til destinasjonen?
Forholdet mellom antall personer og arbeidsdager er direkte, fordi jo større antall mennesker, jo flere dager vil det ta å utføre dette arbeidet..
På den annen side er forholdet mellom fly og dager omvendt proporsjonalt. Når antall fly øker, reduseres dagene som trengs for å overføre alle passasjerer.
Verditabellen som refererer til denne saken er laget.

Som beskrevet i det første eksemplet, må teller og nevner inverteres i brøkdelen som tilsvarer den inverse variabelen i forhold til det ukjente. Operasjonen er som følger:
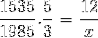
X = 71460/7675 = 9,31 dager
Det tar mer enn 9 dager å overføre personer fra 1985 med 5 fly.
Øvelse 2
En 25-tonns maisavling blir ført til lastebilene. Det er kjent at året før det tok dem 8 timer med en lønn på 150 arbeidere. Hvis lønnsveksten i år økte med 35%, hvor lang tid vil det ta å fylle lastebilene med en 40-tonns høst??
Før du representerer verditabellen, må antall arbeidere for dette året defineres. Dette økte med 35% fra det opprinnelige tallet på 150 arbeidere. For dette brukes en direkte regel på tre.
100% - 150
35% - X
X = (35,100) / 100 = 52,5. Dette er antall ekstra arbeidstakere i forhold til året før, og oppnådde et totalt antall arbeidere på 203, etter å ha avrundet det oppnådde beløpet.
Vi fortsetter med å definere den tilsvarende datatabellen

I dette tilfellet representerer vekten en variabel som er direkte relatert til den ukjente tiden. På den annen side har arbeidervariabelen et omvendt forhold til tiden. Jo større antall arbeidere, jo kortere arbeidsdag.
Når vi tar disse betraktningene i betraktning og inverterer brøkdelen som tilsvarer arbeidstakervariabelen, fortsetter vi å beregne.
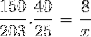
X = 40600/6000 = 6,76 timer
Dagen vil ta i underkant av 7 timer.
Foreslåtte øvelser
- Definer 73% av 2875.
- Beregn antall timer Teresa sover, hvis det er kjent at hun bare sover 7% av totalsummen for dagen. Definer hvor mange timer du sover i uken.
- En avis publiserer 2000 eksemplarer hver 5. time, og bruker bare to trykkmaskiner. Hvor mange eksemplarer vil han produsere på 1 time hvis han bruker 7 maskiner? Hvor lang tid tar det 10 000 eksemplarer ved bruk av 4 maskiner?
Referanser
- Leksikon Alvarez-innvielse. A. Álvarez, Antonio Álvarez Pérez. EDAF, 2001.
- Komplett grunnleggende og høyere primærinstruksjonshåndbok: for bruk av håpefulle lærere og spesielt studenter fra de normale skolene i provinsen, bind 1. Joaquín Avendaño. Utskrift av D. Dionisio Hidalgo, 1844.
- Rasjonell tilnærming av virkelige funksjoner. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3. mars. 2011.
- Elementær aritmetikk for undervisning i skoler og høyskoler i Mellom-Amerika. Darío González. Tips. Arenales, 1926.
- Studiet av matematikk: Om studiet og vanskeligheter med matematikk. Augustus De Morgan. Baldwin og Cradock, 1830.


Ingen har kommentert denne artikkelen ennå.