
Coplanar poengligning, eksempel og løste øvelser
De coplanar poeng de tilhører alle samme plan. To punkter er alltid i samme plan, siden disse punktene definerer en linje som uendelige fly passerer gjennom. Så tilhører begge punktene hvert av flyene som går gjennom linjen, og derfor vil de alltid være i samme plan.
På den annen side definerer tre punkter et enkelt plan, hvorfra det følger at tre punkter alltid vil være i samme plan som det planet de bestemmer..
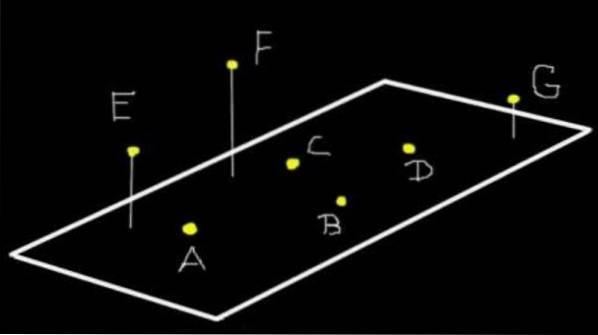
Mer enn tre poeng kan være i samme plan eller ikke. For eksempel, i figur 1, er punktene A, B, C og D i samme plan som (Ω) -planet. Men E, F og G er ikke plan til (Ω), selv om de er i samme plan som det de definerer.
Artikkelindeks
- 1 Ligning av et fly gitt tre poeng
- 2 Eksempel
- 2.1 Løsning
- 3 Løst øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 3.3 - Øvelse 3
- 3.4 - Øvelse 4
- 4 Referanser
Ligning av et fly gitt tre poeng
Ligningen til et plan bestemt av tre kjente punkter A, B, C er et matematisk forhold som garanterer at ethvert punkt P med generiske koordinater (x, y, z) som oppfyller ligningen tilhører nevnte plan.
Den forrige uttalelsen tilsvarer å si at hvis P av koordinatene (x, y, z) oppfyller ligningen til planet, vil punktet være i samme plan som de tre punktene A, B, C som bestemte planet.
For å finne ligningen til dette planet, la oss starte med å finne vektorene AB Y AC:
AB = [Bx - Axe, By - Ay, Bz - Az]
AC = [Cx - Ax, Cy - Ay, Cz - Az]
Vektorproduktet AB X AC resulterer i en vektor vinkelrett eller normal til planet bestemt av punktene A, B, C.
Ethvert punkt P av koordinatene (x, y, z) tilhører planet hvis vektoren AP er vinkelrett på vektoren AB X AC, som er garantert hvis:
AP • (AB X AC) = 0
Dette tilsvarer å si at det tredobbelte produktet av AP, AB Y AC er null. Ovennevnte ligning kan skrives i matriseform:
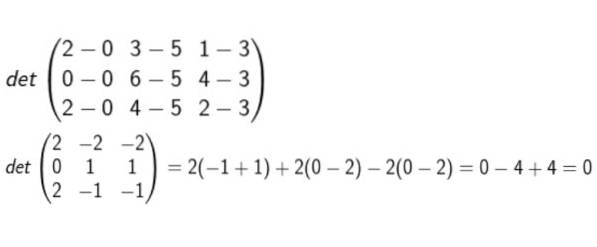
Eksempel
La punktene A (0, 1, 2); B (1, 2, 3); C (7, 2, 1) og D (til, 0, 1). Hvilken verdi skal den ha til slik at de fire punktene er i samme plan?
Løsning
For å finne verdien av a, må punkt D være en del av planet bestemt av A, B og C, som er garantert hvis det tilfredsstiller ligningen til planet.
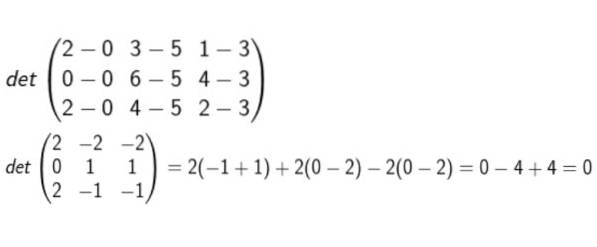
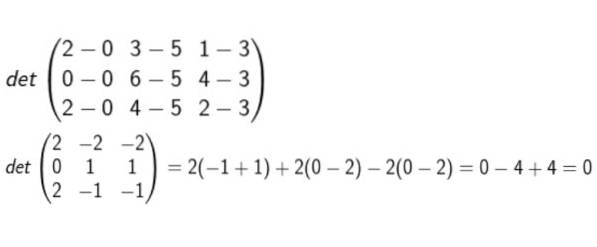
Utvikling av determinanten vi har:
a (-1-1) + 1 (-1 - 7) -1 (1-7) = -2a -8 + 6 = -2a - 2 = 0
Ovennevnte ligning forteller oss det a = -1 slik at likhet oppfylles. Med andre ord, den eneste måten som punkt D (til, 0,1) er i samme plan som punktene A, B og C er det til verdt -1. Ellers vil det ikke være i samme plan.
Løst øvelser
- Øvelse 1
Et plan krysser de kartesiske aksene X, Y, Z ved henholdsvis 1, 2 og 3. Krysset mellom dette planet og aksene bestemmer punktene A, B og C. Finn komponenten Dz til et punkt D, hvis kartesiske komponenter er:
D (-Dz, Dz + 1, Dz)
Forutsatt at D er i samme plan som punktene A, B og C.
Løsning
Når avskjæringen av et plan med de kartesiske aksene er kjent, kan segmentformen av ligningen av planet brukes:
x / 1 + y / 2 + z / 3 = 1
Siden punkt D må tilhøre forrige plan, må det:
-Dz / 1 + (Dz + 1) / 2 + Dz / 3 = 1
Nemlig:
-Dz + Dz / 2 + ½ + Dz / 3 = 1
Dz (-1 + ½ + ⅓) = ½
Dz (-1 / 6⅙) = ½
Dz = -3
Fra det ovenstående følger at punkt D (3, -2, -3) er i samme plan som punktene A (1, 0, 0); B (0, 2, 0) og C (0, 0, 3).
- Øvelse 2
Bestem om punktene A (0, 5, 3); B (0, 6, 4); C (2, 4, 2) og D (2, 3, 1) er av samme plan.
Løsning
Vi danner matrisen hvis rader er koordinatene til D-A, B-A og C-A. Deretter beregnes determinanten og det blir verifisert om den er null eller ikke.
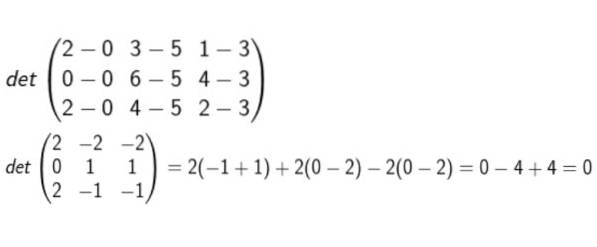
Etter å ha utført alle beregningene konkluderes det med at de er i samme plan.
- Øvelse 3
Det er to linjer i rommet. En av dem er linjen (R) hvis parametriske ligning er:
(R): x = 1 + 2 λ; y = 1 - λ; z = 1
Og den andre er linjen (S) hvis ligning er:
(S): x + 2 y = 1; z = -1
Vis at (R) og (S) er linjeplaner, det vil si at de ligger i samme plan.
Løsning
La oss starte med vilkårlig å ta to poeng på linjen (R) og to på linjen (S):
Rett (R): λ = 0; A (1, 1, 1) og λ = 1; B (3, 0, 1)
La oss gjøre x = 0 på linjen (S)=> y = ½; C (0, ½, -1). Og på den annen side, hvis vi gjør det y = 0 => x = 1; D (1, 0, -1).
Det vil si at vi har tatt punktene A og B som tilhører linjen (R) og punktene C og D som tilhører linjen (S). Hvis disse punktene er i samme plan, vil de to linjene også være i samme plan.
Nå velger vi punkt A som dreiepunkt, og så finner vi koordinatene til vektorene AB, AC Y AD. På denne måten får du:
B - A: (3-1, 0 -1, 1 - 1) => AB= (2, -1, 0)
C - A: (0-1, 1/2 -1, -1 - 1) => AC= (-1, -1/2, -2)
D - A: (1-1, 0 -1, -1 - 1) => AD= (0, -1, -2)
Det neste trinnet er å konstruere og beregne determinanten hvis første rad er koeffisientene til vektoren AB, den andre raden er de av AC og tredje rad de av vektoren AD:
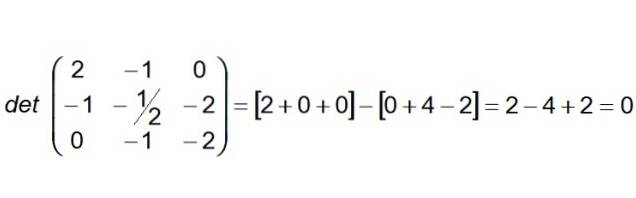
Siden determinanten viser seg å være null, kan vi konkludere med at de fire punktene er i samme plan. I tillegg kan det fastslås at linjene (R) og (S) også er i samme plan.
- Øvelse 4
Linjene (R) og (S) er i samme plan, som vist i øvelse 3. Finn ligningen til planet som inneholder dem.
Løsning
Punktene A, B, C definerer det planet fullstendig, men vi vil pålegge at ethvert punkt X av koordinatene (x, y, z) tilhører det samme.
X - A: (x-1, y -1, z - 1) => ØKS= (x-1, y -1, z - 1)
B - A: (3-1, 0 -1, 1 - 1) => AB= (2, -1, 0)
C - A: (0-1, 1/2 -1, -1 - 1) => AC= (-1, -1/2, -2)
For at X skal tilhøre planet definert av A, B, C og hvor linjene (R) og (S) er inneholdt, er det nødvendig at determinanten dannes i sin første rad av komponentene i ØKS, i det andre av de av AB og i den tredje av de av AC:
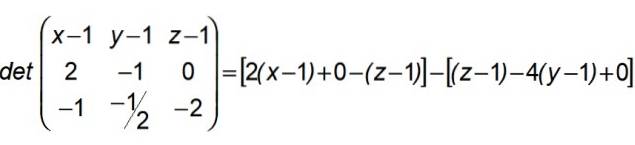
Etter dette resultatet grupperer vi på denne måten:
2 (x-1) + 4 (y-1) -2 (z-1) = 0
Og umiddelbart ser du at det kan skrives om slik:
x - 1 + 2y - 2 - z + 1 = 0
Derfor er x + 2y - z = 2 ligningen til planet som inneholder linjene (R) og (S).
Referanser
- Fleming, W. 1989. Precalculus Mathematics. Prentice Hall PTR.
- Kolman, B. 2006. Lineær algebra. Pearson Education.
- Leal, J. M. 2005. Plane Analytical Geometry. Mérida - Venezuela: Redaksjonelt Venezolana C. A.
- Navarro, Rocio. Vektorer. Gjenopprettet fra: books.google.co.ve.
- Pérez, C. D. 2006. Forberegning. Pearson Education.
- Prenowitz, W. 2012. Grunnleggende begreper for geometri. Rowman & Littlefield.
- Sullivan, M. 1997. Precalculus. Pearson Education.



Ingen har kommentert denne artikkelen ennå.