Hva er modul for skjær, stivhet eller skjær? (Øvelser løst)

De skjæremodul beskriver responsen til et materiale på påføring av en skjærspenning som deformerer det. Andre ofte brukte navn på skjærmodul er skjærmodul, skjærmodul, tverrelastisitet eller tangensiell elastisitet..

Når spenningene er små, er deformasjonene proporsjonale med dem, ifølge Hookes lov, hvor skjærmodulen er konstanten av proporsjonaliteten. Derfor:

Skjærmodul = Skjærspenning / belastning

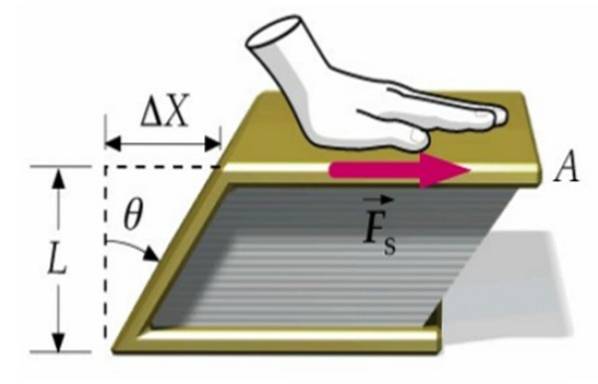
Anta at den ene kraften blir påført omslaget til en bok, den andre er festet på overflaten av bordet. På denne måten beveger ikke boken seg som helhet, men deformeres når det øvre omslaget beveger seg i forhold til det nedre. Δx.

Boken går fra å ha et rektangulært tverrsnitt til et parallellogramformet snitt, som vi ser på bildet ovenfor.

Være:

τ = F / A

Skjærspenningen eller spenningen, det å være F størrelsen på den påførte kraften og TIL området det virker på.

Deformasjonen forårsaket er gitt av kvotienten:

δ = Δx / L

Derfor er skjærmodulen, som vi vil betegne som G:

Og siden Δx / L ikke har noen dimensjoner, er enhetene til G de samme som skjærspenningen, som er forholdet mellom kraft og areal..

I det internasjonale systemet for enheter er disse enhetene Newton / kvadratmeter eller pascal, forkortet Pa. Og i angelsaksiske enheter er det pund / kvadrat tomme, forkortet psi.

Artikkelindeks

• 1 Skjæremodul for forskjellige materialer
  • 1.1 Eksperimentell måling av skjærmodul
  • 1.2 Hvordan finne ut G?
• 2 Øvelser med løsning
  • 2.1 - Øvelse 1
  • 2.2 - Øvelse 2
• 3 Referanser

Skjæremodul for forskjellige materialer

Under påvirkning av skjærkrefter som de som er beskrevet, gir gjenstandene en motstand som ligner på boken, der de indre lagene glir. Denne typen deformasjon kan bare forekomme i faste legemer, som har tilstrekkelig stivhet til å motstå deformasjon..

På den annen side tilbyr ikke væsker denne typen motstand, men de kan gjennomgå volumdeformasjoner.

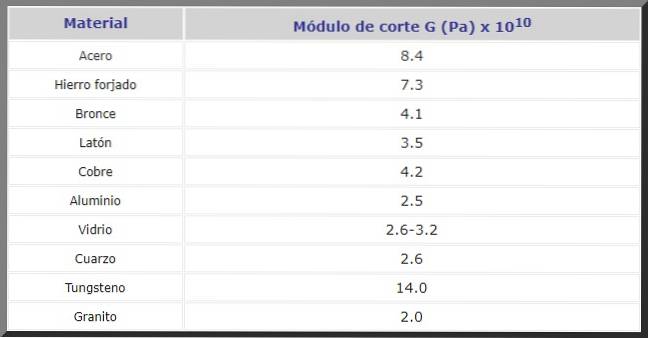
Nedenfor er G in Pa skjæremodul for forskjellige materialer som ofte brukes i konstruksjon og produksjon av maskiner og reservedeler av alle slag:

Eksperimentell måling av skjærmodul

For å finne verdien av skjærmodulen, må prøver av hvert materiale testes og deres respons på påføring av skjærspenning undersøkes..

Prøven er en stang laget av materialet, med radius R og lengde L kjent, som er festet i den ene enden, mens den andre er koblet til akselen til en remskive som er fri til å rotere.

Remskiven er bundet med et tau, i den frie enden som det henges en vekt som utøver en kraft F på stangen gjennom tauet. Og denne kraften produserer igjen et øyeblikk M på stangen, som deretter roterer en liten vinkel θ.

Et diagram over samlingen kan sees i følgende figur:

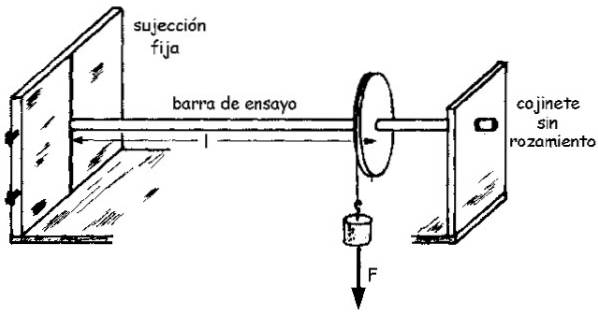
Øyeblikkets størrelse M, som vi betegner som M (ingen fet skrift) er relatert til den roterte vinkelen θ gjennom skjærmodulen G i henhold til følgende ligning (utledet av en enkel integral):

Siden størrelsen på øyeblikket er lik produktet av modulen med kraften F og radien til remskiven R_s:

M = F.R_s

Og styrke er vekten som henger W, deretter:

M = W.R_s

Erstatter i ligningen for øyeblikkets størrelse:

Det er forholdet mellom vekt og vinkel:

Hvordan finne G?

Dette forholdet mellom variablene W Y θ er lineær, så de forskjellige vinklene som produseres ved å henge forskjellige vekter måles.

Vekt- og vinkelparene er plottet på grafpapir, den beste linjen som passerer gjennom eksperimentelle punkter er montert, og hellingen beregnes. m av linjen.

Øvelser med løsning

- Øvelse 1

En stang 2,5 meter lang og radius 4,5 mm er festet i den ene enden. Den andre er koblet til en radius på 75 cm med en hengende vekt på 1,3 kg. Den roterte vinkelen er 9,5 º.

Med disse dataene blir det bedt om å beregne stangens skjærmodul G.

Løsning

Fra ligningen:

G er ryddet:

Og verdiene gitt i uttalelsen er erstattet, og pass på å uttrykke alle dataene i det internasjonale systemet for enheter SI:

R = 4,5 mm = 4,5 x 10 ^-3 m

R_s = 75 cm = 0,075

Å gå fra kilo (som faktisk er kilo - kraft) til newton multipliseres med 9,8:

W = 1,3 kg-kraft = 1,3 x 9,8 N = 12,74 N.

Og til slutt må gradene være i radianer:

9,5 º = 9,5 x2π / 360 radianer = 0,1665 radianer.

Med alt dette har du:

= 2237 x 10¹⁰ Pa

- Øvelse 2

En terning laget av gel har en side på 30 cm. En av ansiktene er faste, men samtidig påføres en parallell kraft på 1 N på det motsatte ansiktet, som takket være den beveger seg 1 cm (se eksemplet på boka i figur 1).

Det bedes beregne med disse dataene:

a) Størrelsen på skjærspenningen

b) Sil δ

c) Verdien av skjærmodulen

Løsning til

Skjærspenningens størrelse er:

τ = F / A

Med:

A = side^to = (30 x 10^-to cm)^to = 0,09 m^to

Derfor:

τ = 1 N / 0,09 m^to = 11,1 Pa

Løsning b

Stamme er ingen ringere enn verdien av δ, gitt av:

δ = Δx / L

Forskyvningen av ansiktet som utsettes for kraften er 1 cm, deretter:

5 = 1/30 = 0,0333

Løsning c

Skjærmodulen er kvotienten mellom skjærspenningen og belastningen:

G = Skjærspenning / belastning

Derfor:

G = 11,1 Pa / 0,033 = 336,4 Pa

Referanser

1. Beer, F. 2010. Mekanikk av materialer. McGraw Hill. 5. Utgave.
2. Franco García, A. Solid Rigid. Skjærmodulmåling. Gjenopprettet fra: sc.ehu.es.
3. Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. Sjette. Ed prentice hall.
4. Resnick, R. (1999). Fysisk. Vol. 1. 3. utgave på spansk. Compañía Editorial Continental S.A. av C.V.
5. Universitetet i Valladolid. Institutt for fysikk av kondensert materiale. Utvalg av problemer. Gjenopprettet fra: www4.uva.es.