Hva er lineær hastighet? (Med øvelser løst)

De lineær hastighet det er definert som det som alltid er tangensielt for banen som partikkelen følger, uavhengig av form. Hvis partikkelen alltid beveger seg i en rettlinjet bane, er det ikke noe problem å forestille seg hvordan hastighetsvektoren følger denne rette linjen.

Imidlertid utføres generelt bevegelsen på en vilkårlig formet kurve. Hver del av kurven kan modelleres som om den var en del av en sirkel med radius til, som på hvert punkt er tangent til stien som følges.

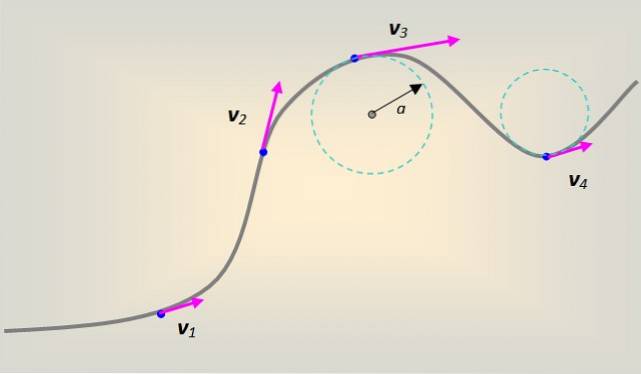
I dette tilfellet følger den lineære hastigheten kurven tangentielt og til enhver tid på hvert punkt av den..

Matematisk er den øyeblikkelige lineære hastigheten avledet av posisjonen med hensyn til tid. Være r posisjonsvektoren til partikkelen på et øyeblikk t, så er den lineære hastigheten gitt av uttrykket:

v = r'(t) = dr / dt

Dette betyr at den lineære hastigheten eller tangentiell hastighet, som det også ofte kalles, ikke er noe annet enn endringen i posisjon med hensyn til tid..

Artikkelindeks

• 1 Lineær hastighet i sirkulær bevegelse
  • 1.1 Lineær hastighet, vinkelhastighet og sentripetal akselerasjon
  • 1.2 -Løst øvelse 1 
  • 1.3 -Løst øvelse 2
• 2 Referanser

Lineær hastighet i sirkulær bevegelse

Når bevegelsen er på en omkrets, kan vi gå ved siden av partikkelen på hvert punkt og se hva som skjer i to helt spesielle retninger: en av dem er den som alltid peker mot sentrum. Dette er adressen radial.

Den andre viktige retningen er den som passerer omkretsen, dette er retningen tangensiell og lineær hastighet har det alltid.

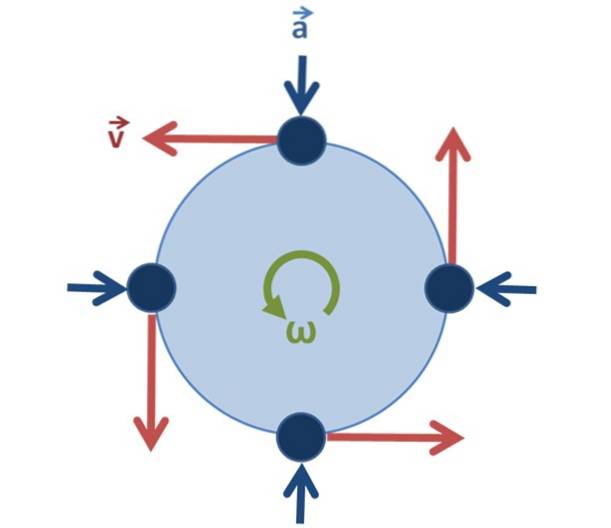
Når det gjelder ensartet sirkulær bevegelse, er det viktig å innse at hastigheten ikke er konstant, siden vektoren endrer retning når partikkelen roterer, men dens modul (størrelsen på vektoren), som er hastigheten, ja forblir uendret.

For denne bevegelsen er posisjonen som en funksjon av tid gitt av s (t), hvor s er han bueløp Y t Det er tiden. I så fall blir øyeblikkelig hastighet gitt av uttrykket v = ds / dt og det er konstant.

Hvis størrelsen på hastigheten også varierer (vi vet allerede at retningen alltid gjør, ellers kunne ikke mobilen svinge), står vi overfor en variert sirkelbevegelse, der mobilen, i tillegg til å snu, kan bremse eller akselerere.

Lineær hastighet, vinkelhastighet og sentripetal akselerasjon

Partikkelens bevegelse kan også sees fra synspunktet til feid vinkel, i stedet for å gjøre det fra buegangen. I et slikt tilfelle snakker vi om vinkelhastighet. For en bevegelse på en radius av omkretsen R, det er et forhold mellom lysbue (i radianer) og vinkel:

s = R θ

Avledning med hensyn til tid på begge sider:

ds / dt = R (dθ/ dt)

Kaller derivatet av θ med hensyn til t Hva vinkelhastighet og betegner det med den greske bokstaven ω "omega", har vi dette forholdet:

v = ωR

Sentripetal akselerasjon

All sirkulær bevegelse har sentripetal akselerasjon, som alltid er rettet mot sentrum av omkretsen. Hun sørger for at hastigheten endres for å bevege seg med partikkelen når den roterer.

Sentripetal akselerasjon til_c eller til_R peker alltid mot sentrum (se figur 2) og er relatert til lineær hastighet slik:

til_c = v^to / R

Og med vinkelhastigheten som:

til_c = (ωR)^to / R = ω^toR

For jevn sirkelbevegelse, posisjonen s (t) er av formen:

s (t) = så + vt

Videre må den varierte sirkulære bevegelsen ha en komponent av akselerasjon som kalles tangentiell akselerasjon til_T, som handler om å endre størrelsen på lineær hastighet. Ja til_T  det er konstant, stillingen er:

s (t) = s_eller + v_ellert + ½ a_Tt^to

Med v_eller som utgangshastighet.

Løste problemer med lineær hastighet

De løste øvelsene hjelper deg med å avklare riktig bruk av konseptene og ligningene gitt ovenfor..

-Løst øvelse 1 

Et insekt beveger seg på en halvsirkel med radius R = 2 m, fra hvile ved punkt A mens den øker sin lineære hastighet, med en hastighet på p m / s^to. Finn: a) Etter hvor lenge den når punkt B, b) Lineær hastighetsvektor i det øyeblikket, c) Akselerasjonsvektor i det øyeblikket.

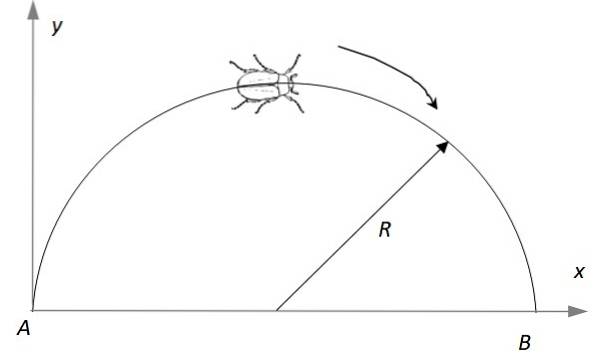
Løsning

a) Uttalelsen indikerer at den tangentielle akselerasjonen er konstant og er lik π m / s^to, da er det gyldig å bruke ligningen for jevnt variert bevegelse:

s (t) = s_eller + v_ellert + ½ a_T.t^to

Med s_eller = 0 og v_eller = 0:

s (t) = ½ a_T.t^to

s = πR (Halv lengde på omkretsen)

t = (2. πR /til_T) ^½ s = (2π.2 / π)^½s = 2 s

b) v (t) = v_eller + til_T. t = 2π m / s

Når det er punkt B, peker den lineære hastighetsvektoren i vertikal retning nedover i retningen (-Y):

v (t) = 2π m / s(-Y)

c) Vi har allerede tangentiell akselerasjon, sentripetal akselerasjon mangler for å ha hastighetsvektoren til:

til_c = v^to / R = (2π)^to / 2 m / s^to = 2π^to m / s^to

til = a_c (-x) + a_T (-Y) = 2π^to(-x) + π (-Y) m / s^to

-Trening løst 2

En partikkel roterer i en sirkel med en radius på 2,90 m. I et bestemt øyeblikk er akselerasjonen 1,05 m / s^to i en slik retning at den danner 32º med sin bevegelsesretning. Finn dens lineære hastighet ved: a) Dette øyeblikket, b) 2 sekunder senere, forutsatt at den tangentielle akselerasjonen er konstant.

Løsning

a) Bevegelsesretningen er nettopp den tangensielle retningen:

til_T = 1,05 m / s^to . cos 32º = 0,89 m / s^to ; til_C = 1,05 m / s^to . sin 32º = 0,56 m / s^to

Hastigheten tømmes fra til_c = v^to / R Hva:

v = (R.a_c)^1/2  = 1,27 m / s

b) Følgende ligning er gyldig for jevnt varierte bevegelser: v = v_eller + til_Tt = 1,27 + 0,89, 2^to m / s = 4,83 m / s

Referanser

1. Bauer, W. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill. 84-88.
2. Figueroa, D. Physics Series for Sciences and Engineering. Volum 3. Utgave. Kinematikk. 199-232.
3. Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. 6^th... Ed Prentice Hall. 62-64.
4. Relativ bevegelse. Gjenopprettet fra: courses.lumenlearning.com
5. Wilson, J. 2011. Fysikk 10. Pearson Education. 166-168.