Hva er en icosagon? Egenskaper og egenskaper

EN icosagon eller isodecagon er en polygon som har 20 sider. En polygon er en plan figur dannet av en endelig sekvens av linjesegmenter (mer enn to) som omslutter en region av planet.

Hvert linjesegment kalles en side, og skjæringspunktet mellom hvert sidepar kalles toppunkt. I henhold til antall sider får polygonene spesielle navn.

De vanligste er trekanten, firkantet, femkantet og sekskantet, som har henholdsvis 3, 4, 5 og 6 sider, men kan bygges med antall sider du vil ha.

Kjennetegn ved en ikosagon

Nedenfor er noen kjennetegn ved polygoner og deres anvendelse i en ikonikon.

1- Klassifisering

En ikosagon, som er en polygon, kan klassifiseres som vanlig og uregelmessig, hvor ordet regelmessig refererer til det faktum at alle sidene har samme lengde og innvendige vinkler alle måler det samme; ellers sies det at ikosagonen (polygon) er uregelmessig.

2- Isodecagon

Den vanlige icosagon kalles også en vanlig isodecagon, for å få en vanlig icosagon er det du må gjøre å halvere (dele i to like store deler) hver side av en vanlig decagon (10-sidet polygon).

3- Omkrets

For å beregne omkretsen "P" til en vanlig polygon multipliseres antall sider med lengden på hver side.

I det spesielle tilfellet med en ikosagon er omkretsen lik 20xL, hvor "L" er lengden på hver side.

Hvis du for eksempel har en vanlig ikon med en 3 cm side, er omkretsen lik 20x3cm = 60cm.

Det er klart at, hvis isogonen er uregelmessig, kan formelen ovenfor ikke brukes.

I dette tilfellet må de 20 sidene legges til separat for å oppnå omkretsen, det vil si at omkretsen "P" er lik ∑Li, med i = 1,2,…, 20.

4- Diagonaler

Antall diagonaler "D" som en polygon har er lik n (n-3) / 2, hvor n representerer antall sider.

Når det gjelder en ikosagon, følger det at den har D = 20x (17) / 2 = 170 diagonaler.

5- Summen av de indre vinklene

Det er en formel som hjelper til med å beregne summen av de indre vinklene til en vanlig polygon, som kan brukes på en vanlig icosagon.

Formelen består i å trekke 2 fra antall sider på polygonen og deretter multiplisere dette tallet med 180º.

Måten denne formelen oppnås på er at vi kan dele en polygon med n sider i n-2 trekanter, og ved å bruke det faktum at summen av de indre vinklene til en trekant er 180 °, får vi formelen.

Følgende bilde illustrerer formelen for en vanlig enegon (9-sidig polygon).

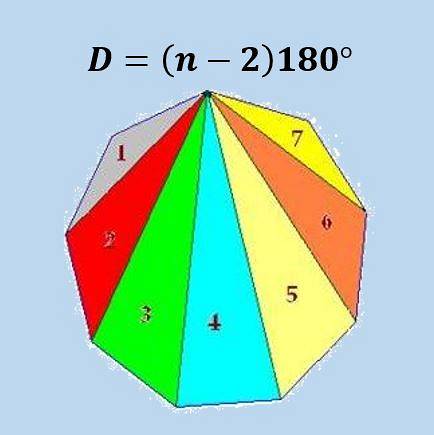
Ved å bruke den ovennevnte formelen oppnås det at summen av de indre vinklene til en hvilken som helst ikosagon er 18 × 180º = 3240º eller 18π.

6- Område

For å beregne arealet til en vanlig polygon er det veldig nyttig å kjenne begrepet apothem. Apotemet er en vinkelrett linje som går fra midten av den vanlige polygonen til midtpunktet på en av sidene.

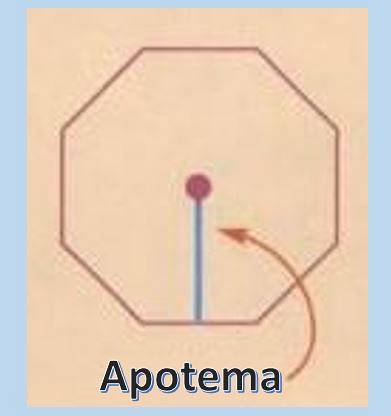
Når lengden på apotemet er kjent, er området til en vanlig polygon A = Pxa / 2, hvor "P" representerer omkretsen og "a" apotemet..

Når det gjelder en vanlig ikosagon, er arealet A = 20xLxa / 2 = 10xLxa, hvor "L" er lengden på hver side og "a" er apotemet.

På den annen side, hvis du har en uregelmessig polygon med n sider, for å beregne arealet, dele polygonen i n-2 kjente trekanter, og deretter beregne arealet til hver av disse n-2-trekanter og til slutt legge til alle disse områdene.

Metoden beskrevet ovenfor er kjent som triangulering av en polygon.

Referanser

1. C., E. Á. (2003). Geometrielementer: med mange øvelser og kompassgeometri. University of Medellin.
2. Campos, F. J., Cerecedo, F. J., og Cerecedo, F. J. (2014). Matematikk 2. Grupo Redaksjonell Patria.
3. Freed, K. (2007). Oppdag polygoner. Referanseutdanningsfirma.
4. Hendrik, v. M. (2013). Generelle polygoner. Birkhäuser.
5. IGER. (s.f.). Matematikk Første semester Tacaná. IGER.
6. jrgeometry. (2014). Polygoner. Lulu Press, Inc..
7. Mathivet, V. (2017). Kunstig intelligens for utviklere: konsepter og implementering i Java. ENI-utgaver.
8. Miller, Heeren & Hornsby. (2006). Matematikk: resonnement og applikasjoner 10 / e (Tiende utgave utg.). Pearson Education.
9. Oroz, R. (1999). Ordbok for det spanske språket. University Publishing House.
10. Patiño, M. d. (2006). Matematikk 5. Redaksjonell Progreso.
11. Rubió, M. d.-M. (1997). Formene for byvekst. Univ. Politèc. fra Catalunya.