
Hvilke typer integraler er det?

De typer integraler som vi finner i beregningen er de ubestemte integralene og de bestemte integralene. Selv om bestemte integraler har mange flere applikasjoner enn ubestemte integraler, er det nødvendig å først lære å løse ubestemte integraler..
En av de mest attraktive anvendelsene av bestemte integraler er beregningen av volumet til et solid revolusjon. Begge typer integraler har de samme linearitetsegenskapene, og integrasjonsteknikkene avhenger ikke av typen integral.
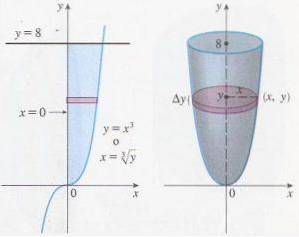
Men til tross for at de er veldig like, er det en hovedforskjell; i den første typen integral er resultatet en funksjon (som ikke er spesifikk) mens i den andre typen er resultatet et tall.
Grunnleggende typer integraler
Verden av integraler er veldig bred, men innenfor den kan vi skille mellom to grunnleggende typer integraler, som har stor anvendelighet i hverdagen..
1- Ubestemte integraler
Hvis F '(x) = f (x) for alle x i domenet til f, sier vi at F (x) er en antiderivativ, en primitiv eller en integral av f (x).
På den annen side, la oss observere at (F (x) + C) '= F' (x) = f (x), noe som innebærer at integriteten til en funksjon ikke er unik, siden vi gir forskjellige verdier til konstant C vil vi oppnå forskjellige antiderivativer.
Av denne grunn kalles F (x) + C den ubestemte integralen til f (x) og C kalles integrasjonskonstanten, og vi skriver det som følger
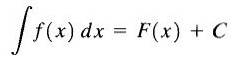
Som vi kan se, er den ubestemte integralen til funksjonen f (x) en familie av funksjoner.
For eksempel, hvis du vil beregne den ubestemte integralen til funksjonen f (x) = 3x², må du først finne et antiderivativ av f (x).
Det er lett å se at F (x) = x³ er antiderivativ, siden F '(x) = 3x². Derfor kan det konkluderes med at
∫f (x) dx = ∫3x²dx = x³ + C.
2 - Definitive integraler
La y = f (x) være en reell, kontinuerlig funksjon i et lukket intervall [a, b] og la F (x) være et antivirativt forhold til f (x). Den bestemte integralen av f (x) mellom grensene a og b kalles tallet F (b) -F (a), og betegnes som følger
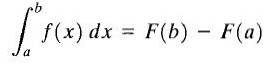
Formelen vist ovenfor er bedre kjent som "The Fundamental Theorem of Calculus." Her kalles "a" den nedre grensen og "b" kalles den øvre grensen. Som du kan se, er den definitive integralen til en funksjon et tall.
I dette tilfellet, hvis vi beregner den bestemte integralen av f (x) = 3x² i intervallet [0,3], vil vi få et tall.
For å bestemme dette tallet velger vi F (x) = x³ som antiderivativ for f (x) = 3x². Deretter beregner vi F (3) -F (0) som gir oss resultatet 27-0 = 27. Avslutningsvis er den bestemte integralen av f (x) på intervallet [0,3] 27.
Det kan bemerkes at hvis G (x) = x³ + 3 er valgt, så er G (x) et antiderivativ av f (x) forskjellig fra F (x), men dette påvirker ikke resultatet siden G (3) - G (0) = (27 + 3) - (3) = 27. Av denne grunn vises ikke integrasjonskonstanten i de bestemte integralene.
En av de mest nyttige applikasjonene for denne typen integral er at den gjør det mulig å beregne arealet (volumet) til en plan figur (av et solid revolusjon), etablere egnede funksjoner og grenser for integrering (og en rotasjonsakse).
Innenfor de definerte integralene kan vi finne forskjellige utvidelser av den, for eksempel linjeintegraler, overflateintegraler, upassende integraler, flere integraler, blant andre, alle med veldig nyttige applikasjoner innen vitenskap og ingeniørfag..
Referanser
- Casteleiro, J. M. (2012). Er det enkelt å integrere? Selvstudiehåndbok. Madrid: ESIC.
- Casteleiro, J. M., og Gómez-Álvarez, R. P. (2002). Integrert kalkulator (Illustrert utg.). Madrid: ESIC-redaksjon.
- Fleming, W., & Varberg, D. E. (1989). Precalculus matematikk. Prentice Hall PTR.
- Fleming, W., & Varberg, D. E. (1989). Precalculus matematikk: en problemløsende tilnærming (2, Illustrert utg.). Michigan: Prentice Hall.
- Kishan, H. (2005). Integral Calculus. Atlantic Publishers & Distributors.
- Purcell, E. J., Varberg, D., og Rigdon, S. E. (2007). Beregning (9. utg.). Prentice hall.


Ingen har kommentert denne artikkelen ennå.