Skrå karakteristiske linjer, ligninger og eksempler

De skrå linjer De er de som er skrå, enten med hensyn til en flat overflate eller til en annen rett som indikerer en bestemt retning. Som et eksempel kan du se på de tre linjene tegnet i et plan som vises i følgende figur.

Vi kjenner deres respektive relative posisjoner fordi vi sammenligner dem med en referanselinje, som vanligvis er X-akse betegner det horisontale.

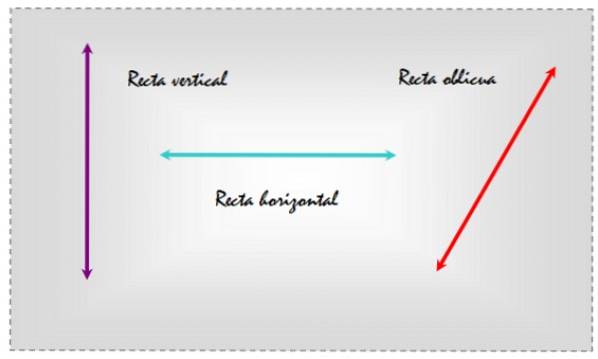
På denne måten velger du det horisontale som referanse, linjen til venstre er loddrett, den i midten er horisontal og den til høyre er skrå, siden den er tilbøyelig i forhold til hverdagsreferanselinjene..

Nå opptar linjene som er på samme plan, som overflaten på papiret eller skjermen, forskjellige relative posisjoner avhengig av om de krysser hverandre eller ikke. I det første tilfellet er de sekante linjer, mens i det andre er de parallelle.

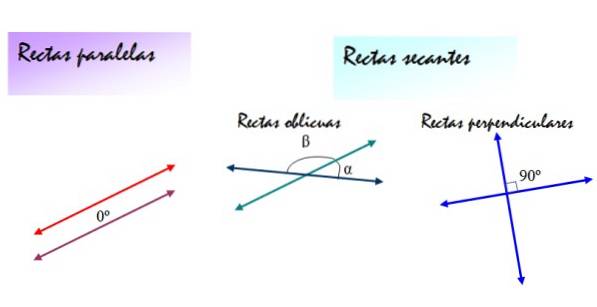
På den annen side kan sekantlinjene være skrå linjer eller vinkelrette linjer. I begge tilfeller er linjens skråninger forskjellige, men de skrå linjene danner vinkler α og β mellom dem, forskjellig fra 90 °, mens vinklene bestemt av de vinkelrette linjene alltid er 90 °..

Følgende figur oppsummerer disse definisjonene:

Artikkelindeks

• 1 ligninger
  • 1.1 Ligning av linjen i planet
• 2 Eksempler på skrå linjer
  • 2.1 Lysstråler
  • 2.2 Linjer som ikke er i samme plan
• 3 Referanser

Ligninger

For å kjenne de relative posisjonene til linjene i planet, er det nødvendig å kjenne vinkelen de danner med hverandre. Merk at linjene er:

Parallell: hvis de har samme skråning (samme retning) og aldri krysser hverandre, er poengene deres like langt fra hverandre.

Sammentreff: når alle punktene faller sammen og derfor har samme skråning, men avstanden mellom punktene er null.

Tørking: hvis bakkene er forskjellige, varierer avstanden mellom punktene og krysset er et enkelt punkt.

Så en måte å vite om to linjer i planet er sekant eller parallell, er gjennom skråningen. Kriteriene for parallellitet og vinkelrett på linjene er følgende:

La L være to linjer₁ og jeg_to tilhører et fly, hvis skråninger er henholdsvis m₁ og M_to. Disse linjene er parallelle hvis m₁ = m_to og er vinkelrett når m₁= -1 / m_to

Hvis ingen av de foregående kriteriene er oppfylt, hvis vi kjenner bakken til to linjer i planet, konkluderer vi med at linjene er skrå. Å vite to punkter på en linje, blir hellingen beregnet umiddelbart, som vi vil se i neste avsnitt.

Det er mulig å finne ut om to linjer er sekante eller parallelle ved å finne skjæringspunktet deres, løse ligningssystemet som de danner: hvis det er en løsning, er de sekanter, hvis det ikke er noen løsning, er de parallelle, men hvis løsningene er uendelig, linjene er sammenfallende.

Dette kriteriet informerer oss imidlertid ikke om vinkelen mellom disse linjene, selv om de krysser hverandre.

For å kjenne vinkelen mellom linjene, trengs to vektorer eller Y v som tilhører hver enkelt av dem. Dermed er det mulig å kjenne vinkelen de danner ved hjelp av det skalære produktet til vektorene, definert på denne måten:

eller•v =u.v.cos α

Ligning av linjen i flyet

En linje i det kartesiske planet kan vises på flere måter, for eksempel:

-Skråningsavskjæringsform: Ja m er skråningen på linjen og b er skjæringspunktet mellom linjen og den vertikale aksen, ligningen på linjen er y = mx + b.

-Generell ligning for en rett linje: Ax + By + C = 0, hvor m = A / B er skråningen.

I det kartesiske planet er de vertikale og horisontale linjene spesielle tilfeller av linjens ligning.

-Vertikale linjer: x = a

-Horisontale linjer: y = k

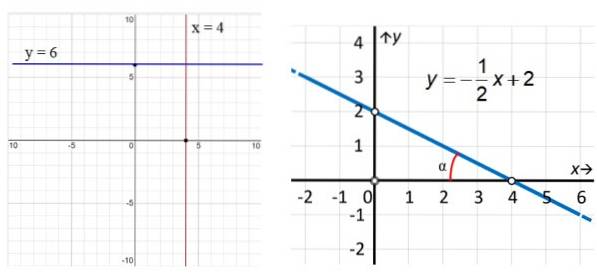
I eksemplene i figur 3 har den vertikale røde linjen ligning x = 4, mens linjen parallell med x-aksen (blå) har ligningen y = 6. Når det gjelder linjen til høyre, ser vi at den er skrå og til finn ligningen vi bruker punktene uthevet i figuren: (0,2) og (4,0) på denne måten:

m = (og_to - Y₁) / (x_to - x₁) = (2 - 0) / (0 - 4) = - ½

Skjæringen av denne linjen med den vertikale aksen er y = 2, som det fremgår av grafen. Med denne informasjonen:

y = (-½) x + 2

Det er enkelt å bestemme hellingsvinkelen i forhold til x-aksen. Jeg føler det:

α = arctg (2/4) = 26,6º

Derfor er den positive vinkelen fra x-aksen til linjen: 180º - 26,6º = 153,4º

Eksempler på skrå linjer

Skrå linjer vises mange steder, det er et spørsmål om å være oppmerksom på å finne dem i arkitektur, sport, ledningsnett for strømforsyning, rør og mange flere steder. I naturen er også skrå linjer til stede, som vi vil se nedenfor:

Lysstråler

Sollys beveger seg i en rett linje, men jordens avrundede form påvirker hvordan sollys treffer overflaten..

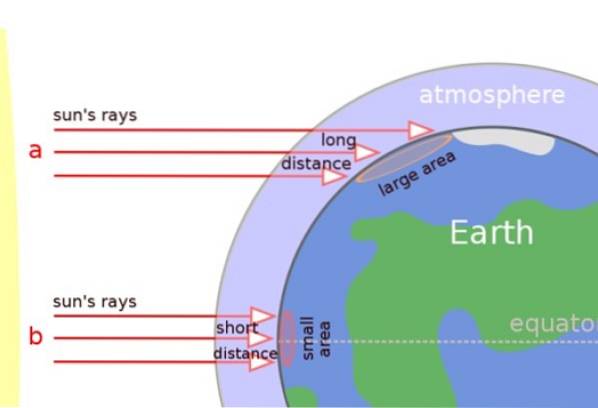
På bildet nedenfor kan vi tydelig se at solstrålene slår vinkelrett i tropiske regioner, men i stedet kommer skrått til overflaten i tempererte områder og ved polene..

Dette er grunnen til at solstrålene beveger seg lengre avstand gjennom atmosfæren, og varmen spres også over en større overflate (se figur). Resultatet er at områdene nær stolpene er kaldere.

Linjer som ikke er i samme plan

Når to linjer ikke er i samme plan, kan de fremdeles være skrå eller vridd, som de også er kjent. I dette tilfellet er deres regissørvektorer ikke parallelle, men siden de ikke tilhører samme plan, krysser ikke disse linjene.

For eksempel er linjene i figur 6 til høyre tydelig på forskjellige plan. Hvis du ser på dem ovenfra, kan du se at de virkelig krysser hverandre, men de har ikke noe felles. Til høyre ser vi hjulene på sykkelen, hvis eiker ser ut til å krysse når de sees forfra.

Referanser

1. Geometri. Direktørvektor av en linje. Gjenopprettet fra: juanbragado.es.
2. Larson, R. 2006. Calculus with Analytical Geometry. 8. plass. Utgave. Mcgraw hill.
3. Matematikk er et spill. Linjer og vinkler. Gjenopprettet fra: juntadeandalucia.es.
4. Rette linjer som krysser hverandre. Gjenopprettet fra: profesoraltuna.com.
5. Villena, M. Analytisk geometri i R3. Gjenopprettet fra: dspace.espol.edu.ec.