
Bravais nettverk konsept, egenskaper, eksempler, øvelser
De Bravais garn De er settet med fjorten tredimensjonale enhetsceller der atomene til en krystall kan være plassert. Disse cellene består av et tredimensjonalt arrangement av punkter som danner en grunnleggende struktur som gjentas periodisk i de tre romlige retningene..
Opprinnelsen til denne betegnelsen for de grunnleggende krystallinske strukturene kommer fra 1850, da Auguste Bravais viste at det bare er 14 mulige tredimensjonale basiske enhetsceller.

Settet med 14 Bravais-nettverk er delt inn i syv grupper eller strukturer i henhold til cellens geometri, disse syv gruppene er:
1- Kubikk
2- Tetragonal
3- Orthorhombic
4- Trigonal-sekskantet
5- Monoklinikk
6- Triklinikk
7- Trigonal
Hver av disse strukturene definerer en enhetscelle, dette er den minste delen som bevarer det geometriske arrangementet av atomene i krystallet..
Artikkelindeks
- 1 Kjennetegn ved Bravais-nettverk
- 1.1 Kubiske nettverk
- 2 Eksempler
- 2.1 - Jern
- 2.2 - Kobber
- 2.3 - Edle perler
- 2.4 Topas
- 3 Løst øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 3.3 Øvelse 3
- 4 Referanser
Kjennetegn ved Bravais-nettverk
De fjorten Bravais-nettverk, som nevnt ovenfor, er delt inn i syv grupper. Men hver av disse gruppene har sine enhetsceller med sine karakteristiske parametere som er:
1- Nettverksparameteren (a, b, c)
2- Antall atomer per celle
3- Forholdet mellom nettverksparameter og atomradius
4- Koordineringsnummer
5- Pakningsfaktor
6- mellomrom
7- Gjennom oversettelser langs vektorene a, b, c gjentas krystallstrukturen.
Kubiske nettverk
Den består av det enkle kubiske eller kubiske nettverket P, ansiktssentrert kubisk nettverk eller kubisk nettverk F og det kroppssentrerte kubiske nettverket eller kubiske nettverket I.
Alle kubiske nettverk har alle tre nettverksparametere tilsvarer retninger x, y, z med samme verdi:
a = b = c
Kubisk nettverk P
Det skal bemerkes at atomer er representert av kuler hvis sentre er i toppunktene til den kubiske enhetscellen P.
I tilfelle av det kubiske gitteret P antall atomer per celle er 1, fordi bare en åttendedel av atomet i hvert toppunkt er inne i enhetscellen, så 8 * ⅛ = 1.
De koordineringsnummer angir antall atomer som er nære naboer i krystallgitteret. For kubikkgitteret P er koordinasjonsnummeret 6.
Kubikknettverk I
I denne typen nettverk, i tillegg til atomene i kubenes toppunkt, er det et atom i midten av kuben. Så antall atom per celle enhet i kubisk gitter P er 2 atomer.

Kubikknettverk F
Det er det kubiske gitteret som, i tillegg til atomene i toppunktene, har et atom i midten av ansiktet til hver kube. De antall atomer per celle er 4, siden hvert av de seks atomer i ansiktet har halvparten inne i cellen, det vil si 6 * ½ = 3 pluss 8 * ⅛ = 1 i toppunktene.

Sekskantet nett
I dette tilfellet er enhetscellen et rett prisme med en sekskantet base. Sekskantede nettverk har alle tre nettverksparametere tilsvarende oppfyller følgende forhold:
a = b ≠ c
Vinkelen mellom vektor a og b er 120º, som vist i figuren. Mens mellom vektorene a og c, så vel som mellom b og c, dannes rette vinkler.

De antall atomer per celle beregnes som følger:
- I hver av de to basene til det sekskantede prismen er det 6 atomer ved de seks toppunktene. Hvert av disse atomene opptar ⅙ av enhetscellen.
- I midten av hver av de to sekskantede basene er det 1 atom som opptar 1/2 enhetscelle.
- På de seks sideflatene til det sekskantede prismen er det 3 atomer som hver okkuperer ⅔ av enhetscellen, og 3 atomer som hver okkuperer ⅓ av enhetscellevolumet.
(6 x ⅙) x 2 + ½ x 2 + ⅔ x 3 + ⅓ x 3 = 6
Forholdet mellom gitterparametrene a og b med atomradiusen R under antagelse om at alle atomene har samme radius og er i kontakt er:
a / R = b / R = 2
Eksempler
Metaller er de viktigste eksemplene på krystallinske strukturer og også de enkleste fordi de generelt bare består av en type atom. Men det er andre ikke-metalliske forbindelser som også danner krystallinske strukturer, som diamant, kvarts og mange andre..
- Jernet
Jern har en enkelt kubisk enhetscelle med gitter eller kantparameter a = 0,297 nm. I 1 mm er det 3,48 x 10 ^ 6 enhetsceller.
- Kobber
Den har en ansiktssentrert kubisk krystallinsk struktur, som bare består av kobberatomer..
- Edle perler
Edle edelstener er krystallinske strukturer av i utgangspunktet den samme forbindelsen, men med små porsjoner av urenheter som ofte er ansvarlige for fargen..
Diamant
Den består utelukkende av karbon og inneholder ikke urenheter, og det er derfor den er fargeløs. Diamanten har kubisk krystallstruktur (isometrisk-heksoktaedrisk) og er det vanskeligste kjente materialet.
Kvarts
Den består av silisiumoksyd, den er vanligvis fargeløs eller hvit. Den krystallinske strukturen er trigonal-trapezohedral.
Rubin
Den består av aluminiumoksid med kromurenheter som gir den sin karakteristiske røde farge. Skjema a sekskantet krystallgitter.
Safir
Det er også en krystall av aluminiumoksid, men med urenheter av titan og jern, som er ansvarlig for den blå fargen i forskjellige nyanser. Som rubinen har sekskantet struktur.
Jade
Edelsten generelt grønn i fargen, har monoklinisk struktur og består av jern-magnesium-kalsiumsilikat.
Topaz
Den er fargeløs med en ortorhombisk struktur aluminiumfluorid-hydroksid-silikat.
Løst øvelser
Øvelse 1
Finn forholdet mellom gitterparameteren og atomradiusen for et kubisk gitter F.
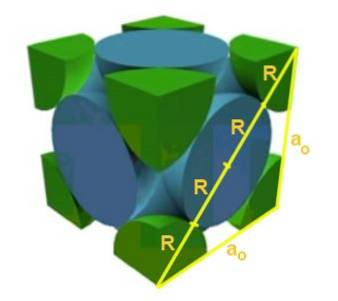
Løsning: For det første antas det at atomene er representert som kuler hele radius R i "kontakt" med hverandre, som vist i figuren. En rett trekant dannes der det er sant at:
(4 R) ^ 2 = a ^ 2 + a ^ 2 = 2 a ^ 2
Derfor er forholdet kant-radius:
a / R = 4 / √2
Øvelse 2
Finn forholdet mellom gitterparameteren og atomradiusen for et kubisk gitter I (kroppssentrert).
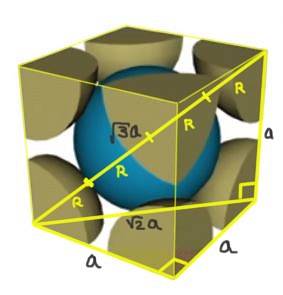
Løsning: Atomer antas å være representert som kuler hele radius R i "kontakt" med hverandre, som vist på figuren.
To rette trekanter dannes, den ene av hypotenuse √2a og den andre av hypotenuse √3a som det kan bevises ved bruk av Pythagoras teorem. Derfra følger det at forholdet mellom gitterparameteren og atomradiusen for et kubisk gitter I (sentrert i kroppen) er:
a / R = 4 / √3
Øvelse 3
Finn pakkingsfaktoren F for en enhetscelle med en kubikkstruktur F (ansiktssentrert kubikk) der atomene har radius R og er i "kontakt".
Løsning: Pakningsfaktoren F er definert som kvotienten mellom volumet okkupert av atomene i enhetscellen og volumet til cellen:
F = Vatomer / Vcelle
Som demonstrert ovenfor er antall atomer per celleenhet i et ansiktssentrert kubisk gitter 4, så pakningsfaktoren vil være:
F = 4 [4πR ^ 3/3] / [a ^ 3] =…
… 4 [4πR ^ 3/3] / [4R / √2] ^ 3 = (√2) π / 6 = 0,74
Referanser
- Crystal Structures Academic Resource Center. [PDF]. Hentet 24. mai 2018 fra: web.iit.edu
- Krystaller. Hentet 26. mai 2018 fra: thoughtco.com
- Pressebøker. 10.6 Gitterstrukturer i krystallinske faste stoffer. Hentet 26. mai 2018 fra: opentextbc.ca
- Ming. (2015, 30. juni). Typer krystallstrukturer. Hentet 26. mai 2018 fra: crystalvisions-film.com
- Helmenstine, Anne Marie, Ph.D. (31. januar 2018). Typer av
- Kittel Charles (2013) Solid State Physics, Condensed matter Physics (8. utgave). Wiley.
- KHI. (2007). Krystallinske strukturer. Hentet 26. mai 2018, fra: folk.ntnu.no
- Wikipedia. Bravais gitter. Gjenopprettet fra: en.wikipedia.com.



Ingen har kommentert denne artikkelen ennå.