De økuasjonssystemer De består av to eller flere ligninger med flere variabler som må ha en felles løsning. De er hyppige, fordi det i praksis er mange situasjoner som avhenger av mange faktorer, som er relatert på forskjellige måter.
Generelt har et ligningssystem følgende form, der hver funksjon representerer en av betingelsene som løsningen må tilfredsstille:
La oss se et eksempel: anta at du trenger å lage rektangulære ark med et område på 180 cmto og som har en omkrets på 54 cm. Hva skal være dimensjonene på arket?
For å svare på spørsmålet tar vi hensyn til at dimensjonene til et rektangulært ark er to: bredde og høyde. Dette betyr at vi har to variabler som vi vil gi de vanlige navnene på x og Y.
Og disse variablene må tilfredsstille de to betingelsene som er pålagt samtidig:
-Første tilstand: arket er 180 cmto. Dette vil være den første funksjonen: F1.
-Andre tilstand: arkets omkrets eller kontur må være 54 cm. Dette er den andre funksjonen Fto.
For hver tilstand etableres en ligning ved bruk av algebraisk språk. Området A på et rektangulært ark oppnås ved å multiplisere bredden med høyden:
A = x.y = 180 cmto
Og omkretsen P er resultatet av å legge til sidene. Siden omkretsen er summen av sidene:
P = 2x + 2y = 54 cm
Det resulterende systemet med to ligninger og to ukjente er:
xy = 180
2 (x + y) = 54
Vi trenger to tall hvis produkt er 180 og det doble produktet av summen er 54, eller hva er det samme: tilsammen må de gi 27. Disse tallene er 12 og 15.
I delen av løste øvelser vil vi tilby den detaljerte metoden for å finne disse verdiene, i mellomtiden kan leseren enkelt verifisere ved å erstatte at de effektivt tilfredsstiller begge ligningene.
Artikkelindeks
Situasjonen som er foreslått ovenfor inneholder to variabler, og det kreves minst to ligninger for å finne dem. Det er systemer med mange flere variabler, men i alle fall, hvis systemet har det n av dem krever det i det minste n ligninger uavhengig av hverandre (man kan ikke være en lineær kombinasjon av de andre) for å finne løsningen, hvis den eksisterer.
Når det gjelder applikasjonene, er de mange. Her er noen hvor ligningssystemer viser at de er nyttige:
-Finne strømmen som strømmer gjennom en krets ved å bruke Kirchoffs lover.
-I land- og lufttransport for å etablere avgangs- og ankomsttider.
-Finn størrelsen på krefter i dynamiske eller statiske systemer som er gjenstand for flere interaksjoner.
-Å vite hvor mange varer som er solgt i løpet av en viss tidsperiode, eller i fabrikker, for å bestemme dimensjonene på gjenstander slik at de oppfyller visse betingelser når det gjelder overflate eller volum.
-Når du bestemmer hvordan du skal fordele en kapital i forskjellige investeringer.
-Sett prisene for ulike tjenester, for eksempel telekommunikasjon eller show, og vis hvor mye penger som samles inn (se løst eksempel 2)
-En ligning er valgt og en av variablene er løst.
-Da må vi erstatte den fjernede variabelen i en annen ligning. Da forsvinner denne variabelen derfra, og hvis systemet har to ligninger og to ukjente, forblir det en ligning med en variabel som allerede kan løses.
-Hvis systemet har mer enn to variabler, må vi løse en tredje ukjent fra en annen ligning og erstatte den også.
Et eksempel på anvendelse av denne metoden er i løst oppgave 1.
Denne metoden består i å legge til eller trekke ligninger for å eliminere en eller flere variabler og bare la være en. For å gjøre dette er det praktisk å multiplisere ligningene med en faktor slik at når det legges sammen med en annen ligning, forsvinner det ukjente. La oss se et eksempel:
3xto - Yto = 11
xto + 4yto = 8
Vi multipliserer den første ligningen med 4:
12xto - 4yto = 44
xto + 4yto = 8
Ved å legge dem til forsvinner det ukjente Y, gjenstående:
13xto = 52
xto = 4
Derfor x1 = 2 og xto = -2. Med disse verdiene kan leseren sjekke det og1 = 1 og yto = -1
Når systemet er to ligninger med to ukjente:
-Velg et ukjent og løs for begge ligningene.
-Resultatene utjevnes, noe som gjør det mulig å oppnå en enkelt ligning med en enkelt ukjent.
-Denne ligningen er løst og resultatet erstattes i en av de foregående klareringene for å oppnå verdien av den andre ukjente..
Denne metoden vil bli brukt i løst oppgave 2 i det følgende avsnitt.
Denne metoden består i å tegne kurver som hver ligning representerer. Skjæringspunktet er løsningen på systemet. Følgende eksempel viser den grafiske løsningen til systemet:
xto + Y to = 1
2x + 4y = 0
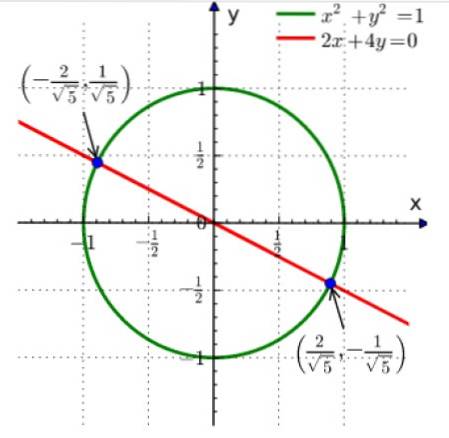
Den første av ligningene er en sirkel med radius 1 sentrert ved opprinnelsen, og den andre er en linje.
Krysset mellom begge er de to punktene vist i blått. Leseren kan verifisere at ved å erstatte koordinatene til punktene i ovenstående ligninger, oppnås en likhet.
Du må lage rektangulære papirark med et område på 180 cmto og med en omkrets på 54 cm. Hva skal være dimensjonene på arket?
Systemet som skal løses er:
xy = 180
2 (x + y) = 54
Den andre ligningen kan forenkles til x + y = 27, derfor:
xy = 180
x + y = 27
Løs for en av de ukjente i den andre ligningen:
y = 27 - x
Klarering erstattes i den første:
(27 -x) = 180
Bruk av distribusjonseiendom:
-xto + 27x = 180
Multipliser med (-1) på begge sider av ligningen og send 180 til venstre:
xto - 27x +180 = 0
Resultatet er en ligning av andre grad i x, som løses med formelen:
Med a = 1, b = -27 og c = 180
En fornøyelsespark har følgende inngangsgebyrer: barn $ 1,5 og voksne $ 4. På en dag var det 2200 besøkende, og samlet $ 5050. Finn antall barn og voksne som besøkte parken den dagen.
Være x antall barn og Y antall voksne. Vi kan etablere den første av ligningene og vite at summen av begge må være 2200:
x + y = 2200.
Nå går vi med de innsamlede pengene. Prisen på barnebilletten er $ 1,5 for hvert barn, ved å multiplisere denne verdien med x, antall barn, vil vi ha beløpet for barnebilletten:
1,5x = penger samlet inn for barnebilletter
Og hvis vi multipliserer $ 4 per voksen med antall og antall voksne besøkende, får vi de totale pengene for alle voksne:
4y = penger samlet inn av billetter til voksne
Vi legger dette sammen for å få $ 5050:
1,5x + 4y = 5050
Vårt ligningssystem er:
x + y = 2200
1,5x + 4y = 5050
La oss løse det ved utjevning. Vi isolerer variabelen y fra den første og den andre ligningen:
y = 2200 - x
y = (5050 - 1,5 x) / 4
Vi samsvarer med begge uttrykkene:
2200 - x = (5050 - 1,5x) / 4
Vi multipliserer alt med 4 for å eliminere brøkdelen:
8800 - 4x = 5050 - 1,5x
Vi grupperer ordene med x til venstre og de rene tallene til høyre:
-4x + 1,5x = 5050 - 8800
-2,5x = -3750
x = 1500 barn.
Vi erstatter denne verdien i y = 2200 - x for å finne antall voksne:
y = 2200 - 1500 = 700 voksne.
Ingen har kommentert denne artikkelen ennå.