
Bolzanos teorem Forklaring, applikasjoner og øvelser
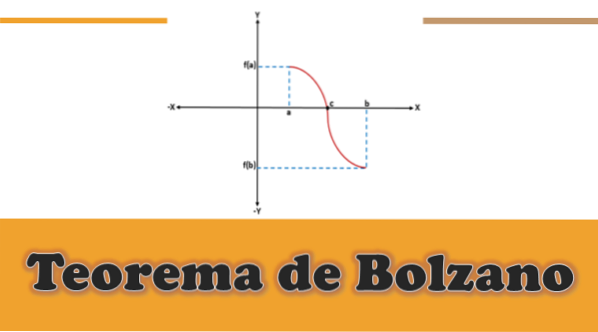
De Bolzanos teorem fastslår at hvis en funksjon er kontinuerlig på alle punkter i et lukket intervall [a, b] og det er sant at bildet av "a" og "b" (under funksjonen) har motsatte tegn, så vil det være minst ett punkt "C" i det åpne intervallet (a, b), på en slik måte at funksjonen evaluert i "c" vil være lik 0.
Denne teoremet ble bekjentgjort av filosofen, teologen og matematikeren Bernard Bolzano i 1850. Denne forskeren, født i dagens Tsjekkia, var en av de første matematikerne i historien som gjorde et formelt bevis på egenskapene til kontinuerlige funksjoner..
Artikkelindeks
- 1 Forklaring
- 2 Demo
- 3 Hva er det til??
- 4 Løst øvelser
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 5 Referanser
Forklaring
Bolzanos teorem er også kjent som mellomverdisetningen, som hjelper til med å bestemme bestemte verdier, spesielt nuller, for visse reelle funksjoner til en reell variabel.
I en gitt funksjon fortsetter f (x) - det vil si at f (a) og f (b) er forbundet med en kurve-, hvor f (a) er under x-aksen (den er negativ), og f ( b) ved over x-aksen (den er positiv), eller omvendt, vil det grafisk være et avskjæringspunkt på x-aksen som vil representere en mellomverdi "c", som vil være mellom "a" og “B”, og verdien av f (c) vil være lik 0.
Ved grafisk å analysere Bolzanos teorem, kan det sees at for hver kontinuerlig funksjon f definert i et intervall [a, b], hvor f (a)*f (b) er mindre enn 0, vil det være minst en rot "c" for den funksjonen innenfor intervallet (a, b).
Denne setningen fastslår ikke antall punkter i det åpne intervallet, den sier bare at det er minst 1 poeng.
Demonstrasjon
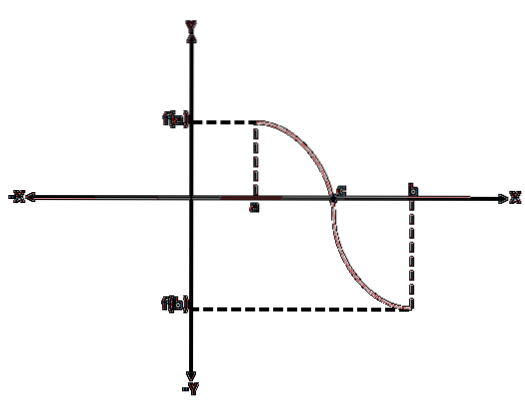
For å bevise Bolzanos teorem antas det uten tap av generalitet at f (a) < 0 y f(b) > 0; dermed kan det være mange verdier mellom "a" og "b" hvor f (x) = 0, men det er bare nødvendig å vise at det er en.
Vi begynner med å evaluere f i midtpunktet (a + b) / 2. Hvis f ((a + b) / 2) = 0, slutter beviset her; ellers er f ((a + b) / 2) positiv eller negativ.
En av halvdelene av intervallet [a, b] er valgt, slik at tegnene på funksjonen som er evaluert i ytterpunktene, er forskjellige. Dette nye intervallet vil være [a1, b1].
Nå, hvis f evaluert ved midtpunktet til [a1, b1] ikke er null, blir den samme operasjonen som før utført; det vil si at halvparten av dette intervallet er valgt som oppfyller betingelsen for skiltene. La dette nye intervallet være [a2, b2].
Hvis du fortsetter med denne prosessen, vil du ha to sekvenser an og bn, slik at:
an øker og bn avtar:
a ≤ a1 ≤ a2 ≤… ≤ an ≤…. ≤…. ≤ bn ≤…. ≤ b2 ≤ b1 ≤ b.
Hvis lengden på hvert intervall [ai, bi] beregnes, vil vi ha:
b1-a1 = (b-a) / 2.
b2-a2 = (b-a) / 2².
... .
bn-an = (b-a) / 2 ^ n.
Derfor er grensen som n tendens til uendelig av (bn-an) lik 0.
Ved å bruke at an øker og avgrenses og bn avtar og avgrenses, har vi at det eksisterer en verdi "c" slik at:
a ≤ a1 ≤ a2 ≤… ≤ an ≤… .≤ c ≤…. ≤ bn ≤…. ≤ b2 ≤ b1 ≤ b.
Grensen for en er "c" og grensen for bn er også "c". Gitt et hvilket som helst δ> 0, er det alltid et "n" slik at intervallet [an, bn] er inneholdt i intervallet (c-δ, c + δ).
Nå må det vises at f (c) = 0.
Hvis f (c)> 0, da f er kontinuerlig, eksisterer det en ε> 0 slik at f er positiv over hele intervallet (c-ε, c + ε). Som nevnt ovenfor er det imidlertid en verdi "n" slik at f endrer tegn i [an, bn], og dessuten er [an, bn] inneholdt i (c-ε, c + ε), hvilket motsigelse.
Hvis f (c) < 0, entonces como f es continua, existe un ε >0 slik at f er negativ gjennom hele intervallet (c-ε, c + ε); men det er en verdi "n" slik at f endrer tegn i [an, bn]. Det viser seg at [an, bn] er inneholdt i (c-ε, c + ε), som også er en motsetning.
Derfor er f (c) = 0, og dette er hva vi ønsket å vise.
Hva er den til?
Fra sin grafiske tolkning brukes Bolzanos teorem for å finne røtter eller nuller i en kontinuerlig funksjon, gjennom halvering (tilnærming), som er en inkrementell søkemetode som alltid deler intervallene med 2.
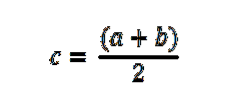
Deretter tas et intervall [a, c] eller [c, b] der tegnendringen skjer, og prosessen gjentas til intervallet er mindre og mindre, for å komme nærmere ønsket verdi; det vil si til verdien som funksjonen gjør 0.
Oppsummert, for å anvende Bolzanos teorem og dermed finne røttene, begrense nullene til en funksjon eller gi en løsning på en ligning, utføres følgende trinn:
- Det bekreftes om f er en kontinuerlig funksjon i intervallet [a, b].
- Hvis intervallet ikke er gitt, må man finne der funksjonen er kontinuerlig.
- Det verifiseres hvis ytterpunktene i intervallet gir motsatte tegn når de blir evaluert ved f.
- Hvis ingen motsatte tegn oppnås, må intervallet deles i to underintervaller ved hjelp av midtpunktet.
- Evaluer funksjonen ved midtpunktet og verifiser at Bolzano-hypotesen er oppfylt, der f (a) * f (b) < 0.
- Avhengig av tegnet (positivt eller negativt) på verdien som blir funnet, gjentas prosessen med et nytt delintervall til den nevnte hypotesen er oppfylt..
Løst øvelser
Øvelse 1
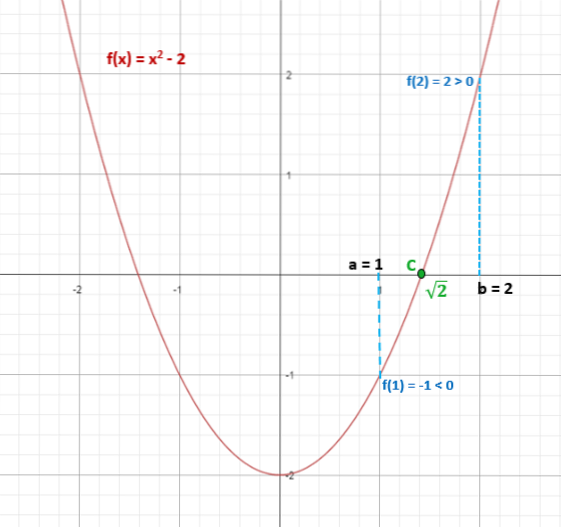
Bestem om funksjonen f (x) = xto - 2, har minst en reell løsning i intervallet [1,2].
Løsning
Vi har funksjonen f (x) = xto - 2. Siden det er polynom, betyr det at det er kontinuerlig i alle intervaller.
Det blir bedt om å avgjøre om den har en reell løsning i intervallet [1, 2], så nå er det bare nødvendig å erstatte ytterpunktene til intervallet i funksjonen for å kjenne tegnet på disse og å vite om de oppfyller vilkåret av å være annerledes:
f (x) = xto - to
f (1) = 1to - 2 = -1 (negativ)
f (2) = 2to - 2 = 2 (positivt)
Derfor tegn på f (1) ≠ tegn f (2).
Dette sikrer at det er minst ett punkt "c" som hører til intervallet [1,2], der f (c) = 0.
I dette tilfellet kan verdien av "c" enkelt beregnes som følger:
xto - 2 = 0
x = ± √2.
Dermed tilhører √2 ≈ 1,4 intervallet [1,2] og oppfyller at f (√2) = 0.
Øvelse 2
Vis at ligningen x5 + x + 1 = 0 har minst en reell løsning.
Løsning
La oss først legge merke til at f (x) = x5 + x + 1 er en polynomfunksjon, som betyr at den er kontinuerlig på alle reelle tall.
I dette tilfellet er det ikke gitt noe intervall, så verdiene må velges intuitivt, helst nær 0, for å evaluere funksjonen og finne tegnendringene:
Hvis du bruker intervallet [0, 1], må du:
f (x) = x5 + x + 1.
f (0) = 05 + 0 + 1 = 1> 0.
f (1) = 15 + 1 + 1 = 3> 0.
Siden det ikke er noen tegnendring, gjentas prosessen med et annet intervall.
Hvis du bruker intervallet [-1, 0], må du:
f (x) = x5 + x + 1.
f (-1) = (-1)5 + (-1) + 1 = -1 < 0.
f (0) = 05 + 0 + 1 = 1> 0.
I dette intervallet er det en tegnendring: tegn på f (-1) ≠ tegn på f (0), som betyr at funksjonen f (x) = x5 + x + 1 har minst en ekte rot “c” i intervallet [-1, 0], slik at f (c) = 0. Med andre ord er det sant at x5 + x + 1 = 0 har en reell løsning i intervallet [-1,0].
Referanser
- Bronshtein I, S. K. (1988). Matematikkhåndbok for ingeniører og studenter ... Redaksjonell MIR.
- George, A. (1994). Matematikk og sinn. Oxford University Press.
- Ilín V, P. E. (1991). Matematisk analyse. I tre bind ...
- Jesús Gómez, F. G. (2003). Videregående lærere. Volum II. GAL.
- Mateos, M. L. (2013). Grunnleggende egenskaper for analyse i R. Editores, 20. des.
- Piskunov, N. (1980). Differensiell og integrert kalkulator ...
- Sydsaeter K, H. P. (2005). Matematikk for økonomisk analyse. Felix Varela.
- William H. Barker, R. H. (s.f.). Kontinuerlig symmetri: Fra Euclid til Klein. American Mathematical Soc.



Ingen har kommentert denne artikkelen ennå.