
Chebyshovs teorem hva det er, applikasjoner og eksempler
De Chebyshovs teorem (eller Chebyshovs ulikhet) er en av de viktigste klassiske resultatene av sannsynlighetsteori. Det tillater estimering av sannsynligheten for en hendelse beskrevet i form av en tilfeldig variabel X, ved å gi oss en avgrensning som ikke avhenger av fordelingen av den tilfeldige variabelen, men av variansen av X.
Teoremet er oppkalt etter den russiske matematikeren Pafnuty Chebyshov (også skrevet som Chebychev eller Tchebycheff) som, til tross for at han ikke var den første som uttalte setningen, var den første som ga et bevis i 1867.

Denne ulikheten, eller de som på grunn av deres egenskaper kalles Chebyshovs ulikhet, brukes hovedsakelig til å tilnærme sannsynligheter ved å beregne grenser.
Artikkelindeks
- 1 Hva gjør?
- 2 Applikasjoner og eksempler
- 2.1 Begrensning av sannsynligheter
- 2.2 Bevis på grensesetninger
- 2.3 Prøvestørrelse
- 3 ulikheter av typen Chebyshov
- 4 Referanser
Hva består den av?
I studien av sannsynlighetsteori hender det at hvis fordelingsfunksjonen til en tilfeldig variabel X er kjent, kan dens forventede verdi -eller matematisk forventning E (X) - og dens varians Var (X) beregnes så lenge slike mengder eksisterer . Imidlertid er det omvendte ikke nødvendigvis sant..
Det vil si at det å kjenne E (X) og Var (X) ikke nødvendigvis er mulig å oppnå fordelingsfunksjonen til X, og derfor er størrelser som P (| X |> k) for noen k> 0 veldig vanskelige å oppnå. Men takket være Chebyshovs ulikhet er det mulig å estimere sannsynligheten for den tilfeldige variabelen.
Chebyshovs teorem forteller oss at hvis vi har en tilfeldig variabel X over et prøverom S med en sannsynlighetsfunksjon p, og hvis k> 0, så:
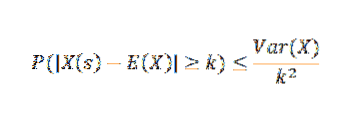
Søknader og eksempler
Blant de mange anvendelsene av Chebyshovs teorem kan følgende nevnes:
Begrensende sannsynlighet
Dette er den vanligste applikasjonen og brukes til å gi en øvre grense for P (| X-E (X) | ≥k) hvor k> 0, bare med variansen og forventningen til den tilfeldige variabelen X, uten å vite sannsynlighetsfunksjonen.
Eksempel 1
Anta at antall produkter produsert i et selskap i løpet av en uke er en tilfeldig variabel med et gjennomsnitt på 50.
Hvis det er kjent at variansen til en produksjonsuke er lik 25, hva kan vi si om sannsynligheten for at denne uken er produksjonen forskjellig med mer enn 10 fra gjennomsnittet?
Løsning
Ved å bruke Chebyshovs ulikhet har vi:
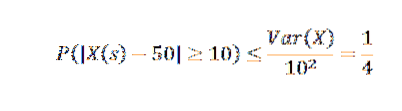
Fra dette kan vi oppnå at sannsynligheten for at antall artikler i produksjonsuken overstiger gjennomsnittet med mer enn 10 er maksimalt 1/4.
Bevis på grensesetninger
Chebyshovs ulikhet spiller en viktig rolle i å bevise de viktigste grensesetningene. Som et eksempel har vi følgende:
Svak lov av stort antall
Denne loven fastslår at gitt en sekvens X1, X2,…, Xn, ... av uavhengige tilfeldige variabler med samme gjennomsnittsfordeling E (Xi) = μ og varians Var (X) = σto, og et kjent middelprøve av:
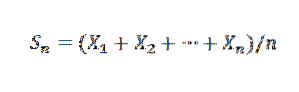
Så for k> 0 har vi:
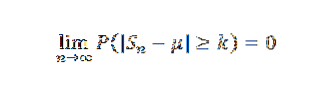
Eller tilsvarende:
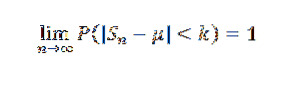
Demonstrasjon
La oss først legge merke til følgende:
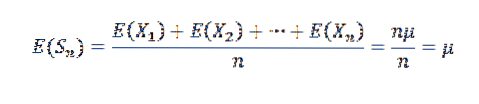
Siden X1, X2, ..., Xn er uavhengige, følger det at:
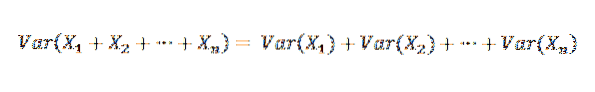
Derfor er det mulig å si følgende:
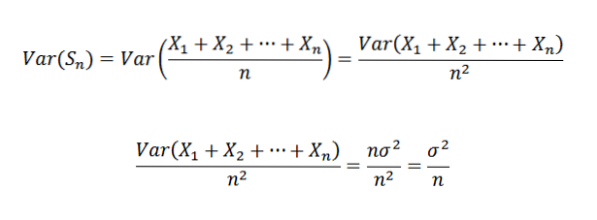
Deretter bruker vi Chebyshovs teorem:
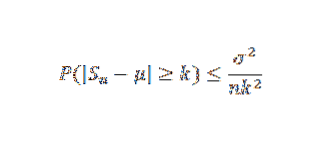
Til slutt kommer teoremet fra det faktum at grensen til høyre er null når n har en tendens til uendelig.
Det skal bemerkes at denne testen bare ble gjort for tilfellet der avviket til Xi eksisterer; det vil si at den ikke avviker. Dermed observerer vi at teoremet alltid er sant hvis E (Xi) eksisterer.
Chebyshov begrense teorem
Hvis X1, X2,…, Xn,… er en sekvens av uavhengige tilfeldige variabler slik at det er noe C< infinito, tal que Var(Xn) ≤ C para todo n natural, entonces para cualquier k>0:
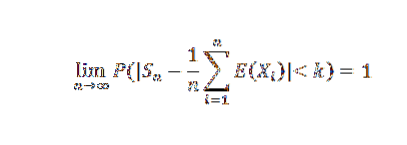
Demonstrasjon
Siden avvikssekvensen er jevnt avgrenset, har vi den Var (Sn) ≤ C / n, for alle naturlige n. Men vi vet at:
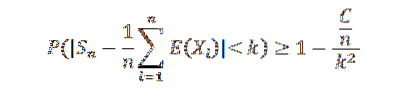
Gjør n tendens til uendelig, følgende resultater:
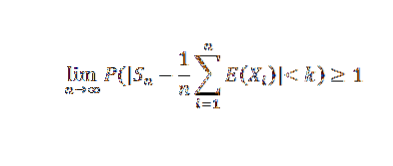
Siden en sannsynlighet ikke kan overstige verdien 1, oppnås ønsket resultat. Som en konsekvens av denne teoremet kunne vi nevne den spesielle saken om Bernoulli.
Hvis et eksperiment gjentas n ganger uavhengig med to mulige utfall (fiasko og suksess), hvor p er sannsynligheten for suksess i hvert eksperiment og X er den tilfeldige variabelen som representerer antall oppnådde suksesser, så for hver k> 0 du har til:
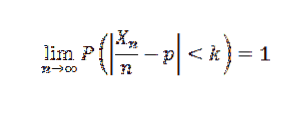
Prøvestørrelse
Når det gjelder variansen, tillater Chebyshov-ulikheten oss å finne en utvalgstørrelse n som er tilstrekkelig til å garantere at sannsynligheten for at | Sn-μ |> = k oppstår er så liten som ønsket, noe som gjør at vi kan ha en tilnærming til gjennomsnitt.
La X1, X2, ... Xn være et utvalg av uavhengige tilfeldige variabler av størrelse n og anta at E (Xi) = μ og dens varians σto. Så av Chebyshovs ulikhet har vi:
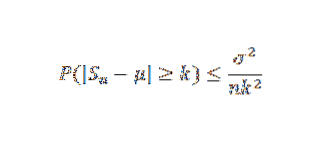
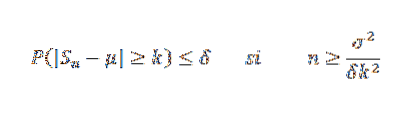
Eksempel
Anta at X1, X2, ... Xn er et utvalg av uavhengige tilfeldige variabler med Bernoulli-fordeling, slik at de tar verdien 1 med sannsynlighet p = 0,5.
Hva skal være størrelsen på prøven for å kunne garantere at sannsynligheten for at forskjellen mellom aritmetisk gjennomsnitt Sn og dens forventede verdi (overstiger mer enn 0,1), er mindre enn eller lik 0., 01?
Løsning
Vi har at E (X) = μ = p = 0,5 og at Var (X) = σto= p (1-p) = 0,25. Ved Chebyshovs ulikhet har vi for alle k> 0:
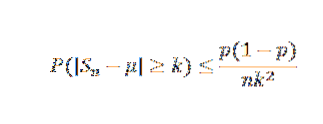
Nå tar vi k = 0,1 og δ = 0,01, og vi har:
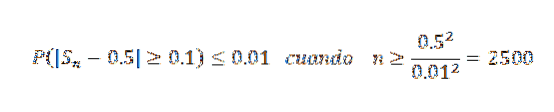
På denne måten konkluderes det med at det er behov for en prøvestørrelse på minst 2500 for å garantere at sannsynligheten for hendelsen | Sn - 0,5 |> = 0,1 er mindre enn 0,01.
Ulikheter av typen Chebyshov
Det er flere ulikheter knyttet til Chebyshovs ulikhet. En av de mest kjente er Markov-ulikhetene:
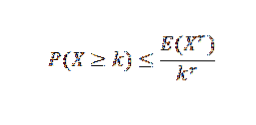
I dette uttrykket er X en ikke-negativ tilfeldig variabel med k, r> 0.
Markov-ulikheten kan ta forskjellige former. La for eksempel Y være en ikke-negativ tilfeldig variabel (så P (Y> = 0) = 1) og anta at E (Y) = μ eksisterer. Anta også at (E (Y))r= μr eksisterer for noe heltall r> 1. Deretter:
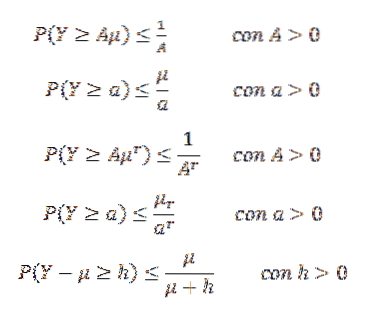
En annen ulikhet er Gaussian, som forteller oss at gitt en unimodal tilfeldig variabel X med modus på null, så for k> 0,
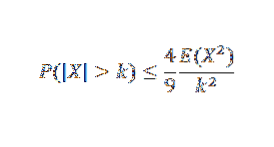
Referanser
- Kai Lai Chung. Elementær sannsynlighetsteori med stokastiske prosesser. Springer-Verlag New York Inc.
- Kenneth.H. Rosen. Diskret matematikk og dens applikasjoner. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Sannsynlighet og statistiske applikasjoner. S.A. MEKSIKANSK ALHAMBRA.
- Seymour Lipschutz Ph.D. 2000 Løste problemer med diskret matematikk. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Teori og sannsynlighetsproblemer. McGRAW-HILL.



Ingen har kommentert denne artikkelen ennå.