Varignons setning

Hva er Varignons teorem?

Varignons teorem, i Mechanics, sier at summen av momentene produsert av et system av samtidige krefter i forhold til et bestemt punkt er lik øyeblikket til den resulterende kraften med hensyn til samme punkt.

Av denne grunn er denne teoremet også kjent som begynnelsen på øyeblikkene.

Selv om den første som fortalte det var nederlenderen Simon Stevin (1548-1620), skaperen av det hydrostatiske paradokset, var den franske matematikeren Pierre Varignon (1654-1722) den som senere ga den sin endelige form.

Et eksempel på hvordan Varignons teorem fungerer i mekanikk er følgende: antar at et enkelt system med to koplanære og samtidige krefter virker på et punkt F₁ Y F_to, (betegnet med fet skrift på grunn av vektortegnet). Disse kreftene gir opphav til en netto eller resulterende kraft, kalt F_R.

Hver kraft utøver et dreiemoment eller moment rundt et punkt O, som beregnes av vektorproduktet mellom posisjonsvektoren r_OP og styrken F, hvor r_OP er dirigert fra O til punktet med samtidighet P:

M_O1 = r_OP × F₁

M_O2 = r_OP × F_to

Gitt F_R = F₁ + F_to, deretter:

M_ELLER = r_OP × F₁ + r_OP × F_to = M_O1 + M_O2

Men hvordan r_OP er en vanlig faktor, da anvendelse av distribuerende eiendom på kryssproduktet:

M_ELLER = r_OP × (F₁ + F_to) = r_OP × F_R                

Derfor er summen av momentene eller momentene til hver kraft i forhold til punkt O ekvivalent med øyeblikket til den resulterende kraften i forhold til det samme punktet.

Erklæring og bevis

La være et system av N samtidige krefter, dannet av F₁, F_to, F₃... F_N, hvis handlingslinjer krysser seg ved punkt P (se figur 1), øyeblikket til dette styrkesystemet M_ELLER, med hensyn til et punkt O er gitt av:

M_ELLER = r_OP × F₁ + r_OP × F_to + r_OP × F₃ +... r_OP × F_N = r_OP × (F₁ + F_to + F₃ +... F_N)

Demonstrasjon

For å bevise teoremet brukes den distribuerende egenskapen til vektorproduktet mellom vektorene.

Vær kreftene F₁, F_to, F₃... F_N brukt på punkt A₁, TIL_to, TIL₃… TIL_N og samtidig ved punkt P. Det resulterende øyeblikket til dette systemet, med hensyn til et punkt O, kalt M_ELLER, er summen av øyeblikkene til hver styrke, med hensyn til nevnte punkt:

M_ELLER = ∑ r_OAi × F_Jeg

Der summen går fra i = 1 til i = N, siden det er N-krefter. Når vi har å gjøre med samtidige krefter, og siden vektorproduktet mellom parallelle vektorer er null, skjer det at:

r_PAi × F_Jeg = 0

Med nullvektoren betegnet som 0.

Øyeblikket til en av kreftene i forhold til O, for eksempel kraftens F_Jeg anvendt i A_Jeg, det er skrevet slik:

M_{jeg hørte} = r_OAi × F_Jeg

Posisjonsvektoren r_OAi  kan uttrykkes som summen av to posisjonsvektorer:

r_OAi = r_OP + r_PAi

På denne måten, øyeblikket om O av styrken F_Jeg Det er:

M_{jeg hørte} = (r_OP + r_PAi) × F_Jeg = (r_OP × F_Jeg) + (r_PAi × F_Jeg)

Men det siste begrepet er null, som forklart ovenfor, fordi r_PAi er på handlingslinjen til F_Jeg, Og dermed:

M_{jeg hørte} = r_OP × F_Jeg

Å vite at øyeblikket til systemet med hensyn til punkt O er summen av alle individuelle øyeblikk for hver kraft i forhold til nevnte punkt, så:

M_ELLER = ∑ M_{jeg hørte} = ∑ r_OP × F_Jeg

Hva r_OP er konstant kommer ut av summen:

M_ELLER = r_OP × (∑ F_Jeg)

Men ∑ F_Jeg er rett og slett nettokraften eller den resulterende kraften F_R, derfor konkluderes det umiddelbart at:

M_ELLER = r_OP × F_R

Eksempel

Varignons setning letter beregningen av kraftmomentet F Med hensyn til punkt O i strukturen vist på figuren, hvis kraften spaltes i dets rektangulære komponenter og øyeblikket til hver av dem beregnes:

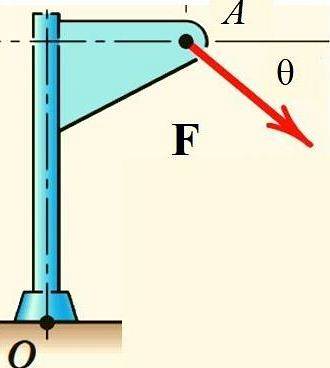
Anvendelser av Varignons teorem

Når den resulterende kraften til et system er kjent, kan Varignons setning brukes for å erstatte summen av hvert av øyeblikkene som produseres av kreftene som komponerer det med øyeblikket til den resulterende.

Hvis systemet består av krefter på samme plan og punktet som øyeblikket skal beregnes til tilhører det planet, er det resulterende øyeblikket vinkelrett.

For eksempel, hvis alle kreftene er i xy-planet, blir øyeblikket rettet i z-aksen, og det gjenstår bare å finne sin størrelse og sin forstand, slik er eksemplet beskrevet ovenfor.

I dette tilfellet lar Varignons teorem oss beregne det resulterende øyeblikket til systemet gjennom summeringen. Det er veldig nyttig når det gjelder et tredimensjonalt kraftsystem der retningen av det resulterende øyeblikket ikke er kjent på forhånd.

For å løse disse øvelsene er det praktisk å nedbryte krefter og posisjonsvektorer i deres rektangulære komponenter, og fra summen av øyeblikkene bestemme komponentene i nettomomentet.

Treningen løst

Bruk Varignons teorem til å beregne momentet for kraften F rundt punktet O vist i figuren hvis størrelsen på F er 725 N.

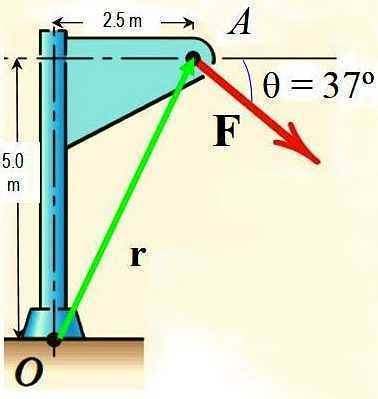
Løsning

For å anvende Varignons teorem, spalt styrken F i to komponenter, hvis respektive øyeblikk rundt O beregnes og legges til for å oppnå det resulterende øyeblikket.

F_x = 725 N ∙ cos 37 º = 579,0 N

F_Y = - 725 N N ∙ sin 37 º = −436,3 N

Tilsvarende posisjonsvektoren r rettet fra O til A har komponentene:

r_x = 2,5 m

r_Y = 5,0 m

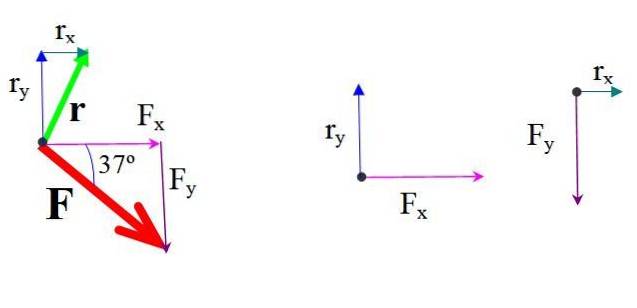
Momentet til hver komponent av kraften rundt O blir funnet ved å multiplisere kraften og den vinkelrette avstanden.

Begge kreftene har en tendens til å rotere strukturen i samme retning, som i dette tilfellet er med klokken, som et positivt tegn vilkårlig er tildelt:

M_Okse = F_x∙ r_Y ∙ sin 90º = 579,0 N ∙ 5,0 m = 2895 N ∙ m

M_Oy = F_Y∙ r_x ∙ sin (−90º) = −436,3 N ∙ 2,5 m ∙ (−1) = 1090,8 N ∙ m

Det resulterende øyeblikket om O er:

M_ELLER = M_Okse + M_Oy = 3985,8 N ∙ m vinkelrett på planet og med klokken.

Referanser

1. Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 
2. Beer, F. 2010. Statisk. McGraw Hill. 9. plass. Utgave.
3. Hibbeler, R. 1992. Mekanikk for ingeniører. Sjette. Utgave. CECSA.
4. HK Engineering. Varignons setning. Gjenopprettet fra: youtube.com.
5. Wikipedia. Varignons teorem (Mekanikk). Gjenopprettet fra: en.wikipedia.org.