
Mekanisk arbeid hva er det, forhold, eksempler, øvelser
De mekanisk arbeid Det er definert som endringen i energisituasjonen til et system, forårsaket av virkningen av eksterne krefter som tyngdekraft eller friksjon. Enhetene for mekanisk arbeid i International System (SI) er newton x meter eller joule, forkortet med J.
Matematisk er det definert som skalarproduktet til kraftvektoren og forskyvningsvektoren. Ja F er den konstante kraften og l er forskyvningen, begge vektorer, blir arbeidet W uttrykt som: W = F ● l

Når kraften ikke er konstant, må vi analysere arbeidet som er utført når forskyvningene er veldig små eller differensielle. I dette tilfellet, hvis punkt A betraktes som startpunktet og B som ankomstpunktet, oppnås det totale arbeidet ved å legge til alle bidragene til det. Dette tilsvarer beregning av følgende integral:
Variasjon i systemets energi = Arbeid utført av eksterne krefter
ΔE = Wekst
Når energi tilsettes systemet, W> 0 og når energi trekkes fra W<0. Ahora bien, si ΔE = 0, puede significar que:
-Systemet er isolert og det er ingen eksterne krefter som virker på det.
-Det er eksterne krefter, men de jobber ikke med systemet.
Siden endringen i energi tilsvarer arbeidet som utføres av eksterne krefter, er SI-enheten for energi også joule. Dette inkluderer alle typer energi: kinetisk, potensiell, termisk, kjemisk og mer..
Artikkelindeks
- 1 Vilkår for mekanisk arbeid å eksistere
- 1.1 Tegn på arbeid
- 2 Eksempler på mekanisk arbeid
- 3 Arbeidskinetisk energisetning
- 3.1 Arbeidet er gjort for å strekke en fjær
- 4 Øvelser
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 5 Referanser
Forhold for at det skal være mekanisk arbeid
Vi har allerede sett at arbeid er definert som et punktprodukt. La oss ta definisjonen av arbeid utført med en konstant kraft og bruke konseptet med prikkproduktet mellom to vektorer:
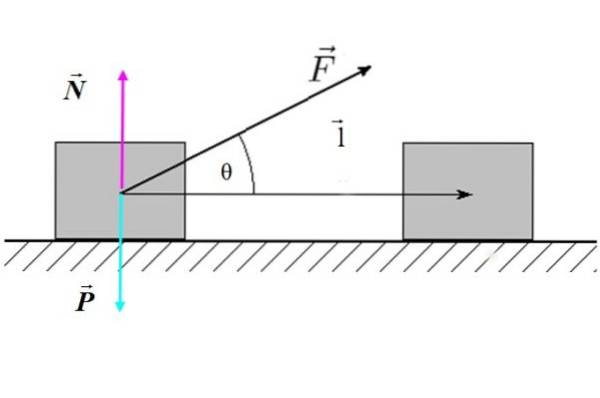
W = F ● l = F.l.cos θ
Hvor F er styrkeens styrke, l er størrelsen på forskyvningen og θ er vinkelen mellom kraften og forskyvningen. I figur 2 er det et eksempel på en skrå ekstern kraft som virker på en blokk (systemet), som produserer en horisontal forskyvning.

Omskrive arbeidet som følger:
W = (F. cos θ). l
Vi kan si at bare komponenten av kraften som er parallell med forskyvningen: F. cos θ eer i stand til å gjøre arbeid. Hvis θ = 90 º, vil cos θ = 0 og verket være null.
Derfor konkluderes det med at kreftene vinkelrett på forskyvningen ikke utfører mekanisk arbeid.
I tilfelle av figur 2, verken den normale kraften N ei heller vekten P gjør arbeid, siden begge er vinkelrett på forskyvningen l.
Tegn på arbeid
Som forklart ovenfor, W Det kan være positivt eller negativt. Når cos θ> 0, arbeidet utført av kraften er positivt, siden det har samme bevegelsesretning.
Ja cos θ = 1, kraft og forskyvning er parallelle og arbeid er maksimalt.
I tilfelle cos θ < 1, la fuerza no está a favor del movimiento y el trabajo es negativo.
Når cos θ = -1, kraft er helt motsatt forskyvning, for eksempel kinetisk friksjon, hvis effekt er å bremse gjenstanden som den virker på. Så arbeidet er minimalt.
Dette stemmer overens med det som ble sagt i begynnelsen: Hvis arbeidet er positivt, tilføres energi til systemet, og hvis det er negativt, trekker det fra.
Nettverk Wnett Det er definert som summen av arbeidet som er utført av alle kreftene som virker på systemet:
Wnett = ∑WJeg
Da kan vi konkludere med at for å garantere eksistensen av netto mekanisk arbeid er det nødvendig at:
-Eksterne krefter virker på objektet.
-Disse kreftene er ikke alle vinkelrette på forskyvningen (cos θ ≠ 0).
-Jobbene utført av hver styrke avbryter ikke hverandre.
-Det er en forskyvning.
Eksempler på mekanisk arbeid
-Når det er nødvendig å sette en gjenstand i bevegelse fra hvile, er det nødvendig å utføre mekanisk arbeid. For eksempel skyve et kjøleskap eller en tung koffert på en horisontal overflate.
-Et annet eksempel på en situasjon der du trenger å gjøre mekanisk arbeid er å endre hastigheten på en ball som beveger seg..
-Det kreves arbeid for å heve en gjenstand til en viss høyde over gulvet.
Nå er det like vanlige situasjoner der ikke arbeidet blir gjort, selv om utseendet tilsier noe annet. Vi har sagt at for å løfte en gjenstand til en viss høyde må du utføre arbeid, så vi bærer gjenstanden, løfter den over hodet og holder den der. Gjør vi arbeid?
Tilsynelatende ja, for hvis gjenstanden er tung, vil armene dekkes på kort tid, men uansett hvor vanskelig det er, blir det ikke gjort noe arbeid fra fysikkens synspunkt. Hvorfor ikke? Vel fordi objektet ikke beveger seg.
Et annet tilfelle der, til tross for at den har en ytre kraft, ikke utfører mekanisk arbeid, er når partikkelen har en jevn sirkelbevegelse.
For eksempel et barn som snurrer en stein bundet til en streng. Strengspenningen er den sentripetale kraften som lar steinen rotere. Men til enhver tid er denne kraften vinkelrett på forskyvningen. Da utfører han ikke mekanisk arbeid, selv om det favoriserer bevegelse.
The work-kinetic energy theorem
Systemets kinetiske energi er den som den har i kraft av sin bevegelse. Ja m er massen og v er bevegelseshastigheten, er den kinetiske energien betegnet med K og er gitt av:
K = ½ mvto
Per definisjon kan ikke den kinetiske energien til et objekt være negativ, siden både massen og kvadratet av hastigheten alltid er positive størrelser. Den kinetiske energien kan være 0 når objektet er i ro.
For å endre kinetisk energi til et system, er det nødvendig å variere hastigheten - vi vil vurdere at massen forblir konstant, selv om dette ikke alltid er tilfelle. Dette krever netto arbeid på systemet, derfor:
Wnett = ΔK
Dette er arbeidet - kinetisk energisetning. Det heter at:
Netto arbeid er lik endringen i systemets kinetiske energi
Merk at selv om K alltid er positiv, kan ΔK være positiv eller negativ, siden:
ΔK = Kendelig - K første
Ja Kendelig >K første systemet har fått energi og ΔK> 0. Tvert imot, hvis Kendelig < K første, systemet har gitt opp strøm.
Arbeidet er gjort for å strekke en fjær
Når en fjær er strukket (eller komprimert), må arbeidet utføres. Dette arbeidet lagres om våren, slik at dette igjen kan arbeide med for eksempel en blokk som er festet til den ene enden..
Hookes lov sier at styrken som utøves av en fjær er en gjenopprettende kraft - den er i strid med forskyvning - og også proporsjonal med nevnte forskyvning. Konstanten av proporsjonaliteten avhenger av hvordan fjæren er: myk og lett deformerbar eller stiv.
Denne kraften er gitt av:
Fr = -kx
I uttrykket, Fr er styrken, k er våren konstant og x er forskyvningen. Det negative tegnet indikerer at kraften som utøves av fjæren motarbeider forskyvningen.
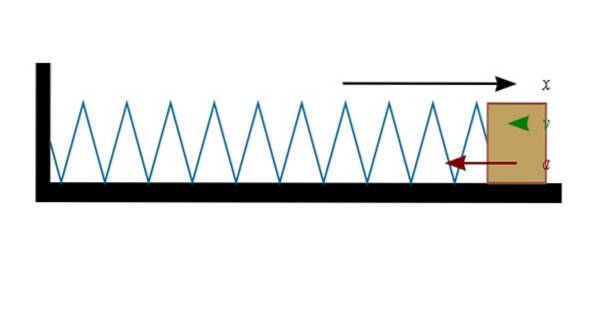
Hvis fjæren er komprimert (til venstre i figuren), vil blokken i enden bevege seg mot høyre. Og når fjæren er strukket (til høyre), vil blokken bevege seg mot venstre.
For å komprimere eller strekke fjæren, må en ekstern agent utføre arbeidet, og siden det er en variabel kraft, for å beregne det nevnte arbeidet, må vi bruke definisjonen gitt i begynnelsen:
Det er veldig viktig å merke seg at dette er arbeidet som gjøres av den eksterne agenten (for eksempel en persons hånd) for å komprimere eller strekke fjæren. Derfor vises ikke det negative tegnet. Og siden posisjonene er kvadratiske, spiller det ingen rolle om de er kompresjoner eller strekninger..
Arbeidet som våren igjen vil gjøre på blokken er:
Wvår = -Wekst
Opplæring
Øvelse 1
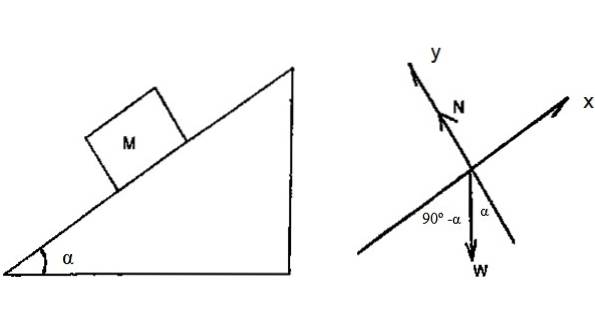
Blokken i figur 4 har masse M = 2 kg og glir nedover det skråplanet uten friksjon, med α = 36,9º. Forutsatt at det er lov å skyve fra hvile fra toppen av planet, hvis høyde er h = 3 m, finn hastigheten som blokken når bunnen av planet ved å bruke arbeidskinetisk energisetning.

Løsning
Frikroppsdiagrammet viser at den eneste kraften som er i stand til å utføre arbeid på blokken, er vekt. Mer nøyaktig: vektkomponenten langs x-aksen.
Avstanden som ble reist av blokken på planet, beregnes ved hjelp av trigonometri:
d = 3 / (cos 36,9º) m = 3,75 m
Wvekt = (Mg). d. cos (90-α) = 2 x 9,8 x 3,75 x cos 53,1 º J = 44,1 J
Etter arbeidskinetisk energisetning:
Wnett = ΔK
Wnett = Wvekt
ΔK = ½ MvFto- ½ Mvellerto
Siden den er frigjort fra hvile, veller = 0, Og dermed:
Wnett = ½ MvFto

Øvelse 2
En horisontal fjær, hvis konstant er k = 750 N / m, er festet i den ene enden til en vegg. En person komprimerer den andre enden en avstand på 5 cm. Beregn: a) Kraften som utøves av personen, b) Arbeidet han gjorde for å komprimere fjæren.
Løsning
a) Størrelsen på kraften som påføres av personen er:
F = kx = 750 N / m. 5x10 -to m = 37,5 N.
b) Hvis enden av våren opprinnelig er på x1 = 0, for å ta det derfra til endelig posisjon xto = 5 cm, er det nødvendig å gjøre følgende arbeid, i henhold til resultatet oppnådd i forrige avsnitt:
Wekst = ½ k (xtoto - x1to) = 0,5 x 750 x (0,05to -0to) J = 0,9375 J.
Referanser
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volum 2. Dynamikk. Redigert av Douglas Figueroa (USB).
- Iparraguirre, L. 2009. Grunnleggende mekanikk. Samfunnsvitenskap og matematikk. Gratis distribusjon på nettet.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Fysikk Libretexts. Sats på arbeidsenergi. Gjenopprettet fra: phys.libretexts.org
- Arbeid og energi. Gjenopprettet fra: physics.bu.edu
- Arbeid, energi og kraft. Hentet fra: ncert.nic.in



Ingen har kommentert denne artikkelen ennå.