
Isosceles trekant egenskaper, formel og areal, beregning

EN likebent trekant er en polygon med tre sider, hvor to av dem har samme mål og den tredje siden et annet mål. Denne siste siden kalles basen. På grunn av denne karakteristikken ble det gitt dette navnet, som på gresk betyr "like ben"
Trekanter er polygoner som betraktes som de enkleste i geometri, fordi de består av tre sider, tre vinkler og tre hjørner. Det er de som har minst antall sider og vinkler i forhold til de andre polygonene, men bruken er veldig omfattende.

Artikkelindeks
- 1 Egenskaper for likebenede trekanter
- 1.1 Komponenter
- 2 eiendommer
- 2.1 Innvendige vinkler
- 2.2 Summen av sidene
- 2.3 Kongruente sider
- 2.4 Kongruente vinkler
- 2.5 Høyde, median, halvering og halvering er sammenfallende
- 2.6 Relative høyder
- 2.7 Sammenfallende ortosenter, barycenter, incenter og circumcenter
- 3 Hvordan beregne omkretsen?
- 4 Hvordan beregne høyden?
- 5 Hvordan beregne arealet?
- 6 Hvordan beregne trekanten?
- 7 Øvelser
- 7.1 Første øvelse
- 7.2 Andre øvelse
- 7.3 Tredje øvelse
- 8 Referanser
Kjennetegn på likebenede trekanter
Den likestilte trekanten ble klassifisert ved hjelp av målene på sidene som en parameter, siden to av sidene er kongruente (de har samme lengde).
Basert på amplituden til de innvendige vinklene, er likebenede trekanter klassifisert som:
- Isosceles høyre trekant: to av sidene er like. En av vinklene er riktig (90eller) og de andre er de samme (45eller Hver)
- Isosceles stump trekant: to av sidene er like. En av vinklene er stump (> 90eller).
- Isosceles akutt trekant: to av sidene er like. Alle vinklene er spisse (< 90eller), der to har samme mål.
Komponenter (rediger)
- Median: er en linje som starter fra midtpunktet til den ene siden og når motsatt toppunkt. De tre medianene konvergerer på et punkt som kalles barycenter eller centroid..
- Bisektor: er en stråle som deler vinkelen på hvert toppunkt i to like vinkler. Det er derfor det er kjent som symmetriaksen, og denne typen trekanter har bare en.
- Mediatrisen: er et segment vinkelrett på siden av trekanten, som har sitt utspring i midten av trekanten. Det er tre medikamenter i en trekant, og de møtes på et punkt som kalles circumcenter.
- Høyden: er linjen som går fra toppunktet til den motsatte siden, og også denne linjen er vinkelrett på den siden. Alle trekanter har tre høyder, som sammenfaller på et punkt som kalles ortosenteret..
Eiendommer
Isosceles trekanter defineres eller identifiseres fordi de har flere egenskaper som representerer dem, med utgangspunkt i teoremene foreslått av store matematikere:
Innvendige vinkler
Summen av innvendige vinkler er alltid lik 180eller.
Summen av sidene
Summen av målene fra to sider må alltid være større enn målene for den tredje siden, a + b> c.
Kongruente sider
Ensartede trekanter har to sider med samme mål eller lengde; det vil si at de er kongruente og den tredje siden er forskjellig fra disse.
Kongruente vinkler
Isosceles trekanter er også kjent som isoangle trekanter, fordi de har to vinkler som har samme mål (kongruent). Disse er plassert i bunnen av trekanten, motsatt sidene som har samme lengde.
På grunn av dette ble teoremet generert som sier at:
"Hvis en trekant har to kongruente sider, vil også vinklene overfor disse sidene være kongruente." Derfor, hvis en trekant er likbenet, er vinklene på basene kongruente.
Eksempel:
Følgende figur viser en trekant ABC. Ved å tegne halveringen fra toppunktet til vinkel B til basen, er trekanten delt inn i to like trekanter BDA og BDC:
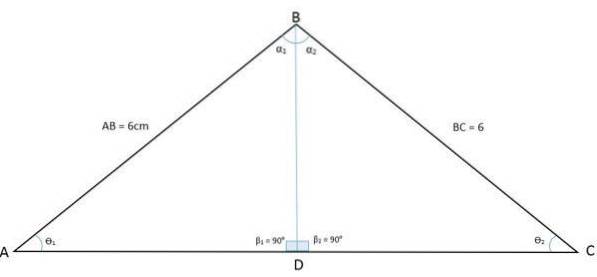
På denne måten ble vinkelen på toppunkt B også delt inn i to like vinkler. Halveringslinjen er nå den vanlige siden (BD) mellom de to nye trekanter, mens sidene AB og BC er de kongruente sidene. Dermed har vi tilfellet med kongruensside, vinkel, side (LAL).
Dette viser at vinklene til toppunktene A og C har samme mål, samt at det kan vises at siden trekantene BDA og BDC er kongruente, er sidene AD og DC også kongruente..
Høyde, median, halvering og halvering er sammenfallende
Linjen som er tegnet fra toppunktet motsatt basen til midtpunktet til basen av den likestilte trekanten, er samtidig høyden, medianen og halveringslinjen, så vel som halveringslinjen i forhold til den motsatte vinkelen til basen..
Alle disse segmentene faller sammen i en som representerer dem.
Eksempel:
Følgende figur viser trekanten ABC med et midtpunkt M som deler basen i to segmenter BM og CM.
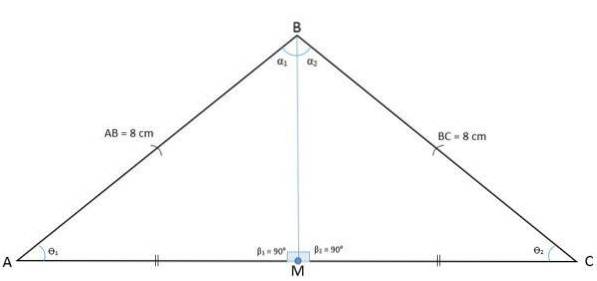
Ved å tegne et segment fra punkt M til motsatt toppunkt, oppnås per definisjon medianen AM, som er relativt til toppunkt A og side BC.
Når segmentet AM deler trekanten ABC i to like store trekanter AMB og AMC, betyr det at tilfellet med kongruensside, vinkel, side vil bli hatt, og derfor vil AM også være halveringspunktet til BÂC.
Derfor vil halveringslinjen alltid være lik medianen og omvendt..
Segmentet AM danner vinkler som har samme mål for trekantene AMB og AMC; det vil si at de er supplerende på en slik måte at målet for hver enkelt vil være:
Med. (AMB) + Med. (AMC) = 180eller
to * Med. (AMC) = 180eller
Med. (AMC) = 180eller ÷ 2
Med. (AMC) = 90eller
Det kan være kjent at vinklene dannet av segment AM i forhold til bunnen av trekanten er rette, noe som indikerer at dette segmentet er helt vinkelrett på basen..
Representerer derfor høyden og halveringen, vel vitende om at M er midtpunktet.
Derfor linjen AM:
- Representerer på høyden av f.Kr..
- Er middels størrelse.
- Den er inneholdt i halvsnittet av BC.
- Det er halveringspunktet i toppunktvinkelen Â
Relative høyder
Høyder som er relative til like sider har også samme måling.
Siden den likestilte trekanten har to like sider, vil deres to respektive høyder også være like..
Ortocenter, barycenter, incenter og sammenfallende circumcenter
Ettersom høyden, medianen, halveringen og halveringen i forhold til basen, er representert samtidig av det samme segmentet, vil ortosenteret, sentrumsbarynsenteret og omløpssentralen være kollinære punkter, det vil si at de vil være på samme linje:

Hvordan beregne omkretsen?
Omkretsen til en polygon beregnes ved å legge til sidene.
Som i dette tilfellet den likebenede trekanten har to sider med samme mål, blir omkretsen beregnet med følgende formel:
P = 2*(side a) + (side b).
Hvordan beregne høyden?
Høyden er linjen vinkelrett på basen, den deler trekanten i to like store deler når den strekker seg til motsatt toppunkt.
Høyden representerer det motsatte benet (a), midten av basen (b / 2) det tilstøtende benet og siden "a" representerer hypotenusen.
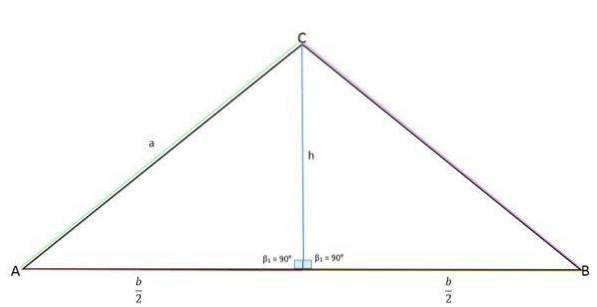
Ved hjelp av Pythagoras teorem kan verdien av høyden bestemmes:
tilto + bto = cto
Hvor:
tilto = høyde (h).
bto = b / 2.
cto = side a.
Ved å erstatte disse verdiene i Pythagoras teorem, og løse høyden, har vi:
hto + (b / to)to = tilto
hto + bto / 4 = tilto
hto = tilto - bto / 4
h = √ (tilto - bto / 4).
Hvis vinkelen som er dannet av de kongruente sidene er kjent, kan høyden beregnes med følgende formel:

Hvordan beregne arealet?
Arealet til trekantene beregnes alltid med samme formel, multipliserer basis ganger høyden og deler med to:

Det er tilfeller der bare målingene av to sider av trekanten og vinkelen som er dannet mellom dem er kjent. I dette tilfellet er det nødvendig å bruke de trigonometriske forholdene for å bestemme området:
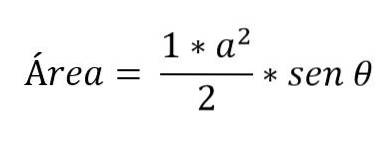
Hvordan beregne trekanten?
Siden den likestilte trekanten har to like sider, er det nødvendig å vite minst høyden eller en av vinklene for å bestemme verdien av basen..
Å kjenne høyden, brukes den pythagoreiske teoremet:
tilto + bto = cto
Hvor:
tilto = høyde (h).
cto = side a.
bto = b / 2, er ukjent.
Vi løser for bto av formelen, og vi må:
bto = ato - cto
b = √ ato - cto
Siden denne verdien tilsvarer halvparten av basen, må den multipliseres med to for å få fullstendig mål for basen til den likebenede trekanten:
b = 2 * (√ ato - cto)
I tilfelle at bare verdien av de like sidene og vinkelen mellom dem er kjent, brukes trigonometri, og tegner en linje fra toppunktet til basen som deler den likestilte trekanten i to høyre trekanter.
På denne måten beregnes halvparten av basen med:

Det er også mulig at bare verdien av høyden og vinkelen på toppunktet som er overfor basen er kjent. I så fall, ved trigonometri, kan basen bestemmes:

Opplæring
Første øvelse
Finn området av den likebenede trekanten ABC, og vit at to av sidene er 10 cm og den tredje siden er 12 cm.
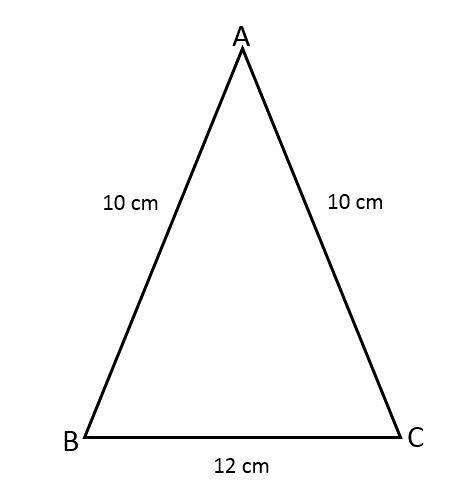
Løsning
For å finne arealet av trekanten er det nødvendig å beregne høyden ved hjelp av arealformelen som er relatert til Pythagoras teorem, siden verdien av vinkelen som er dannet mellom de like sidene ikke er kjent.
Vi har følgende data om den likebenede trekanten:
- Like sider (a) = 10 cm.
- Base (b) = 12 cm.
Verdiene er substituert i formelen:

Andre øvelse
Lengden på de to like sidene av en likestilt trekant er 42 cm, foreningen av disse sidene danner en vinkel på 130eller. Bestem verdien av den tredje siden, området til den trekanten og omkretsen.
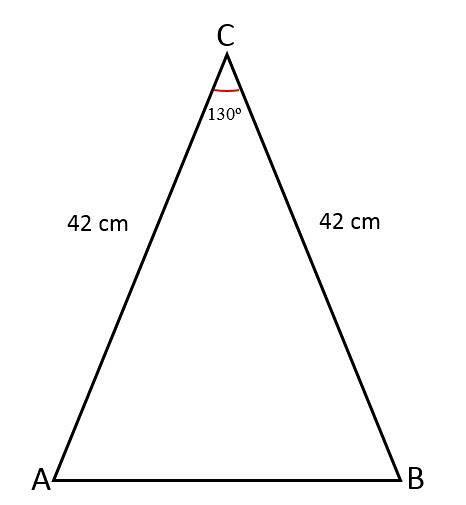
Løsning
I dette tilfellet er målene på sidene og vinkelen mellom dem kjent..
For å vite verdien av den manglende siden, det vil si basen til den trekanten, tegnes en linje vinkelrett på den, som deler vinkelen i to like deler, en for hver høyre trekant som dannes.
- Like sider (a) = 42 cm.
- Vinkel (Ɵ) = 130eller
Nå ved trigonometri beregnes verdien av halvparten av basen, som tilsvarer halvparten av hypotenusen:
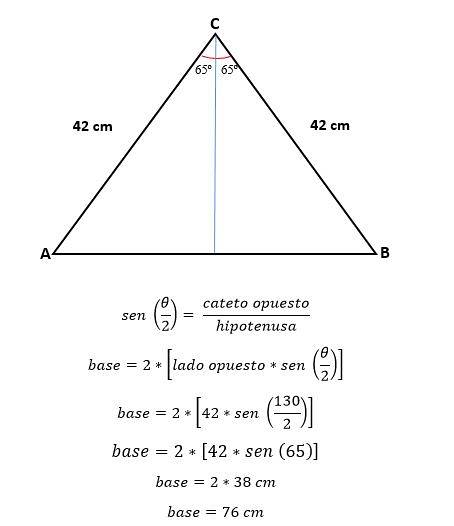
For å beregne arealet er det nødvendig å kjenne høyden på den trekanten som kan beregnes ved hjelp av trigonometri eller av Pythagoras teorem, nå som verdien av basen allerede er bestemt.
Ved trigonometri vil det være:

Perimeteren beregnes:
P = 2*(side a) + (side b).
P = 2* (42 cm) + (76 cm)
P = 84 cm + 76 cm
P = 160 cm.
Tredje øvelse
Beregn de indre vinklene til den likebenede trekanten, vel vitende om at vinkelen på basen er  = 55eller
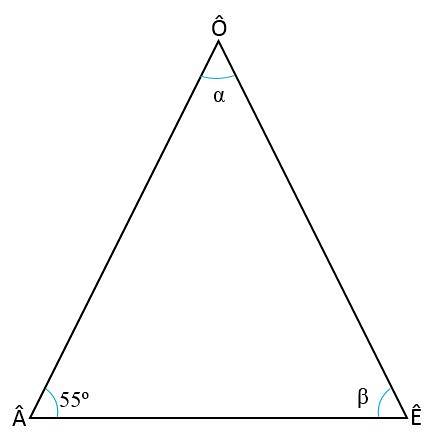
Løsning
For å finne de to manglende vinklene (Ê og Ô) er det nødvendig å huske to egenskaper til trekanter:
- Summen av innvendige vinkler i hver trekant vil alltid være = 180eller:
 + Ê + Ô = 180 eller
- I en likestilt trekant er vinklene på basen alltid kongruente, det vil si at de har samme mål, derfor:
 = Ô
Ê = 55eller
For å bestemme verdien av vinkelen Ê, erstatter vi verdiene til de andre vinklene i den første regelen og løser for Ê:
55eller + 55eller + Ô = 180 eller
110 eller + Ô = 180 eller
Ô = 180 eller - 110 eller
Ô = 70 eller.
Referanser
- Álvarez, E. (2003). Element av geometri: med mange øvelser og kompass geometri. University of Medellin.
- Álvaro Rendón, A. R. (2004). Teknisk tegning: aktivitetsbok.
- Angel, A. R. (2007). Elementær algebra. Pearson Education.
- Arthur Goodman, L. H. (1996). Algebra og trigonometri med analytisk geometri. Pearson Education.
- Baldor, A. (1941). Algebra. Havana: Kultur.
- José Jiménez, L. J. (2006). Matematikk 2.
- Tuma, J. (1998). Engineering Mathematics Handbook. Wolfram MathWorld.


Ingen har kommentert denne artikkelen ennå.