
Resulterende vektorberegning, eksempler, øvelser
De resulterende vektor er den som er oppnådd ved hjelp av en operasjon med vektorer hvis resultat også er en vektor. Normalt er denne operasjonen summen av to eller flere vektorer, ved hjelp av hvilke en vektor oppnås hvis effekt er ekvivalent.
På denne måten oppnås vektorer som den resulterende hastighet, akselerasjon eller kraft. For eksempel når flere krefter virker på en kropp F1, Fto, F3,…. vektorsummen av alle disse kreftene er ekvivalent med nettokraften (den resulterende), som matematisk uttrykkes som følger:
F1 + Fto + F3 +... = FR eller FN

Den resulterende vektoren, enten det er krefter eller en hvilken som helst annen vektorstørrelse, blir funnet ved å bruke reglene for vektortilsetning. Ettersom vektorene har retning og sans i tillegg til numerisk verdi, er det ikke nok å legge til modulene for å ha den resulterende vektoren.
Dette gjelder bare i tilfelle der vektorene som er involvert er i samme retning (se eksempler). Ellers er det nødvendig å bruke vektorsummemetoder, som avhengig av tilfelle kan være geometriske eller analytiske..
Artikkelindeks
- 1 Eksempler
- 1.1 Geometriske metoder for å legge til to vektorer
- 2 Øvelser
- 2.1-Øvelse 1
- 2.2 Øvelse 2
- 3 Referanser
Eksempler
De geometriske metodene for å finne den resulterende vektoren er den polygonale metoden og parallellogrammetoden.
Når det gjelder analytiske metoder, er det komponentmetoden, ved hvilken vektoren som kommer fra ethvert vektor-system kan bli funnet, forutsatt at vi har dens kartesiske komponenter..
Geometriske metoder for å legge til to vektorer
Anta vektorene eller Y v (Vi betegner dem med fet skrift for å skille dem fra skalarene). I figur 2a) har vi dem plassert på flyet. I figur 2 b) er den overført til vektoren v på en slik måte at dens opprinnelse sammenfaller med slutten av eller. Den resulterende vektoren kommer fra opprinnelsen til den første (eller) til toppen av den siste (v):
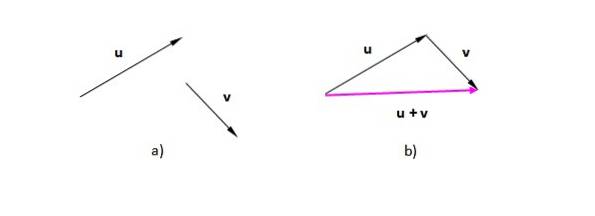
Den resulterende figuren i dette tilfellet er en trekant (en trekant er en 3-sidig polygon). Hvis vi har to vektorer i samme retning, er prosedyren den samme: plasser en av vektorene etter den andre og tegne en som går fra opprinnelsen eller halen til den første til spissen eller enden av den siste.
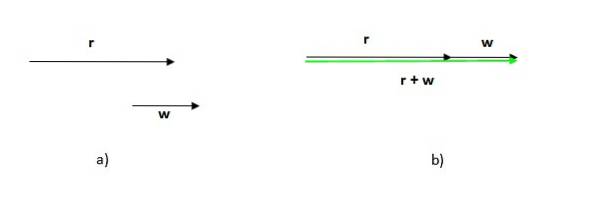
Merk at rekkefølgen denne prosedyren er gjort, ikke betyr noe, siden summen av vektorer er kommutativ.
Vær også oppmerksom på at i dette tilfellet modul (lengden eller størrelsen) på den resulterende vektoren er summen av modulene til de tilførte vektorene, i motsetning til det forrige tilfellet, der modulen til den resulterende vektoren er mindre enn summen av modulene til deltakerne.
Parallelogrammetode
Denne metoden er veldig hensiktsmessig når du trenger å legge til to vektorer hvis opprinnelsespunkter sammenfaller, for eksempel med opprinnelsen til et x-y koordinatsystem. Anta at dette er tilfelle for vektorene våre eller Y v (figur 3a):
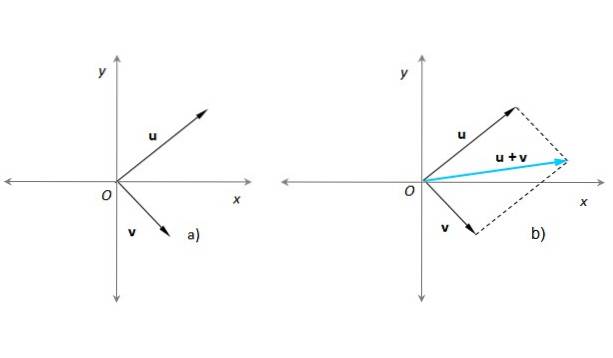
I figur 3b er det konstruert et parallellogram ved hjelp av stiplede linjer parallelt med eller allerede v. Den resulterende vektoren har sin opprinnelse ved O og slutten på punktet der de stiplede linjene krysser hverandre. Denne prosedyren tilsvarer den som er beskrevet i forrige avsnitt..
Opplæring
-Øvelse 1
Gitt følgende vektorer, finn den resulterende vektoren ved hjelp av traversmetoden.
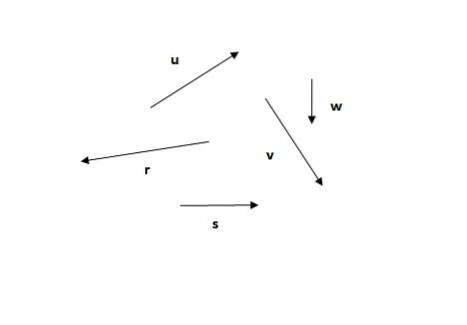
Løsning
Traversemetoden er den første av metodene som er sett. Husk at summen av vektorer er kommutativ (rekkefølgen på tilleggene endrer ikke summen), så du kan starte med hvilken som helst av vektorene, for eksempel eller (figur 5a) eller r (figur 5b):
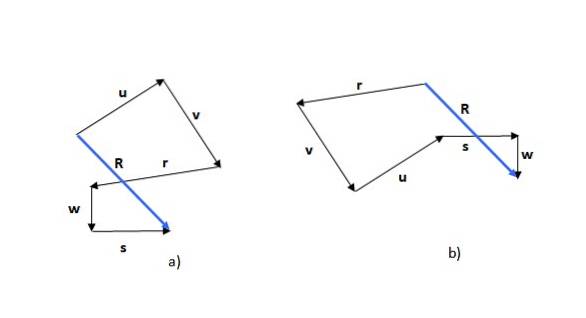
Figuren som er oppnådd er en polygon, og den resulterende vektoren (i blått) kalles R. Hvis du begynner med en annen vektor, kan formen som dannes være forskjellig, som du kan se i eksemplet, men den resulterende vektoren er den samme.
Øvelse 2
I den følgende figuren er det kjent at modulene til vektorene eller Y v henholdsvis er de u = 3 vilkårlige enheter og v = 1,8 vilkårlige enheter. Vinkelen som eller form med den positive x-aksen er 45º, mens v den danner 60º med y-aksen, som vist på figuren. Finn den resulterende vektoren, størrelsen og retningen.
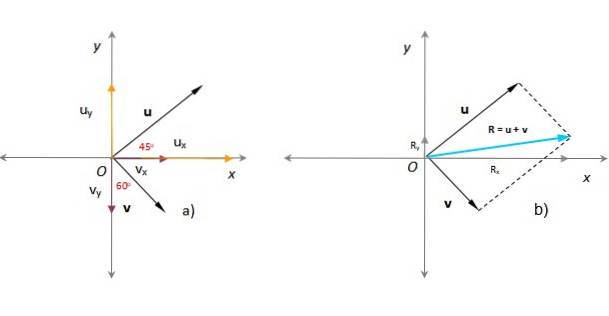
Løsning
I forrige avsnitt ble den resulterende vektoren funnet ved å bruke parallellogrammetoden (i turkis på figuren).
En enkel måte å finne den resulterende vektoren analytisk er å uttrykke tilleggsvektorene i form av deres kartesiske komponenter, noe som er enkelt når modulus og vinkel er kjent, slik som vektorene i dette eksemplet:
ellerx = u. cos 45º = 3 x cos 45º = 2.12; ellerY = u. sin 45º = 3x sin 45º = 2.12
vx = v. sin 60º = 1,8 x sin 60º = 1,56; vY = -v. cos 60º = -1,8 x cos 60º = - 0,9
Vektorer eller Y v de er vektorer som tilhører flyet, og har derfor to komponenter hver. Vektor u er i første kvadrant og komponentene er positive, mens vektor v er i fjerde kvadrant; dens x-komponent er positiv, men projeksjonen på den vertikale aksen faller på den negative y-aksen.
Beregning av de kartesiske komponentene i den resulterende vektoren
Den resulterende vektoren blir funnet ved å legge algebraisk til de respektive x- og y-komponentene for å oppnå deres kartesiske komponenter:
Rx = 2,12 + 1,56 = 3,68
RY = 2,12 + (-0,9) = 1,22
Når kartesiske komponenter er spesifisert, er vektoren fullstendig kjent. Den resulterende vektoren kan uttrykkes med notasjonen i firkantede parenteser (seler):
R = < 3.68; 1.22> vilkårlige enheter
Notasjonen med firkantede parenteser brukes til å skille en vektor fra et punkt i planet (eller i rommet). En annen måte å uttrykke den resulterende vektoren analytisk på er å bruke enhetsvektorene Jeg og j i flyet (Jeg, j Y k i rommet):
R = 3,68 Jeg + 1.22 j vilkårlige enheter
Siden begge komponentene i den resulterende vektoren er positive, er vektoren R tilhører den første kvadranten, som allerede hadde blitt sett grafisk før.
Størrelse og retning av den resulterende vektoren
Å kjenne de kartesiske komponentene, beregnes størrelsen på R gjennom Pythagoras teorem, siden den resulterende vektoren R, sammen med R-komponentenex og RY danne en rett trekant:
Størrelse eller modul: R = (3.68to + 1.22to)½ = 3,88
Retning q tar den positive x-aksen som referanse: q = arctan (RY / Rx) = arctg (1.22 /3.68) = 18.3 º
Referanser
- Legge til vektorer og regler. Hentet fra: newt.phys.unsw.edu.au
- Figueroa, D. Series: Physics for Sciences and Engineering. Volum 1. Kinematikk. 31-68.
- Fysisk. Modul 8: Vektorer. Gjenopprettet fra: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mekanikk for ingeniører. Statisk. 6. utgave. Continental Publishing Company. 15-53.
- Vector Addition Calculator. Hentet fra: www.1728.org



Ingen har kommentert denne artikkelen ennå.