De øyeblikkelig akselerasjon Det er endringen som hastigheten opplever per tidsenhet i hvert øyeblikk av bevegelsen. I det nøyaktige øyeblikket da “dragster”Av bildet som ble fotografert, hadde det en akselerasjon på 29,4 m / sto. Dette betyr at hastigheten på den tiden ble økt med 29,4 m / s i løpet av 1 s. Dette tilsvarer 105 km / t på bare 1 sekund.
En dragster-konkurranse er lett modellert forutsatt at racerbilen er et punktobjekt. P som beveger seg i en rett linje. På denne linjen velges en akse orientert med opprinnelse ELLER at vi vil kalle aksenOKSE) eller bare akse x.
De kinematiske variablene som definerer og beskriver bevegelsen er:
De er alle vektormengder. Derfor har de en styrke, en retning og en sans.
Når det gjelder rettlinjet bevegelse, er det bare to mulige retninger: positiv (+) i retning av (OKSE) eller negativ (-) i motsatt retning av (OKSE). Derfor er det mulig å dispensere med den formelle vektornotasjonen og bruke tegnene for å indikere følelsen av størrelsen.
Artikkelindeks
Anta det for øyeblikket t partikkelen har hastighet v (t) og i øyeblikket t ' hastigheten er v (t ').
Så endringen som farten hadde i den perioden var Δv = v (t ') - v (t). Derfor akselerasjonen i tidsforløpet Δt = t '- t , vil bli gitt av kvotienten:
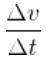
Denne kvoten er den gjennomsnittlige akselerasjonen vedm i tidsperioden Δt mellom øyeblikkene t og t '.
Hvis vi ønsket å beregne akselerasjonen akkurat på tidspunktet t, bør t 'være en ubetydelig større mengde enn t. Med dette Δt, som er forskjellen mellom de to, skal det være nesten null.
Matematisk er det indikert som følger: Δt → 0 og det oppnås:
JEG) En partikkel beveger seg langs X-aksen med konstant hastighet v0 = 3 m / s. Hva blir akselerasjonen av partikkelen?
Derivatet av en konstant er null, derfor er akselerasjonen til en partikkel som beveger seg med konstant hastighet null.
II) En partikkel beveger seg på aksen x og hastigheten endres med tiden i henhold til følgende formel:
v (t) = 2-3 t
Hvor hastighet måles i m / s og tid i s. Hva blir akselerasjonen av partikkelen?
)
Resultatet tolkes slik: for hvert øyeblikk er akselerasjonen -3 m / s.
Mellom øyeblikkene 0 s og 2/3 s er hastigheten positiv mens akselerasjonen er negativ, det vil si i det intervallet reduserer partikkelen sin hastighet eller reduserer.
I øyeblikket 2/3 s blir hastigheten null, men da det gjenstår en akselerasjon på -3 m / s, snur hastigheten fra det øyeblikket (den blir negativ).
I øyeblikkene etter ⅔ s akselererer partikkelen, siden hver gang hastigheten blir mer negativ, det vil si at hastigheten (hastighetsmodulen) vokser.
III) Figuren viser en kurve som representerer hastigheten som en funksjon av tiden for en partikkel som beveger seg langs X-aksen. Finn tegnet på akselerasjonen til tider t1, tto og du3. Angi også om partikkelen akselererer eller bremser.
Akselerasjon er avledet av hastighetsfunksjonen, og tilsvarer derfor hellingen til tangentlinjen til kurven v (t) for et gitt øyeblikk.
For øyeblikket t1, skråningen er negativ, så akselerasjonen er negativ. Og siden det øyeblikket hastigheten er positiv, kan vi bekrefte at partikkelen i det øyeblikket avtar.
For øyeblikket tto tangenslinjen til kurven v (t) er vannrett, så hellingen er null. Mobilen har null akselerasjon, derfor på tto partikelen verken akselererer eller bremser.
For øyeblikket t3, hellingen til tangentlinjen til kurven v (t) er positiv. Med en positiv akselerasjon akselererer partikkelen virkelig, for i det øyeblikket er også hastigheten positiv.
I forrige avsnitt ble øyeblikkelig akselerasjon definert fra øyeblikkelig hastighet. Med andre ord, hvis hastigheten er kjent i hvert øyeblikk, er det også mulig å kjenne akselerasjonen i hvert øyeblikk av bevegelsen..
Den omvendte prosessen er mulig. Det vil si å vite akselerasjonen for hvert øyeblikk, så kan øyeblikkelig hastighet beregnes.
Hvis operasjonen som tillater å gå fra hastighet til akselerasjon er derivatet, er den motsatte matematiske operasjonen integrasjon.
Akselerasjonen til en partikkel som beveger seg langs X-aksen er a (t) = ¼ tto. Hvor t måles i sekunder og a i m / s. Bestem akselerasjonen og hastigheten til partikkelen ved 2 s bevegelse, vel vitende om at i det første øyeblikk t0 = 0 var i ro.
Ved 2 s er akselerasjonen 1 m / sto og hastigheten for øyeblikket t vil bli gitt av:
Et objekt beveger seg langs X-aksen med en hastighet i m / s, gitt av:
v (t) = 3 tto - 2 t, hvor t måles i sekunder. Bestem akselerasjonen til tider: 0s, 1s, 3s.
Ved å ta derivatet av v (t) med hensyn til t, oppnås akselerasjonen når som helst:
a (t) = 6t -2
Deretter er (0) = -2 m / sto ; a (1) = 4 m / sto ; a (3) = 16 m / sto .
En metallkule frigjøres fra toppen av en bygning. Fallende akselerasjon er tyngdeakselerasjonen som kan tilnærmes med verdien 10 m / s2 og peker nedover. Bestem hastigheten til sfæren 3 s etter at den er utgitt.
Dette problemet innebærer akselerasjon av tyngdekraften. Tar den vertikale retningen som positiv ned, vi har at sfærens akselerasjon er:
a (t) = 10 m / sto
Og hastigheten vil bli gitt av:
En metallkule skytes oppover med en innledende hastighet på 30 m / s. Akselerasjonen av bevegelse er tyngdeakselerasjonen som kan tilnærmes med verdien 10 m / sto og peker nedover. Bestem kulehastigheten ved 2 s og 4 s etter at den er skutt.
Den vertikale retningen vil bli tatt som positiv oppover. OGI så fall vil akselerasjonen av bevegelsen bli gitt av
a (t) = -10 m / sto
Hastigheten som en funksjon av tiden vil bli gitt av:
Etter at 4 s har blitt avfyrt, vil hastigheten være 30 - 10 ∙ 4 = -10 m / s. Noe som betyr at sfæren faller ned med en hastighet på 10 m / s ved 4 s.
Ingen har kommentert denne artikkelen ennå.